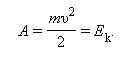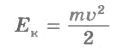|
|
|
| (2 промежуточные версии не показаны) | | Строка 7: |
Строка 7: |
| | <h2>Кинетическая энергия</h2> | | <h2>Кинетическая энергия</h2> |
| | | | |
| - | Кинетической энергией называется такая энергия, которой тело обладает вследствие своего движения.
| + | Кинетическая энергия - это энергия тела, которую оно имеет вследствие своего движения. |
| | | | |
| - | Если говорить простым языком, то под понятием кинетической энергии следует подразумевать только ту энергию, которую имеет тело при движении. Если же тело находится в состоянии покоя, то есть, совершенно не движется, то в этом случае кинетическая энергия равна нулю. | + | Если говорить простым языком, то под понятием кинетической энергии следует подразумевать только ту энергию, которую имеет тело при движении. Если же тело пребывает в состоянии покоя, то есть, совершенно не движется, тогда кинетическая энергия будет равняться нулю. |
| | | | |
| | Кинетическая энергия равняется той работе, которую она должна затратить, чтобы вывести тело из состояния покоя в состояние движения с какой-то скоростью. | | Кинетическая энергия равняется той работе, которую она должна затратить, чтобы вывести тело из состояния покоя в состояние движения с какой-то скоростью. |
| | | | |
| - | Таким образом кинетическая энергия является разностью между полной энергией системы и её энергией покоя. Другими словами можно сказать, что кинетическая энергия - это часть полной энергии, обусловленная движением.
| + | Следовательно, кинетическая энергия является разностью между полной энергией системы и её энергией покоя. Иначе говоря, что кинетическая энергия будет частью полной энергии, которая обусловленная движением. |
| | | | |
| - | Давайте попробуем разобраться в понятии кинетической энергии тела. На примере движения шайбы по льду, попробуем понять связь между величиной кинетической энергии и работой, которую нужно совершить, чтобы вывести шайбу из состояния покоя и привести ее в движение, имеющее некоторую скорость. | + | Давайте попробуем разобраться в понятии кинетической энергии тела. Для примера возьмем движение шайбы по льду и попробуем понять связь между величиной кинетической энергии и работой, которая должна быть выполнена, чтобы вывести шайбу из состояния покоя и привести ее в движение, имеющее некоторую скорость. |
| | | | |
| | '''Пример''' | | '''Пример''' |
| | | | |
| - | Играющий на льду хоккеист, ударив клюшкой по шайбе сообщает ей скорость, а следовательно и кинетическую энергию. Сразу после удара клюшкой, шайба начинает очень быстрое движение, но постепенно ее скорость замедляется и наконец, она совсем останавливается. Это говорит о том, что уменьшение скорости явилось результатом силы трения, происходящей между поверхностью и шайбой. В этом случае сила трения направлена против движения и действия этой силы сопровождаются перемещением. Тело же использует имеющую механическую энергию, совершая работу против силы трения. | + | Играющий на льду хоккеист, ударив клюшкой по шайбе сообщает ей скорость, а так и кинетическую энергию. Сразу после удара клюшкой, шайба начинает очень быстрое движение, но постепенно ее скорость замедляется и наконец, она совсем останавливается. Это значит, что уменьшение скорости явилось результатом силы трения, происходящей между поверхностью и шайбой. Тогда сила трения будет направлена против движения и действия этой силы сопровождаются перемещением. Тело же использует имеющую механическую энергию, выполняя работу против силы трения. |
| | | | |
| - | Из этого примера мы видим, что кинетическая энергия является той энергией, которую получает тело вследствие своего движения. | + | Из этого примера мы видим, что кинетическая энергия будет той энергией, которую тело получает в результате своего движения. |
| | | | |
| - | Отсюда следует, что кинетическая энергия тела, которая имеет определенную массу, движется со скоростью равной той работе, которую должна совершить сила, приложенная к покоящемуся телу, чтобы сообщить ему эту скорость:
| + | Следовательно, кинетическая энергия тела, имеющая определенную массу, будет двигаться со скоростью равной той работе, которую должна выполнить сила, приложенная к покоящемуся телу, чтобы сообщить ему данную скорость: |
| | | | |
| | <br> | | <br> |
| - | [[Image:10klKunetika01.jpg|100x100px|кинетичекая]] | + | [[Image:10klKunetika01.jpg|150x150px|кинетичекая]] |
| | <br> | | <br> |
| | | | |
| Строка 32: |
Строка 32: |
| | | | |
| | <br> | | <br> |
| - | [[Image:10klKunetika02.jpg|100x100px|кинетичекая]] | + | [[Image:10klKunetika02.jpg|150x150px|кинетичекая]] |
| | <br> | | <br> |
| | | | |
| Строка 39: |
Строка 39: |
| | К свойствам кинетической энергии относятся: аддитивность, инвариантность по отношению к повороту системы отсчета и сохранение. | | К свойствам кинетической энергии относятся: аддитивность, инвариантность по отношению к повороту системы отсчета и сохранение. |
| | | | |
| - | Такое свойство, как аддитивность представляет собой кинетическую энергию механической системы, которая слагается из материальных точек и равняется сумме кинетических энергий всех материальных точек, которые входят в эту систему. | + | Такое свойство, как аддитивность являет собой кинетическую энергию механической системы, которая слагается из материальных точек и будет равна сумме кинетических энергий всех материальных точек, которые входят в эту систему. |
| | | | |
| | Свойство инвариантности по отношению к повороту системы отсчета обозначает, что кинетическая энергия не зависит от положения точки и направления её скорости. Ее зависимость распространяется лишь от модуля или от квадрата её скорости. | | Свойство инвариантности по отношению к повороту системы отсчета обозначает, что кинетическая энергия не зависит от положения точки и направления её скорости. Ее зависимость распространяется лишь от модуля или от квадрата её скорости. |
| Строка 45: |
Строка 45: |
| | Свойство сохранения обозначает, что кинетическая энергия при взаимодействиях, изменяющих лишь механические характеристики системы, совершенно не изменяется. | | Свойство сохранения обозначает, что кинетическая энергия при взаимодействиях, изменяющих лишь механические характеристики системы, совершенно не изменяется. |
| | | | |
| - | Это свойство неизменно по отношению к преобразованиям Галилея. Свойства сохранения кинетической энергии и второго закона Ньютона будет вполне достаточно, чтобы вывести математическую формулу кинетической энергии.
| + | Это свойство неизменно по отношению к преобразованиям Галилея. Свойства сохранения кинетической энергии и второго закона Ньютона будет вполне достаточно, для выведения математической формулы кинетической энергии. |
| | | | |
| | <h2>Соотношение кинетической и внутренней энергии</h2> | | <h2>Соотношение кинетической и внутренней энергии</h2> |
| | | | |
| - | Но существует такая интересная дилемма, как то, что кинетическая энергия является зависимой от того, с каких позиций рассматривать эту систему. Если, например, мы берем объект, который можно рассмотреть только под микроскопом, то, как единое целое, это тело неподвижно, хотя существует и внутренняя энергия. Но в этом случае кинетическая энергия появляется только тогда, когда это тело движется, как единое целое. | + | Но существует такая интересная дилемма, как то, что кинетическая энергия может быть зависимой от того, с каких позиций рассматривать эту систему. Если, например, мы берем объект, который можно рассмотреть только под микроскопом, то, как единое целое, это тело неподвижно, хотя существует и внутренняя энергия. При таких условиях кинетическая энергия появляется только тогда, когда это тело движется, как единое целое. |
| | | | |
| | То же тело, если рассматривать на микроскопическом уровне, обладает внутренней энергией, обусловленной движением атомов и молекул, из которых оно состоит. А абсолютная температура такого тела будет пропорциональна средней кинетической энергии такого движения атомов и молекул. | | То же тело, если рассматривать на микроскопическом уровне, обладает внутренней энергией, обусловленной движением атомов и молекул, из которых оно состоит. А абсолютная температура такого тела будет пропорциональна средней кинетической энергии такого движения атомов и молекул. |
Текущая версия на 11:41, 11 июня 2015
Гипермаркет знаний>>Физика и астрономия>>Физика 10 класс>>Физика: Кинетическая энергия и ее изменение
Кинетическая энергия
Кинетическая энергия - это энергия тела, которую оно имеет вследствие своего движения.
Если говорить простым языком, то под понятием кинетической энергии следует подразумевать только ту энергию, которую имеет тело при движении. Если же тело пребывает в состоянии покоя, то есть, совершенно не движется, тогда кинетическая энергия будет равняться нулю.
Кинетическая энергия равняется той работе, которую она должна затратить, чтобы вывести тело из состояния покоя в состояние движения с какой-то скоростью.
Следовательно, кинетическая энергия является разностью между полной энергией системы и её энергией покоя. Иначе говоря, что кинетическая энергия будет частью полной энергии, которая обусловленная движением.
Давайте попробуем разобраться в понятии кинетической энергии тела. Для примера возьмем движение шайбы по льду и попробуем понять связь между величиной кинетической энергии и работой, которая должна быть выполнена, чтобы вывести шайбу из состояния покоя и привести ее в движение, имеющее некоторую скорость.
Пример
Играющий на льду хоккеист, ударив клюшкой по шайбе сообщает ей скорость, а так и кинетическую энергию. Сразу после удара клюшкой, шайба начинает очень быстрое движение, но постепенно ее скорость замедляется и наконец, она совсем останавливается. Это значит, что уменьшение скорости явилось результатом силы трения, происходящей между поверхностью и шайбой. Тогда сила трения будет направлена против движения и действия этой силы сопровождаются перемещением. Тело же использует имеющую механическую энергию, выполняя работу против силы трения.
Из этого примера мы видим, что кинетическая энергия будет той энергией, которую тело получает в результате своего движения.
Следовательно, кинетическая энергия тела, имеющая определенную массу, будет двигаться со скоростью равной той работе, которую должна выполнить сила, приложенная к покоящемуся телу, чтобы сообщить ему данную скорость:
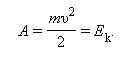
Кинетическая энергия является энергией движущегося тела, которая равняется произведению массы тела на квадрат его скорости, деленной пополам.
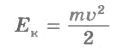
Свойства кинетической энергии
К свойствам кинетической энергии относятся: аддитивность, инвариантность по отношению к повороту системы отсчета и сохранение.
Такое свойство, как аддитивность являет собой кинетическую энергию механической системы, которая слагается из материальных точек и будет равна сумме кинетических энергий всех материальных точек, которые входят в эту систему.
Свойство инвариантности по отношению к повороту системы отсчета обозначает, что кинетическая энергия не зависит от положения точки и направления её скорости. Ее зависимость распространяется лишь от модуля или от квадрата её скорости.
Свойство сохранения обозначает, что кинетическая энергия при взаимодействиях, изменяющих лишь механические характеристики системы, совершенно не изменяется.
Это свойство неизменно по отношению к преобразованиям Галилея. Свойства сохранения кинетической энергии и второго закона Ньютона будет вполне достаточно, для выведения математической формулы кинетической энергии.
Соотношение кинетической и внутренней энергии
Но существует такая интересная дилемма, как то, что кинетическая энергия может быть зависимой от того, с каких позиций рассматривать эту систему. Если, например, мы берем объект, который можно рассмотреть только под микроскопом, то, как единое целое, это тело неподвижно, хотя существует и внутренняя энергия. При таких условиях кинетическая энергия появляется только тогда, когда это тело движется, как единое целое.
То же тело, если рассматривать на микроскопическом уровне, обладает внутренней энергией, обусловленной движением атомов и молекул, из которых оно состоит. А абсолютная температура такого тела будет пропорциональна средней кинетической энергии такого движения атомов и молекул.
|