KNOWLEDGE HYPERMARKET

Формулы корней квадратных уравнений
Строка 1: Строка 1:
-
<metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Формулы корней квадратных уравнений. квадратное уравнение, корни, теореме, функции, формулам, коэффициент, числа, знаменатель, отрицательное число, уравнение</metakeywords>  
+
'''Полужирное начертание'''<metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Формулы корней квадратных уравнений. квадратное уравнение, корни, теореме, функции, формулам, коэффициент, числа, знаменатель, отрицательное число, уравнение</metakeywords>  
'''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]&gt;&gt;[[Математика|Математика]]&gt;&gt;[[Математика 8 класс|Математика 8 класс]]&gt;&gt;Математика:Формулы корней квадратных уравнений'''<br>  
'''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]&gt;&gt;[[Математика|Математика]]&gt;&gt;[[Математика 8 класс|Математика 8 класс]]&gt;&gt;Математика:Формулы корней квадратных уравнений'''<br>  
-
<br>
+
'''Квадратные уравнения'''
-
'''Формулы корней квадратных уравнений'''
+
<h2>Определение квадратного уравнения</h2>
-
<br>Пусть дано '''[[Презентація уроку на тему "Квадратні рівняння. Теорема Вієта"|квадратное уравнение]]''' ах<sup>2 </sup>+ bх + с = 0. <br>
+
Из курса математики предыдущих классов вам уже известно, что такое уравнение, а вот какие уравнения называются квадратными, нам еще предстоит разобраться. Если вы слышите такое словосочетание, как «квадратное уравнение», то ключевым словом в этой терминологии является слово «квадратное».  
-
Применим к квадратному трехчлену ах<sup>2</sup> + bх + с те же преобразования, которые мы выполняли в § 13, когда доказывали теорему о том, что графиком функции у = ах<sup>2</sup> + bх + с является парабола. <br>
+
Ну а теперь давайте более подробно рассмотрим, как должно выглядеть квадратное уравнение. А раз оно «квадратное», то это говорит о том, что в таком уравнении обязательно должен присутствовать икс в квадрате, также может быть икс в первой степени и простое число.  Если говорить более простым языком, то в таком уравнении должен присутствовать икс, но его степень не должна быть больше двойки.
-
Имеем
+
Но, а если говорить языком математики, то это такое уравнение, которое имеет вид:
-
[[Image:13-06-15.jpg|320px|Формулы корней квадратных уравнений]]<br><br>Обычно выражение b<sup>2</sup> - 4ас обозначают буквой D и называют дискриминантом квадратного уравнения ах<sup>2</sup> + bх + с = 0 (или дискриминантом квадратного трехчлена ах + bх + с).
+
ax2 + bx + c = 0,
-
Таким образом
+
где a, b, c — некоторые числа (a ≠ 0), x — неизвестное.
-
[[Image:13-06-16.jpg|240px|Формулы корней квадратных уравнений]]<br><br>Значит, квадратное уравнение ах<sup>2</sup> + их + с = О можно переписать в виде
+
Числа, которые присутствуют в квадратном уравнении, называются коэффициентами этого квадратного уравнения:
-
[[Image:13-06-17.jpg|480px|Формулы корней квадратных уравнений]]<br><br>Любое квадратное уравнение можно преобразовать к виду (1), удобному, как мы сейчас убедимся, для того, чтобы определять число корней квадратного уравнения и находить эти '''[[Степени и корни. Степенные функции. Основные результаты|корни]]'''.  
+
• a – является первым коэффициентом квадратного уравнения;<br>
 +
• b – выступает в роли второго коэффициента;<br>
 +
• c  -  называют его свободным членом.<br>
-
[[Image:13-06-18.jpg|480px|Теорема]]<br><br>Доказательство. Если D &lt; 0, то правая часть уравнения (1) — отрицательное число; в то же время левая часть уравнения (1) при любых значениях х принимает неотрицательные значения. Значит, нет ни одного значения х, которое удовлетворяло бы уравнению (1), а потому уравнение (1) не имеет корней.
+
В общем, ясли рассматривать квадратное уравнение, которое имеет вид:
-
'''Пример 1.''' Решить уравнение 2x<sup>2</sup> + 4х + 7 = 0. <br>
+
ax2 + bx + c = 0
-
Решение. Здесь а = 2, b = 4, с = 7, D = b<sup>2</sup>-4ac = 4<sup>2</sup>'''. '''4'''. '''2'''. '''7 = 16-56 = -40. <br>
+
То мы с вами видим, что в этом квадратном уравнении с его левой стороны есть полный набор членов, где есть икс в квадрате с коэффициентом a, также икс в первой степени с коэффициентом b, ну и свободный член c.  
-
Так как D &lt; 0, то по '''[[Теорема Вієта і теорема, обернена до неї|теореме]]''' 1 данное квадратное уравнение не имеет корней.  
+
Квадратные уравнения, в котором присутствуют все три слагаемых, называются полными.  
-
[[Image:13-06-18.jpg|480px|Теорема]]<br><br>Доказательство. Если D = 0, то уравнение (1) принимает вид[[Image:13-06-19.jpg|320px|Доказательство]] &nbsp; — единственный корень уравнения.
+
Они имеют такой вид:
-
'''''Замечание 1.''''' Помните ли вы, что х = - [[Image:13-06-20.jpg]] — абсцисса вершины параболы, которая служит графиком функции у = ах<sup>2</sup> + их + с? Почему именно это значение оказалось единственным корнем квадратного уравнения ах<sup>2</sup> + их + с — 0? «Ларчик» открывается просто: если D — 0, то, как мы установили ранее,
+
<br>
 +
[[Image:8kl_kv.yravnenie01.jpg|500x500px|квадратные уравнения]]
 +
<br>  
-
[[Image:13-06-21.jpg|320px|Доказательство]]<br><br>Графиком же '''[[Предел функции|функции]]''' [[Image:13-06-22.jpg|функции]] является парабола с вершиной в точке [[Image:13-06-23.jpg|точка]] (см., например, рис. 98). Значит, абсцисса вершины параболы и единственный корень квадратного уравнения при D = 0 — одно и то же число.<br>
+
Но если, к примеру, взять коэффициент b, который равен 0, то получается, что у нас отсутствует икс в первой степени. Или же c равняется нулю, то тогда наше уравнение остается без свободного члена.
-
[[Image:13-06-24.jpg|240px|График]]
+
Из выше сказанного делаем вывод, что перед нами квадратное уравнение, у которого отсутствует коэффициент или свободный член. Такие квадратные уравнения, у которых чего-то не хватает, называются неполными квадратными уравнениями.  
-
<br>'''Пример 2.''' Решить уравнение 4x<sup>2</sup> - 20x + 25 = 0.
+
Таким образом, уравнения, у которых один из коэффициентов b  или  c  равны нулю, являются неполными квадратными уравнениями и имеют вид, например:
-
Решение. Здесь а = 4, b = -20, с = 25, D = b<sup>2</sup> - 4ас = (-20)<sup>2</sup> - 4 • 4 • 25 = 400 - 400 = 0.
+
<br>
 +
[[Image:8kl_kv.yravnenie02.jpg|500x500px|квадратные уравнения]]
 +
<br>  
-
Так как D = 0, то по теореме 2 данное квадратное уравнение имеет один корень. Этот корень находится по формуле[[Image:13-06-25.jpg|240px|Формула]] Ответ: 2,5. <br><br>'''''Замечание 2.''''' Обратите внимание, что 4х<sup>2</sup> - 20х +25 — полный квадрат: 4х<sup>2</sup> - 20х + 25 = (2х - 5)<sup>2</sup>.
+
Если же в квадратном уравнении старший коэффициент равняется единице, то такое уравнение носит название приведенного квадратного уравнения.
-
 
+
-
Если бы мы это заметили сразу, то решили бы уравнение так: (2х - 5)<sup>2</sup> = 0, значит, 2х - 5 = 0, откуда получаем х = 2,5. Вообще, если D = 0, тоах<sup>2</sup> + bх + с = [[Image:13-06-26.jpg|Формула]] — это мы отметили ранее в замечании 1. <br>Если D &gt; 0, то квадратное уравнение ах<sup>2</sup> + bх +&nbsp; с = 0 имеет два корня, которые находятся по '''[[Конспект уроку на тему «Формула коренів квадратного рівняння»|формулам]]'''
+
 +
<br>
 +
[[Image:8kl_kv.yravnenie03.jpg|500x500px|квадратные уравнения]]
<br>  
<br>  
-
[[Image:13-06-27.jpg|480px|Теорема]]<br>  
+
<h2>Способы решения квадратных уравнений</h2>
-
'''Доказательство'''. Перепишем квадратное уравнение ах<sup>2</sup> + <sup>Ь</sup>х + с = 0 в виде (1)
+
<br>
 +
[[Image:8kl_kv.yravnenie04.jpg|500x500px|квадратные уравнения]]
 +
<br>  
-
[[Image:13-06-28.jpg|120px|Уравнение]]<br><br>Положим [[Image:13-06-29.jpg|320px|Доказательство]]<br>По условию, D &gt; 0, значит, правая часть уравнения положительное число. Тогда из уравнения (2) получаем, что
+
<h2>Зачем уметь решать квадратные уравнения</h2>
-
[[Image:13-06-30.jpg|480px|Доказательство]]<br><br>Итак, заданное квадратное уравнение имеет два корня:
+
<br>
 +
[[Image:8kl_kv.yravnenie05.jpg|500x500px|квадратные уравнения]]
 +
<br>  
-
[[Image:13-06-31.jpg|420px|Доказательство]]<br>'''''<br>Замечание 3.''''' В математике довольно редко бывает так, чтобы введенный термин не имел, образно выражаясь, житейской подоплеки. Возьмем новое понятие — дискриминант. Вспомните слово «дискриминация». Что оно означает? Оно означает унижение одних и возвышение других, т.е. различное отношение к различным людям. Оба слова (и дискриминант, и дискриминация) происходят от латинского discriminans — «различающий». Дискриминант различает квадратные уравнения по числу корней.  
+
На протяжении изучения всего курса алгебры в школе, изучению уравнений отводится больше часов, чем на какие-либо другие темы по математике. А задумывались ли вы, почему так? Дело в том, что умение решать уравнения имеют не только огромное значение для досконального знания математики и естественных законов, но эти знания пригодятся вам и в практических целях.  
-
'''Пример 3.''' Решить уравнение Зх<sup>2</sup> + 8х - 11 = 0.  
+
Дело в том, что в повседневном реальном мире придется сталкиваться с различными проблемами, где никак не обойтись без решения различных видов уравнений. Научившись их решать и овладев их способами решения, в дальнейшем вы сможете легко найти ответы в любой области науки и техники.  
-
Решение. Здесь а = 3, b = 8, с = - 11, D = b<sup>2</sup> - 4ас = 8<sup>2</sup> - 4 • 3 • (-11) = 64 + 132 = 196.  
+
А умение понимать и решать квадратные уравнения, является фундаментом к освоению знаний математических наук.
-
Так как D &gt; 0, то по теореме 3 данное квадратное уравнение имеет два корня. Эти корни находятся по формулам (3)
+
<h2>История возникновения и развития квадратных уравнений</h2>
-
[[Image:13-06-32.jpg|320px|Решение]]<br><br>Фактически мы с вами выработали следующее правило:
+
Необходимость в умении решать уравнения возникла еще в глубокой древности, при этом уже тогда люди решали уравнения не только первой степени, но и второй. Это было продиктовано потребностью человека научиться вычислять площади земельных участков, а также делать шаги в развитии таких наук, как астрономия, физика, математика и т.д.
-
'''Правило решения уравнения '''<br>ах<sup>2</sup> + bх + с = 0
+
Первыми умельцами в решении квадратных уравнений можно назвать жителей Вавилона. Они их научились решать еще 4000 лет до нашей эры. Естественно, что правила решения квадратных уравнений в вавилонских текстах далеко отличались от современных, но по существу они близки. В вавилонских трактатах не было понятия отрицательного числа, да и общие методы их решения кардинально отличались.
-
[[Image:13-06-33.jpg|480px|Правило решения уравнения ]]<br><br>Это правило универсально, оно применимо как к полным, так и к неполным квадратным уравнениям. Однако неполные квадратные уравнения обычно по этому правилу не решают, их удобнее решать так, как мы это делали в предыдущем параграфе.  
+
Также пользовался решением квадратных уравнений и древнеиндийский математик Баудхаяма.  
-
'''Пример 4.''' Решить уравнения:
+
В Европе первые формулы решения этих уравнений появились лишь в 1202 г. . Они были описаны итальянским математиком Леонардом Фибоначчи в его знаменитой книге «Книге абака». 
-
а) х<sup>2</sup> + Зх - 5 = 0; &nbsp; &nbsp; &nbsp; &nbsp; &nbsp;&nbsp; б) - 9x<sup>2</sup> + 6х - 1 = 0;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; в) 2х<sup>2</sup>-х + 3,5 = 0.  
+
Немного позднее изучением этого важного математического вопроса с квадратными уравнениями занялись и такие ученые, как Ньютон, Франсуа Виет, Рене Декарт и другие выдающиеся математики.
-
Решение.
+
<h2>Применение квадратных уравнений в современной жизни</h2>
-
 
+
-
а) Здесь а = 1, b = 3, с = - 5,&nbsp; D = b<sup>2</sup> - 4ас = З<sup>2</sup> - 4 • 1 • (- 5) = 9 + 20 = 29.
+
-
 
+
-
Так как D &gt; 0, то данное квадратное уравнение имеет два корня. Эти корни находим по формулам (3)
+
-
 
+
-
[[Image:13-06-34.jpg|320px|Формулы]]<br><br>б) Как показывает опыт, удобнее иметь дело с квадратными уравнениями, у которых старший '''[[Задачі: Переставна і сполучна властивості множення. Коефіцієнт|коэффициент]]''' положителен. Поэтому сначала умножим обе части уравнения на -1, получим&nbsp; 9x<sup>2</sup> - 6x + 1 = 0.
+
-
 
+
-
Здесь а = 9, b = -6, с = 1, D = b<sup>2</sup> - 4ас = 36 - 36 = 0. <br>Так как D = 0, то данное квадратное уравнение имеет один корень. Этот корень находится по формуле х = - [[Image:13-06-35.jpg]]. Значит,
+
-
 
+
-
<br>[[Image:13-06-36.jpg|Решение. ]]
+
-
 
+
-
<br>Это уравнение можно было решить по-другому: так как 9х<sup>2</sup> - 6x + 1 = (Зх - IJ, то получаем уравнение (Зх - I)<sup>2</sup> = 0, откуда находим Зх - 1 = 0, т. е. х =[[Image:13-06-37.jpg]] .
+
-
 
+
-
в) Здесь а = 2, b = - 1, с = 3,5, D = b<sup>2</sup> - 4ас = 1 - 4 • 2 • 3,5= 1 - 28 = - 27. Так как D &lt; 0, то данное квадратное уравнение не имеет корней.
+
-
 
+
-
Математики — люди практичные, экономные. Зачем, говорят они, пользоваться таким длинным правилом решения квадратного уравнения, лучше сразу написать общую формулу:
+
-
 
+
-
[[Image:13-06-38.jpg|320px|Формула]]<br><br>Если окажется, что дискриминант D = b<sup>2</sup> - 4ас — отрицательное число, то записанная формула не имеет смысла (под знаком квадратного корня находится отрицательное число), значит, корней нет. Если же окажется, что дискриминант равен нулю, то получаем
+
-
 
+
-
[[Image:13-06-39.jpg|180px|Решение. ]]<br><br>т. е. один корень (говорят также, что квадратное уравнение в этом случае имеет два одинаковых корня:
+
-
 
+
-
[[Image:13-06-40.jpg|Решение. ]]<br> <br>Наконец, если окажется, что b<sup>2</sup> - 4ас &gt; 0, то получаются два корня х<sub>1</sub>и х<sub>2</sub>, которые вычисляются по тем же формулам (3), что указаны выше.
+
-
 
+
-
Само число [[Image:13-06-41.jpg|Число]] в этом случае положительно (как всякий квадратный корень из положительного числа), а двойной знак перед ним означает, что в одном случае (при отыскании х<sub>1</sub> ) это положительное число прибавляется к числу - b, а в другом случае (при отыскании х<sub>2</sub>) это положительное число вы-<br>читается из '''[[Ілюстрації: Лічба предметів. Співвіднесення цифри і числа.|числа]]''' - b.
+
-
 
+
-
У вас есть свобода выбора. Хотите —- решайте квадратное уравнение подробно, используя сформулированное выше правило; хотите — запишите сразу формулу (4) и с ее помощью делайте необходимые выводы.
+
-
 
+
-
'''Пример 5'''. Решить уравнения: <br>[[Image:13-06-42.jpg|420px|Решение. ]]<br><br>'''Решение''',
+
-
 
+
-
а) Конечно, можно использовать формулы (4) или (3), учитывая, что в данном случае [[Image:13-06-43.jpg|180px|Решение. ]] Но зачем выполнять действия с дробями, когда проще и, главное, приятнее иметь дело с целыми числами? Давайте освободимся от знаменателей. Для этого нужно умножить обе части уравнения на 12, т. е. на наименьший общий '''[[Задачі до уроку на тему «Додавання і віднімання дробів з різними знаменниками»|знаменатель]]''' дробей, служащих коэффициентами уравнения. Получим
+
-
 
+
-
[[Image:13-06-44.jpg|240px|Решение. ]]<br>откуда 8х<sup>2</sup> + 10x - 7 = 0.
+
-
 
+
-
А теперь воспользуемся формулой (4)
+
-
 
+
-
[[Image:13-06-45.jpg|480px|Решение. ]]<br><br>б) Мы снова имеем уравнение с дробными коэффициентами: а = 3, b = - 0,2, с = 2,77. Умножим обе части уравнения на 100, тогда получим уравнение с целыми коэффициентами:
+
-
 
+
-
300x<sup>2</sup> - 20x + 277 = 0.
+
-
 
+
-
Далее воспользуемся формулой (4):
+
-
 
+
-
[[Image:13-06-46.jpg|240px|Формула]]<br><br>Простая прикидка показывает, что дискриминант (подкоренное выражение) — '''[[Презентація уроку на тему «Додатні та від'ємні числа. Число 0»|отрицательное число]]'''. Значит, уравнение не имеет корней.
+
-
 
+
-
'''Пример 6.''' Решить уравнение [[Image:13-06-47.jpg|Задание]]<br>Решение. Здесь, в отличие от предыдущего примера, предпочтительнее действовать по правилу, а не по сокращенной формуле (4).
+
-
 
+
-
Имеем а = 5, b = -[[Image:13-06-48.jpg]], с = 1, D = b<sup>2</sup> - 4ас = (- [[Image:13-06-48.jpg]]) <sup>2</sup> - 4 • 5 • 1 = 60 - 20 = 40. Так как D &gt; 0, то квадратное уравнение имеет два корня, которые будем искать по формулам (3)
+
-
 
+
-
[[Image:13-06-49.jpg|320px|Задание]]
+
-
 
+
-
<br>'''Пример 7.''' Решить уравнение <br>х<sup>2</sup> - (2р + 1)x +(р<sup>2</sup>+р-2) = 0
+
-
 
+
-
Решение. Это квадратное уравнение отличается от всех рассмотренных до сих пор квадратных уравнений тем, что в роли коэффициентов выступают не конкретные числа, а буквенные выражения. Такие уравнения называют уравнениями с буквенными коэффициентами или уравнениями с параметрами. В данном случае параметр (буква) р входит в состав второго коэффициента и свободного члена уравнения.
+
-
 
+
-
Найдем дискриминант:
+
-
 
+
-
[[Image:13-06-50.jpg|480px|Задание]]<br><br>'''Пример 8'''. Решить '''[[Линейное уравнение с двумя переменными и его график|уравнение]]''' рx<sup>2</sup> + (1 - р) х - 1 = 0. <br>Решение. Это также уравнение с параметром р, но, в отличие от предыдущего примера, его нельзя сразу решать по формулам (4) или (3). Дело в том, что указанные формулы применимы к квадратным уравнениям, а про заданное уравнение мы этого пока сказать не можем. В самом деле, а вдруг р = 0? Тогда <br>уравнение примет вид 0 • x<sup>2</sup>+ (1-0)x- 1 = 0, т. е. х - 1 = 0, откуда получаем х = 1. Вот если точно известно, что [[Image:13-06-51.jpg]], то можно применять формулы корней квадратного уравнения:
+
-
 
+
-
[[Image:13-06-52.jpg|480px|Задание]]
+
-
 
+
-
[[Image:13-06-53.jpg|480px|Задание]]
+
-
 
+
-
<br>''Мордкович А. Г., [http://xvatit.com/vuzi/ '''Алгебра.'''] 8 кл.: Учеб. для общеобразоват. учреждений.— 3-е изд., доработ. — М.: Мнемозина, 2001. — 223 с: ил. ''<br>  
+
 +
<br>
 +
[[Image:8kl_kv.yravnenie06.jpg|500x500px|квадратные уравнения]]
<br>  
<br>  
-
<sub>Учебники и книги по всему предметам, домашняя работа, [[Гипермаркет знаний - первый в мире!|онлайн]] библиотеки книжек, планы конспектов уроков по математике, рефераты и конспекты уроков по математике для 8 класса [[Математика|скачать]]</sub>
+
И если древний человек уже тогда применял для решения жизненных вопросов квадратные уравнения, то через столько лет изучения этого вопроса, их значение нисколько не уменьшилось, а даже наоборот увеличилось. Давайте с вами поразмыслим, где же теперь нашли применение квадратные уравнения, если не брать во внимание их изучение в школах и различных ВУЗах.
-
<br>
+
Изучая тему квадратных уравнений, мы как-то не задумывались о том, что квадратные уравнения имеют широкое практическое применение.
-
'''<u>Содержание урока</u>'''
+
Без квадратных уравнений не обойтись при различных расчетах. Их можно использовать при строительстве, чтобы выяснить траекторию движения планет, в самолетостроении. Важны арифметические расчеты и в спорте.  
-
<u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока                      '''
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас 
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии
+
-
+
-
'''<u>Практика</u>'''
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников
+
-
+
-
'''<u>Иллюстрации</u>'''
+
-
<u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа '''
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты
+
-
+
-
'''<u>Дополнения</u>'''
+
-
<u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты'''
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов                         
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие
+
-
'''<u></u>'''
+
-
<u>Совершенствование учебников и уроков
+
-
</u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике'''
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми
+
-
+
-
'''<u>Только для учителей</u>'''
+
-
<u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки '''
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год 
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации 
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения
+
-
+
-
+
-
'''<u>Интегрированные уроки</u>'''<u>
+
-
</u>
+
-
 
+
-
<br>
+
-
Если у вас есть исправления или предложения к данному уроку, [http://xvatit.com/index.php?do=feedback напишите нам].
+
'''Домашнее задание:'''
-
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - [http://xvatit.com/forum/ Образовательный форум].
+
<br>
 +
[[Image:8kl_kv.yravnenie07.jpg|500x500px|квадратные уравнения]]
 +
<br>

Версия 10:42, 19 июня 2015

Полужирное начертание

Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика:Формулы корней квадратных уравнений

Квадратные уравнения

Содержание

Определение квадратного уравнения

Из курса математики предыдущих классов вам уже известно, что такое уравнение, а вот какие уравнения называются квадратными, нам еще предстоит разобраться. Если вы слышите такое словосочетание, как «квадратное уравнение», то ключевым словом в этой терминологии является слово «квадратное».

Ну а теперь давайте более подробно рассмотрим, как должно выглядеть квадратное уравнение. А раз оно «квадратное», то это говорит о том, что в таком уравнении обязательно должен присутствовать икс в квадрате, также может быть икс в первой степени и простое число. Если говорить более простым языком, то в таком уравнении должен присутствовать икс, но его степень не должна быть больше двойки.

Но, а если говорить языком математики, то это такое уравнение, которое имеет вид:

ax2 + bx + c = 0,

где a, b, c — некоторые числа (a ≠ 0), x — неизвестное.

Числа, которые присутствуют в квадратном уравнении, называются коэффициентами этого квадратного уравнения:

• a – является первым коэффициентом квадратного уравнения;
• b – выступает в роли второго коэффициента;
• c - называют его свободным членом.

В общем, ясли рассматривать квадратное уравнение, которое имеет вид:

ax2 + bx + c = 0

То мы с вами видим, что в этом квадратном уравнении с его левой стороны есть полный набор членов, где есть икс в квадрате с коэффициентом a, также икс в первой степени с коэффициентом b, ну и свободный член c.

Квадратные уравнения, в котором присутствуют все три слагаемых, называются полными.

Они имеют такой вид:


квадратные уравнения

Но если, к примеру, взять коэффициент b, который равен 0, то получается, что у нас отсутствует икс в первой степени. Или же c равняется нулю, то тогда наше уравнение остается без свободного члена.

Из выше сказанного делаем вывод, что перед нами квадратное уравнение, у которого отсутствует коэффициент или свободный член. Такие квадратные уравнения, у которых чего-то не хватает, называются неполными квадратными уравнениями.

Таким образом, уравнения, у которых один из коэффициентов b или c равны нулю, являются неполными квадратными уравнениями и имеют вид, например:


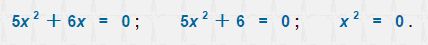
квадратные уравнения

Если же в квадратном уравнении старший коэффициент равняется единице, то такое уравнение носит название приведенного квадратного уравнения.


квадратные уравнения

Способы решения квадратных уравнений


квадратные уравнения

Зачем уметь решать квадратные уравнения


квадратные уравнения

На протяжении изучения всего курса алгебры в школе, изучению уравнений отводится больше часов, чем на какие-либо другие темы по математике. А задумывались ли вы, почему так? Дело в том, что умение решать уравнения имеют не только огромное значение для досконального знания математики и естественных законов, но эти знания пригодятся вам и в практических целях.

Дело в том, что в повседневном реальном мире придется сталкиваться с различными проблемами, где никак не обойтись без решения различных видов уравнений. Научившись их решать и овладев их способами решения, в дальнейшем вы сможете легко найти ответы в любой области науки и техники.

А умение понимать и решать квадратные уравнения, является фундаментом к освоению знаний математических наук.

История возникновения и развития квадратных уравнений

Необходимость в умении решать уравнения возникла еще в глубокой древности, при этом уже тогда люди решали уравнения не только первой степени, но и второй. Это было продиктовано потребностью человека научиться вычислять площади земельных участков, а также делать шаги в развитии таких наук, как астрономия, физика, математика и т.д.

Первыми умельцами в решении квадратных уравнений можно назвать жителей Вавилона. Они их научились решать еще 4000 лет до нашей эры. Естественно, что правила решения квадратных уравнений в вавилонских текстах далеко отличались от современных, но по существу они близки. В вавилонских трактатах не было понятия отрицательного числа, да и общие методы их решения кардинально отличались.

Также пользовался решением квадратных уравнений и древнеиндийский математик Баудхаяма.

В Европе первые формулы решения этих уравнений появились лишь в 1202 г. . Они были описаны итальянским математиком Леонардом Фибоначчи в его знаменитой книге «Книге абака».

Немного позднее изучением этого важного математического вопроса с квадратными уравнениями занялись и такие ученые, как Ньютон, Франсуа Виет, Рене Декарт и другие выдающиеся математики.

Применение квадратных уравнений в современной жизни


квадратные уравнения

И если древний человек уже тогда применял для решения жизненных вопросов квадратные уравнения, то через столько лет изучения этого вопроса, их значение нисколько не уменьшилось, а даже наоборот увеличилось. Давайте с вами поразмыслим, где же теперь нашли применение квадратные уравнения, если не брать во внимание их изучение в школах и различных ВУЗах.

Изучая тему квадратных уравнений, мы как-то не задумывались о том, что квадратные уравнения имеют широкое практическое применение.

Без квадратных уравнений не обойтись при различных расчетах. Их можно использовать при строительстве, чтобы выяснить траекторию движения планет, в самолетостроении. Важны арифметические расчеты и в спорте.

Домашнее задание:


квадратные уравнения

Источник — «http://edufuture.biz/index.php?title=%D0%A4%D0%BE%D1%80%D0%BC%D1%83%D0%BB%D1%8B_%D0%BA%D0%BE%D1%80%D0%BD%D0%B5%D0%B9_%D0%BA%D0%B2%D0%B0%D0%B4%D1%80%D0%B0%D1%82%D0%BD%D1%8B%D1%85_%D1%83%D1%80%D0%B0%D0%B2%D0%BD%D0%B5%D0%BD%D0%B8%D0%B9»

Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки

©  Автор системы образования 7W и Гипермаркета Знаний - Владимир Спиваковский

При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов - гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.

Разработка - Гипермаркет знаний 2008-

Ждем Ваши замечания и предложения на email:
По вопросам рекламы и спонсорства пишите на email: