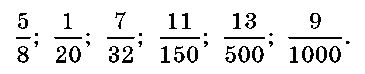Текущая версия на 12:28, 26 июня 2015

Гіпермаркет Знань>>Математика>>Математика 5 клас>>Дробові числа. Звичайні дроби.

Дробові числа. Звичайні дроби. Правильні та неправильні дроби

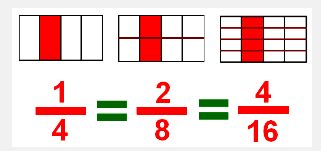
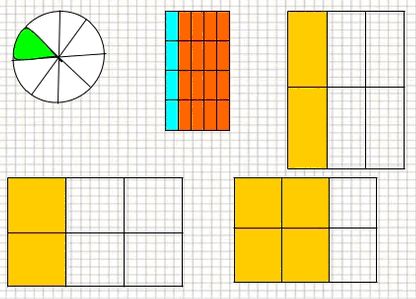
Дробові числа

Дробові числа використовуються тоді, коли потрібно позначити не цілу величину, а якусь її частину. Давайте для кращого розуміння дробових чисел розглянемо на прикладі даного запису цих чисел:

Отже перед нами дробове число, де два поділено на чотири. Що це означає? На цьому малюнку ми бачимо, що 2 – виступає чисельником цього дробу, а 4 – є його знаменником. При записі дробових чисел замість значка поділу прийнято ставити горизонтальну риску дробу. У дробових числах завжди чисельник пишуть зверху над рискою дробу, а знаменник знизу під цією рискою.

Звичайні дроби

Дроби, де чисельник і знаменник мають натуральні числа, носять назву звичайних дробів. Про що ж нам розповідає запис звичайного дробу? Звичайні дроби мають знаменник, який нам дає знати на скільки рівних частин поділена ціла величина. А от чисельник повідомляє скільки частин взято від цілої величини.

Подивіться уважно на малюнок. В першому випадку ми бачимо, що ціла частина величини поділена на чотири частини, з яких взята одна частина. В другому випадку ціла частина величини поділена на вісім частин, з яких взято дві.

Отже, робимо висновок, що звичайні дроби являються часткою двох натуральних чисел. В звичайному дробі чисельник виконує роль діленого, а знаменник є його дільником.

Але, крім того звичайні дроби можуть бути правильними і неправильними. До правильних дробів належать такі звичайні дроби, в яких чисельник менший від знаменника. А от якщо у звичайних дробах чисельник більший, ніж знаменник, то такі звичайні дроби називаються неправильними.

Якщо ми подивимось на малюнок, де зображені правильні дроби, то побачимо, що вони завжди більші за одиницю.

А от в неправильних звичайних дробах чисельник зі знаменником можуть мати однакові числа, тоді такі звичайні дріби дорівнюють одиниці. А в дробах, де чисельник більший за знаменник, такі звичайні дроби завжди більші за одиницю.

Історія появи математичного дробу

Мабуть кожному з вас буде цікаво дізнатися про те, як і коли виникли дроби? І якщо з натуральними числа більш менш відомо, що вони виникли в результаті того, що людині потрібно було рахувати предмети, лічити кількість тварин та вимірювати довжини площі, об’єми.

Але не в усіх випадках в результаті вимірювань виходили натуральні числа, а найчастіше діставалися якісь частини величини.

Бо коли первісна людина з полювання приносила здобич у свою печеру, то їй потрібно було її розділити, а без дробового поділу це зробити було неможливо. Вполювавши двох буйволів, потрібно було цю здобич поділити на чотирьох мисливців. Отак, завдяки потребі в неповних величинах і виникло поняття дробу. Тому історія виникнення дробів ведеться майже з самого початку розвитку людства.

Історичні знахідки свідчать про те, що єгиптяни уміли оперувати дробами більш ніж чотири тисячі років тому. Зрозуміло що в ті часи у людини не було потрібних математичних знань та й загальноприйнятого позначення дробів людина в той час ще не знала, тому у кожній країні використовували свої позначки дробів. Єгиптяни в ті далекі часи застосовували одиничні дроби, які зображали, ставлячи крапку над знаменником.

Трохи пізніше, приблизно понад 2500 років тому, в своїх обчислення почали використовувати дроби і греки. В той час вони вже вміли користуватися як одиничними дробами, так дробами, які мали загальний вигляд.

Люди в Київській Русі дробам дали назву часток, а потім їх стали називати ламаними числами. А ось подивіться які назви мали найпоширеніші дроби на Русі:

Домашнє завдання

Завдання 1. Які дроби ви бачите? Назвіть їх. Перечисліть всі чисельники зображених дробів. Назвіть їх займенники. Дайте пояснення, що означають ці дроби.

Завдання 2. Запишіть яка частина зафарбована та прочитайте дроби.

Завдання 3. Намалюйте коло. Розділіть його на вісім рівних частин. Зафарбуйте олівцем три частини. Назвіть дріб, який ви отримали.

 конспект уроку і опорний каркас 
 задачі та вправи,самоперевірка 
 ілюстрації: відеокліпи, аудіо, фотографії, графіки, таблиці, комікси, мультимедіа
 реферати
 фішки для допитливих