KNOWLEDGE HYPERMARKET

Координатная плоскость (6 класс)
 
(4 промежуточные версии не показаны)
Строка 3: Строка 3:
'''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 6 класс|Математика 6 класс]]>>Математика: Координатная плоскость'''  
'''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 6 класс|Математика 6 класс]]>>Математика: Координатная плоскость'''  
-
<br> '''Координатная плоскость'''
 
-
<br> Места в зрительном зале кинотеатра задают двумя '''[[Ілюстрації: Лічба предметів. Співвіднесення цифри і числа.|числа]]''': первым числом обозначают номер ряда, а вторым — номер кресла в этом ряду (см. рис. на форзаце). При этом места (3; 8) и (8; 3) различны: первое является креслом № 8 в третьем ряду, а второе — креслом № 3 в восьмом ряду.
+
<h2>Что такое координатная плоскость?</h2>
-
Подобным образом можно обозначить и положение точки на плоскости. Для этой цели на плоскости проводят две перпендикулярные координатные прямые х и у, которые пересекаются в начале отсчета — точке О (рис. 113). Эти прямые называют системой координат на плоскости, а точку О — началом координат. Плоскость, на которой выбрана система координат, называют координатной '''[[Плоскость. Прямая. Луч|плоскостью]]'''.  
+
Термин «координаты» в переводе с латинского языка значит слово «упорядоченный».
-
Пусть М — некоторая точка плоскости. Проведем через нее прямую МА, перпендикулярную координатной прямой х, и прямую MB, перпендикулярную координатной прямой у. Так как точка А имеет координату 6, а точка В — координату -5, то положение точки M определяется парой чисел (6; —5). Эту пару чисел называют координатами точки M. Число 6 называют абсциссой точки M, а число -5 называют ординатой точки M. Координатную прямую х называют осью абсцисс, а координатную прямую у — осью ординат.  
+
Допустим, нам нужно обозначить положение точки на плоскости. Для этого мы берем 2 перпендикулярные прямые, которые называются осями координат, где Х будет осью абсцисс, У- осью ординат, а началом координат будет точка О. Образованные с помощью осей координат прямые углы, будут называться координатными углами.
-
Точку M с абсциссой 6 и ординатой -5 обозначают так: M (6; —5). При этом всегда на первом месте пишут абсциссу точки, а на втором — ее ординату. Если переставить '''[[Шкалы и координаты|координаты]]'''&nbsp; местами, то получится другая точка N( — 6; 6), которая показана на рисунке 113.  
+
Так мы подошли к определению и теперь знаем, что координатной плоскостью является плоскость с заданной системой координат.
-
<br>&nbsp;&nbsp;[[Image:2010-42.jpg|480px|Координатная плоскость]]<br>&nbsp;<br>''Каждой точке М на координатной плоскости соответствует пара чисел: ее абсцисса и ордината. Наоборот, каждой паре чисел соответствует одна точка плоскости, для которой эти числа являются координатами. '' На рисунке 114 показано, как попасть в точку С с координатами ( — 4; —3): сначала надо пройти по оси х от начала отсчета влево на 4 единицы, а потом на 3 единицы вниз.
+
А теперь давайте посмотрим, нумерацию координатных углов:
-
В географии положение точек на земной поверхности тоже определяют двумя числами — географическими координатами: широтой и долготой.  
+
<br>
 +
[[Image:6kl_Koord_Plossk01.jpg|300x300px|коорд. плоскость]]
 +
<br>
-
[[Image:2010-09.jpg]]Под каким углом пересекаются координатные прямые х и у, образующие систему координат на плоскости? Как называют каждую из этих прямых? Как называют точку пересечения этих прямых? Как называют пару чисел, определяющих положение точки на плоскости? Как называют первое число? второе число? Расскажите, как найти абсциссу и ординату точки на координатной плоскости. Расскажите, как построить точку по ее координатам.
+
Теперь давайте с вами отобразим прямоугольную систему координат и отметим в ней точку M.
-
 
+
-
1374. По [http://xvatit.com/relax/photoshop-online.php '''рисунку'''] 115 определите, сколько клеток надо пройти слева направо и сколько снизу вверх, чтобы попасть из точки О в точки М, К, Р и N.
+
-
 
+
-
<br>[[Image:2010-43.jpg|480px|Координатная плоскость]]
+
-
 
+
-
1375. Шестиклассники участвовали в спортивной игре. Сначала звено было в точке О (рис. 116). Командир звена получил приказ: «Идите на восток 6 км, а затем на север 4 км».
+
-
 
+
-
Назовите координаты точки В, в которую должно попасть это звено. Сформулируйте приказы для других звеньев, которые должны попасть из точки О в точки С, D, Е, К, Af, N. Назовите координаты этих точек.
+
-
 
+
-
1376.&nbsp;&nbsp; &nbsp;Возьмите географическую карту и назовите широту и долготу городов: Москвы, Киева, Алма-Аты.
+
-
 
+
-
1377.&nbsp;&nbsp; &nbsp;Постройте '''[[Презентація уроку на тему «Координатна пряма. Раціональні числа»|координатные прямые]]''' x и у и отметьте точки А (2; 8), В(3;-4), С (-4; 5), D(-3; -7), Е(0; 5), М(0; -4), K(6; 0), Р(-7;0).
+
-
 
+
-
1378.&nbsp;&nbsp; &nbsp;Найдите координаты точек А, В, С и D (рис. 117).<br>[[Image:2010-44.jpg|320px|Координатная плоскость]]&nbsp;&nbsp; &nbsp;&nbsp;&nbsp;&nbsp; <br>
+
 +
<br>
 +
[[Image:6kl_Koord_Plossk02.jpg|300x300px|коорд. плоскость]]
<br>  
<br>  
-
[[Image:2010-09g.jpg]]&nbsp;Запись M ( — 2; 7) читают так: — точка эм с абсциссой минус два и ординатой семь<br>—&nbsp;&nbsp; &nbsp;точка эм с координатами минус два и семь<br>—&nbsp;&nbsp; &nbsp;координаты точки эм — пара чисел минус два и семь<br>
+
Далее нам нужно прочертить через точку М прямую, которая будет параллельна оси У. Теперь, смотрим, что у нас вышло. Как видим, что прямая пересекает ось Х в той точке, в которой координата будет равна −2. Данная координата является абсциссой точки M.
-
1379.&nbsp;&nbsp; &nbsp;У каких точек на координатной плоскости абсцисса равна нулю? У каких точек равна нулю ордината? Какая точка имеет координаты (0; 0)?
+
Теперь нам нужно прочертить через точку М прямую, которая будет параллельна оси Х.
-
1380.&nbsp;&nbsp; &nbsp;Где расположены на координатной плоскости точки, абсцисса которых равна 4? А где расположены точки, ордината которых равна —1?
+
Мы с вами видим, что эта прямая пересекает ось Х в той точке, координата которой равняется трем. Вот эта координата будет ординатой точки М.
-
1381.&nbsp;&nbsp; &nbsp;Изобразите на координатной плоскости точки А (-2; —2), Б( — 1; -1), С(0; 0), D(1; 1), Е(2; 2). Проверьте с помощью линейки, лежат ли эти точки на одной прямой и лежит ли на этой прямой точка M ( — 5; 5).
+
Запись координат токи М будет выглядеть так:
-
1382. Постройте на координатной плоскости '''[[Склад числа 4.Чотирикутник. Розпізнавання геометричних фігур. Задачі та вправи|четырехугольник]]''' ABCD, если А(—10;— 2), В( —2; —2), С(—2; —6), D (—10; —6). Является ли он прямоугольником? квадратом? Найдите периметр и площадь этого четырехугольника, если единичный отрезок равен 1 см. Проведите отрезки АС и BD и найдите координаты точки Е пересечения этих отрезков.
+
'''M(x;y)'''
-
1383.&nbsp;&nbsp; &nbsp;Постройте треугольник ОВС, где О (0; 0), В (4; 6), С(1;5).  
+
В такой записи всегда на первое место ставят абсциссу, а на второе – ординату. Если рассмотреть на примере координат точки М(-2;3), то -2 выступает в роли абсциссы точки М, а ординатой этой точки будет число 3.
-
1384.&nbsp;&nbsp; &nbsp;На миллиметровой бумаге (рис. 118) отмечены точки А, В, С, D, Е, F, К и М. Найдите их координаты.  
+
Из этого следует, что на координатной плоскости каждой точке М соответствует такая пара чисел, как ее абсцисса и ордината. Верным будет и утверждение наоборот, то есть, каждой такой паре чисел соответствует одна точка плоскости, для которой эти числа являются координатами.
-
1385.&nbsp;&nbsp; &nbsp;В координатной '''[[Плоскость. Прямая. Луч|плоскости]]''' проведена линия (рис. 119). Найдите на этой линии точку:
+
'''Задание:'''
-
а)&nbsp;&nbsp; &nbsp;абсцисса которой равна 2; 1,7; —1,2;
+
<br>
 +
[[Image:6kl_Koord_Plossk03.jpg|500x500px|коорд. плоскость]]
 +
<br>
-
б)&nbsp;&nbsp; &nbsp;ордината которой равна 1,8; 2,1; —1,6; —2,5; —3,2.
+
<h2>Координатная плоскость в жизни</h2>
-
1386.&nbsp;&nbsp; &nbsp;Даны точки А (1; 3), В (-1; 4), С (7; -5), D (0; 6). Какие из этих точек расположены: а) выше оси абсцисс; б) левее оси ординат?<br>[[Image:2010-45.jpg|480px|Координатная плоскость]]<br><br>1387. Вычислите устно:
+
Как по вашему, может ли пригодиться в повседневной жизни знания о координатной плоскости? И доводилось ли вам слышать такую фразу, как «оставьте свои координаты» или «по каким координатам вас можно найти»? И задумывались ли вы над тем, что может обозначать эти выражения?  
-
<br>[[Image:2010-46.jpg|480px|Задание]]<br>1388.&nbsp;&nbsp; &nbsp;Что больше: x или x<sup>2</sup>? х<sup>2</sup> или x<sup>3</sup>?
+
Оказывается все очень просто и банально и это значит местонахождение того или иного объекта, по которому легко найти человека или какое-то определенное место. Можно уверенно утверждать, что системы координат необходимы в практической жизни человека повсеместно.  
-
1389.&nbsp;&nbsp; &nbsp;Найдите все '''[[Фішки для допитливих до уроку: Дробові числа. Звичайні дроби.|дроби]]''' со знаменателем 15, которые больше и меньше [[Image:2010-47.jpg]].<br>[[Image:2010-09m.jpg]]1390. Числа 90 и 100 разделили на одно и то же число, ilii в первом случае получили остаток 18, а во втором случае — остаток 4. Найдите делитель.<br>1391. Из корзины взяли 6 яблок, затем треть остатка и еще 6 яблок. После этого в корзине осталась половина первоначального числа яблок. Сколько яблок было в корзине?
+
Такой системой координат может быть как домашний адрес, так и номер телефона, место работы и т.д.
-
[[Image:2010-09m.jpg]]1392. Попробуйте найти простой способ для вычисления значения выражения<br>[[Image:2010-48.jpg|480px|Задание]]<br>1393.&nbsp;&nbsp; &nbsp;Начертите какой-нибудь треугольник ABC. Через вершину С проведите прямую ''I'', параллельную стороне АВ, и прямую ''m'', перпендикулярную стороне АВ.<br>1394.&nbsp;&nbsp; &nbsp;Найдите длину окружности, радиус которой 7 см, 0,7 см, 0,14 см, приняв [[Image:2010-49.jpg]]<br>1395.&nbsp;&nbsp; &nbsp;Найдите радиус окружности, длина которой 6,28 мм, 3,14 см, 0,0628 м, приняв [[Image:2010-50.jpg]].<br>1396.&nbsp;&nbsp; &nbsp;Вычислите:<br>[[Image:2010-51.jpg|420px|Задание]]<br>1397.&nbsp;&nbsp; &nbsp;Найдите объем и '''[[Урок 19. Площадь фигур|площадь]]''' поверхности куба, ребро которого равно: а) 4 см; б) 0,2 м.  
+
Ведь даже при покупке билетов на поезд, вы знаете не только его номер и место назначения, но и обязательно должен быть указан номер вагона и места.  
-
1398.&nbsp;&nbsp; &nbsp;Решите уравнение:
+
Чтобы пойти в гости к однокласснику, недостаточно знать только дом, в котором он живет, а нужно еще и знать номер квартиры.
-
1) 0,8 • (9 + 2х) = 0,5 • (2 - 3x);
+
'''Задание'''
-
2) 0,5 • (x + 3) = 0,8 • (10 - х).  
+
1. Какими сведениями вы должны владеть, чтобы занять место в театре?<br>
 +
2. Какие данные нужно иметь, чтобы определить точки на земной поверхности?<br>
 +
3. По каким координатам можно определить место в кинотеатре?<br>
 +
4. Что необходимо знать, чтобы определелить положения фигуры на шахматной доске?<br>
 +
5. Какими координатами вы пользуетесь при игре в морской бой?<br>
-
1399.&nbsp;&nbsp; &nbsp;Решите задачу:
+
<h2>Историческая справка</h2>
-
1) На заводе производится смена оборудования. После того как 51 станок заменили новыми, осталось заменить еще 83% станков. Сколько всего станков на заводе надо заменить новыми?
+
Идея использования координат появилась еще в глубокой древности. Первоначально их применять начали астрономы, для определения небесных светил и географы – для определения местонахождения и объектов на поверхности Земли.
-
2) Купили пачку бумаги. После того как израсходовали 30 листов, осталось 85% пачки. Сколько листов бумаги было в пачке?<br>
+
Благодаря трудам древнегреческого астронома Клавдия Плотомея уже во втором веке ученые научились определять долготу и широту.  
-
1400. Решите уравнение:<br>1)&nbsp;&nbsp; &nbsp;(13,4 — у) •4,3 — 20,05 = 78,05 + 6,7 • y;<br>2)&nbsp;&nbsp; &nbsp;(16,2— х) • 3,2 — 50,08 = - 8,12 — 5,1 • x.
+
А известно ли вам, почему в математике существует такое понятие, как «Декартова система координат»? Оказывается метод координат, который имеет общематематическое значение, был открыт французскими математиками Пьером Ферма и Рене Декартом в XVII в., а в 1637 году Рене Декарт впервые описал его в книге по геометрии.
-
 
+
-
[[Image:2010-09d.jpg]]1401. Постройте ломаные линии ABCDE и MNK по координатам точек А ( — 6; 2), В ( — 4; 6), С (1; 1),D (2; —5), Е (8; -1) и М (-5; -5), N(-1; 7), К( 8; 4). Найдите координаты точек пересечения '''[[Урок 6. Длина ломаной. Периметр|ломаных]]''' ABCDE и MNK.
+
-
 
+
-
1402.&nbsp;&nbsp; &nbsp;Постройте четырехугольник ABCDE по координатам его вершин А (—8; 6), В (6; 5), С (1; —3), D(—7; 1). Найдите координаты точки пересечения отрезков АС и BD.<br>
+
-
 
+
-
1403.&nbsp;&nbsp; &nbsp;Отметьте на координатной плоскости точки М (0; 5), N (8; 1), С (2; 2), D ( —6; —2). Найдите координаты точки пересечения прямых MN и CD. На какой из этих прямых лежит точка К (0; 1)?<br>
+
-
 
+
-
1404.&nbsp;&nbsp; &nbsp;Постройте треугольник АВК по координатам его вершин А ( — 2; —2), В( 1; 5), К (6; —2). Найдите координаты точки пересечения стороны АК с осью ординат.<br>
+
-
 
+
-
1405.&nbsp;&nbsp; &nbsp;Решите '''[[Рівняння з двома змінними та його розв'язок. Презентація уроку|уравнение]]''':
+
-
 
+
-
а)&nbsp;&nbsp; &nbsp;-3,7•(2,5x-7,6) =-3,66 + 2,1x;<br>б)&nbsp;&nbsp; &nbsp;0,4 • (у—0,6)=0,5 • (у—0,8)+0,08.<br>
+
-
 
+
-
1406.&nbsp;&nbsp; &nbsp;Отметьте точку М и проведите через нее две прямые ''m'' и ''l'' так, чтобы они образовали угол, равный 62°.<br>
+
-
 
+
-
1407.&nbsp;&nbsp;&nbsp; Постройте угол COD, равный 50°. Через точку M, лежащую на стороне OD, проведите прямую m, параллельную стороне ОС, а через точку К, лежащую на стороне ОС, проведите прямую n, параллельную стороне OD. Измерьте '''[[Кут. Вимірювання і побудова кутів. Транспортир. Види кугів. Бісектриса кута. Практикум|транспортиром]]''' углы, образовавшиеся при пересечении прямых mn.<br>
+
-
 
+
-
1408.&nbsp;&nbsp; &nbsp;Найдите значение выражения:
+
-
 
+
-
а)&nbsp;&nbsp;&nbsp; -3,8 • (4 — 4,9) +13,4 • (3 — 2,8);<br>б)&nbsp;&nbsp; &nbsp;-3,636:0,6+ 2,6 • (5-1,1).<br>
+
-
 
+
-
<br> ''Н.Я.Виленкин, А.С. Чесноков, С.И. Шварцбурд, В.И.Жохов, Математика для 6 класса, Учебник для средней школы'' <br>
+
-
 
+
-
<br>
+
-
 
+
-
<sub>Календарно-тематическое планирование по математике, видео по математике [[Гипермаркет знаний - первый в мире!|онлайн]], Математика в школе [[Математика|скачать]]</sub><br>
+
-
 
+
-
<br>
+
-
 
+
-
'''<u>Содержание урока</u>'''
+
-
<u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока'''
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас 
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии
+
-
+
-
'''<u>Практика</u>'''
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников
+
-
+
-
'''<u>Иллюстрации</u>'''
+
-
<u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа '''
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты
+
-
+
-
'''<u>Дополнения</u>'''
+
-
<u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты'''
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов                         
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие
+
-
'''<u></u>'''
+
-
<u>Совершенствование учебников и уроков
+
-
</u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике'''
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми
+
-
+
-
'''<u>Только для учителей</u>'''
+
-
<u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки '''
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год 
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации 
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения
+
-
+
-
+
-
'''<u>Интегрированные уроки</u>'''<u>
+
-
</u>
+
-
 
+
-
<br>
+
-
Если у вас есть исправления или предложения к данному уроку, [http://xvatit.com/index.php?do=feedback напишите нам].  
+
А вот термины «абсцисса», «ордината» и «координаты» были впервые введены Вильгельмом Лейбницем в семнадцатом веке.
-
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - [http://xvatit.com/forum/ Образовательный форум].
+
<h2>Домашнее задание:</h2>
 +
<br>
 +
[[Image:6kl_Koord_Plossk04.jpg|500x500px|коорд. плоскость]]
 +
<br>
 +
<br>
 +
[[Image:6kl_Koord_Plossk05.jpg|500x500px|коорд. плоскость]]
<br>
<br>

Текущая версия на 11:30, 7 июля 2015

Гипермаркет знаний>>Математика>>Математика 6 класс>>Математика: Координатная плоскость


Содержание

Что такое координатная плоскость?

Термин «координаты» в переводе с латинского языка значит слово «упорядоченный».

Допустим, нам нужно обозначить положение точки на плоскости. Для этого мы берем 2 перпендикулярные прямые, которые называются осями координат, где Х будет осью абсцисс, У- осью ординат, а началом координат будет точка О. Образованные с помощью осей координат прямые углы, будут называться координатными углами.

Так мы подошли к определению и теперь знаем, что координатной плоскостью является плоскость с заданной системой координат.

А теперь давайте посмотрим, нумерацию координатных углов:


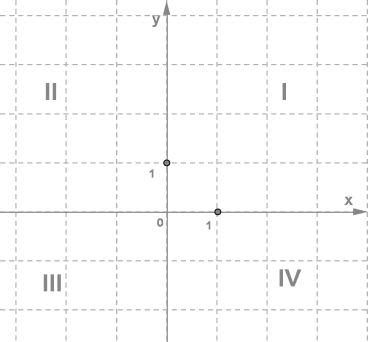
коорд. плоскость

Теперь давайте с вами отобразим прямоугольную систему координат и отметим в ней точку M.


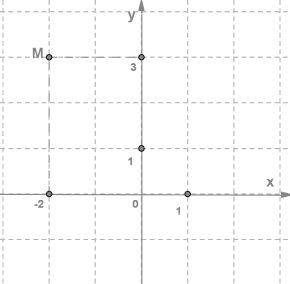
коорд. плоскость

Далее нам нужно прочертить через точку М прямую, которая будет параллельна оси У. Теперь, смотрим, что у нас вышло. Как видим, что прямая пересекает ось Х в той точке, в которой координата будет равна −2. Данная координата является абсциссой точки M.

Теперь нам нужно прочертить через точку М прямую, которая будет параллельна оси Х.

Мы с вами видим, что эта прямая пересекает ось Х в той точке, координата которой равняется трем. Вот эта координата будет ординатой точки М.

Запись координат токи М будет выглядеть так:

M(x;y)

В такой записи всегда на первое место ставят абсциссу, а на второе – ординату. Если рассмотреть на примере координат точки М(-2;3), то -2 выступает в роли абсциссы точки М, а ординатой этой точки будет число 3.

Из этого следует, что на координатной плоскости каждой точке М соответствует такая пара чисел, как ее абсцисса и ордината. Верным будет и утверждение наоборот, то есть, каждой такой паре чисел соответствует одна точка плоскости, для которой эти числа являются координатами.

Задание:


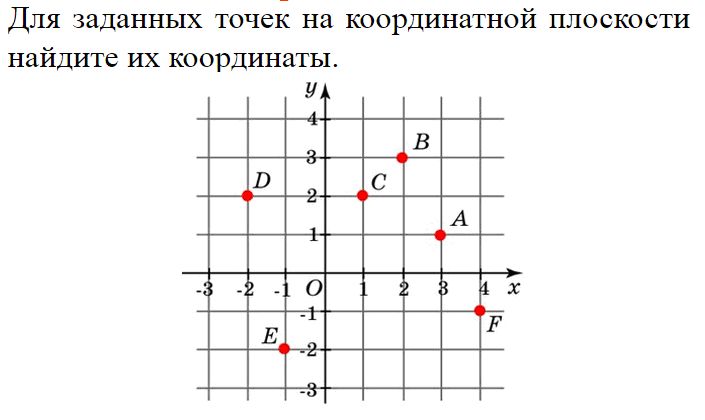
коорд. плоскость

Координатная плоскость в жизни

Как по вашему, может ли пригодиться в повседневной жизни знания о координатной плоскости? И доводилось ли вам слышать такую фразу, как «оставьте свои координаты» или «по каким координатам вас можно найти»? И задумывались ли вы над тем, что может обозначать эти выражения?

Оказывается все очень просто и банально и это значит местонахождение того или иного объекта, по которому легко найти человека или какое-то определенное место. Можно уверенно утверждать, что системы координат необходимы в практической жизни человека повсеместно.

Такой системой координат может быть как домашний адрес, так и номер телефона, место работы и т.д.

Ведь даже при покупке билетов на поезд, вы знаете не только его номер и место назначения, но и обязательно должен быть указан номер вагона и места.

Чтобы пойти в гости к однокласснику, недостаточно знать только дом, в котором он живет, а нужно еще и знать номер квартиры.

Задание

1. Какими сведениями вы должны владеть, чтобы занять место в театре?
2. Какие данные нужно иметь, чтобы определить точки на земной поверхности?
3. По каким координатам можно определить место в кинотеатре?
4. Что необходимо знать, чтобы определелить положения фигуры на шахматной доске?
5. Какими координатами вы пользуетесь при игре в морской бой?

Историческая справка

Идея использования координат появилась еще в глубокой древности. Первоначально их применять начали астрономы, для определения небесных светил и географы – для определения местонахождения и объектов на поверхности Земли.

Благодаря трудам древнегреческого астронома Клавдия Плотомея уже во втором веке ученые научились определять долготу и широту.

А известно ли вам, почему в математике существует такое понятие, как «Декартова система координат»? Оказывается метод координат, который имеет общематематическое значение, был открыт французскими математиками Пьером Ферма и Рене Декартом в XVII в., а в 1637 году Рене Декарт впервые описал его в книге по геометрии.

А вот термины «абсцисса», «ордината» и «координаты» были впервые введены Вильгельмом Лейбницем в семнадцатом веке.

Домашнее задание:


коорд. плоскость

коорд. плоскость

Источник — «http://edufuture.biz/index.php?title=%D0%9A%D0%BE%D0%BE%D1%80%D0%B4%D0%B8%D0%BD%D0%B0%D1%82%D0%BD%D0%B0%D1%8F_%D0%BF%D0%BB%D0%BE%D1%81%D0%BA%D0%BE%D1%81%D1%82%D1%8C_(6_%D0%BA%D0%BB%D0%B0%D1%81%D1%81)»

Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки

©  Автор системы образования 7W и Гипермаркета Знаний - Владимир Спиваковский

При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов - гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.

Разработка - Гипермаркет знаний 2008-

Ждем Ваши замечания и предложения на email:
По вопросам рекламы и спонсорства пишите на email: