|
|
|
| (3 промежуточные версии не показаны) | | Строка 3: |
Строка 3: |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 6 класс|Математика 6 класс]]>>Математика: Координатная плоскость''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 6 класс|Математика 6 класс]]>>Математика: Координатная плоскость''' |
| | | | |
| - | '''Координатная плоскость'''
| |
| | | | |
| | <h2>Что такое координатная плоскость?</h2> | | <h2>Что такое координатная плоскость?</h2> |
| | | | |
| - | Термин «координаты» в переводе с латинского языка обозначает слово «упорядоченный». | + | Термин «координаты» в переводе с латинского языка значит слово «упорядоченный». |
| | | | |
| - | Допустим, нам нужно указать положение точки на плоскости. Для этого мы берем две перпендикулярные прямые, которые называются осями координат, где Х будет осью абсцисс, У- осью ординат, а началом координат будет точка О. Образованные с помощью осей координат прямые углы, будут называться координатными углами. | + | Допустим, нам нужно обозначить положение точки на плоскости. Для этого мы берем 2 перпендикулярные прямые, которые называются осями координат, где Х будет осью абсцисс, У- осью ординат, а началом координат будет точка О. Образованные с помощью осей координат прямые углы, будут называться координатными углами. |
| | | | |
| - | Вот мы с вами и подошли к определению и теперь знаем, что координатной плоскостью называется плоскость, на которой задана система координат.
| + | Так мы подошли к определению и теперь знаем, что координатной плоскостью является плоскость с заданной системой координат. |
| | | | |
| | А теперь давайте посмотрим, нумерацию координатных углов: | | А теперь давайте посмотрим, нумерацию координатных углов: |
| | | | |
| | <br> | | <br> |
| - | [[Image:6kl_Koord_Plossk01.jpg|500x500px|коорд. плоскость]] | + | [[Image:6kl_Koord_Plossk01.jpg|300x300px|коорд. плоскость]] |
| | <br> | | <br> |
| | | | |
| - | Теперь давайте с вами изобразим прямоугольную систему координат, отметив в ней точку M. | + | Теперь давайте с вами отобразим прямоугольную систему координат и отметим в ней точку M. |
| | | | |
| | <br> | | <br> |
| - | [[Image:6kl_Koord_Plossk02.jpg|500x500px|коорд. плоскость]] | + | [[Image:6kl_Koord_Plossk02.jpg|300x300px|коорд. плоскость]] |
| | <br> | | <br> |
| | | | |
| - | Далее нам нужно провести через точку М прямую, которая будет параллельна оси У. Теперь, смотрим, что у нас получилось. Мы видим, что прямая пересекает ось Х в той точке, в которой координата будет равна −2. Это координата является абсциссой точки M. | + | Далее нам нужно прочертить через точку М прямую, которая будет параллельна оси У. Теперь, смотрим, что у нас вышло. Как видим, что прямая пересекает ось Х в той точке, в которой координата будет равна −2. Данная координата является абсциссой точки M. |
| | | | |
| - | Теперь нам нужно провести через точку М прямую, которая будет параллельна оси Х. | + | Теперь нам нужно прочертить через точку М прямую, которая будет параллельна оси Х. |
| | | | |
| | Мы с вами видим, что эта прямая пересекает ось Х в той точке, координата которой равняется трем. Вот эта координата будет ординатой точки М. | | Мы с вами видим, что эта прямая пересекает ось Х в той точке, координата которой равняется трем. Вот эта координата будет ординатой точки М. |
| Строка 37: |
Строка 36: |
| | В такой записи всегда на первое место ставят абсциссу, а на второе – ординату. Если рассмотреть на примере координат точки М(-2;3), то -2 выступает в роли абсциссы точки М, а ординатой этой точки будет число 3. | | В такой записи всегда на первое место ставят абсциссу, а на второе – ординату. Если рассмотреть на примере координат точки М(-2;3), то -2 выступает в роли абсциссы точки М, а ординатой этой точки будет число 3. |
| | | | |
| - | Исходя из этого, можно сделать следующий вывод, что на координатной плоскости каждой точке М соответствует такая пара чисел, как ее абсцисса и ордината. Верным будет и утверждение наоборот, то есть, каждой такой паре чисел соответствует одна точка плоскости, для которой эти числа являются координатами.
| + | Из этого следует, что на координатной плоскости каждой точке М соответствует такая пара чисел, как ее абсцисса и ордината. Верным будет и утверждение наоборот, то есть, каждой такой паре чисел соответствует одна точка плоскости, для которой эти числа являются координатами. |
| | | | |
| | '''Задание:''' | | '''Задание:''' |
| Строка 47: |
Строка 46: |
| | <h2>Координатная плоскость в жизни</h2> | | <h2>Координатная плоскость в жизни</h2> |
| | | | |
| - | А как вы думаете, может ли пригодиться в повседневной жизни знания о координатной плоскости? И доводилось ли вам слышать такую фразу, как «оставьте свои координаты» или «по каким координатам вас можно найти»? И задумывались ли вы над тем, что может обозначать эти выражения?
| + | Как по вашему, может ли пригодиться в повседневной жизни знания о координатной плоскости? И доводилось ли вам слышать такую фразу, как «оставьте свои координаты» или «по каким координатам вас можно найти»? И задумывались ли вы над тем, что может обозначать эти выражения? |
| | | | |
| - | Оказывается все очень просто и банально и это значит местонахождение того или иного объекта, по которому легко найти человека или какое-то определенное место. Можно с уверенностью сказать, что системы координат необходимы в практической жизни человека повсеместно. | + | Оказывается все очень просто и банально и это значит местонахождение того или иного объекта, по которому легко найти человека или какое-то определенное место. Можно уверенно утверждать, что системы координат необходимы в практической жизни человека повсеместно. |
| | | | |
| | Такой системой координат может быть как домашний адрес, так и номер телефона, место работы и т.д. | | Такой системой координат может быть как домашний адрес, так и номер телефона, место работы и т.д. |
| Строка 62: |
Строка 61: |
| | 2. Какие данные нужно иметь, чтобы определить точки на земной поверхности?<br> | | 2. Какие данные нужно иметь, чтобы определить точки на земной поверхности?<br> |
| | 3. По каким координатам можно определить место в кинотеатре?<br> | | 3. По каким координатам можно определить место в кинотеатре?<br> |
| - | 4. Что нужно знать для определения положения фигуры на шахматной доске?<br> | + | 4. Что необходимо знать, чтобы определелить положения фигуры на шахматной доске?<br> |
| | 5. Какими координатами вы пользуетесь при игре в морской бой?<br> | | 5. Какими координатами вы пользуетесь при игре в морской бой?<br> |
| | | | |
Текущая версия на 11:30, 7 июля 2015
Гипермаркет знаний>>Математика>>Математика 6 класс>>Математика: Координатная плоскость
Что такое координатная плоскость?
Термин «координаты» в переводе с латинского языка значит слово «упорядоченный».
Допустим, нам нужно обозначить положение точки на плоскости. Для этого мы берем 2 перпендикулярные прямые, которые называются осями координат, где Х будет осью абсцисс, У- осью ординат, а началом координат будет точка О. Образованные с помощью осей координат прямые углы, будут называться координатными углами.
Так мы подошли к определению и теперь знаем, что координатной плоскостью является плоскость с заданной системой координат.
А теперь давайте посмотрим, нумерацию координатных углов:
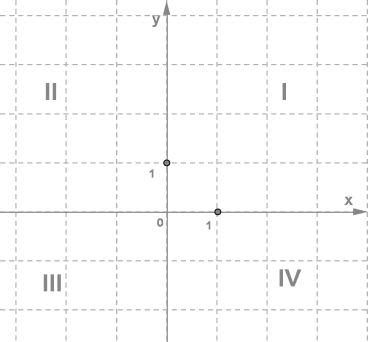
Теперь давайте с вами отобразим прямоугольную систему координат и отметим в ней точку M.
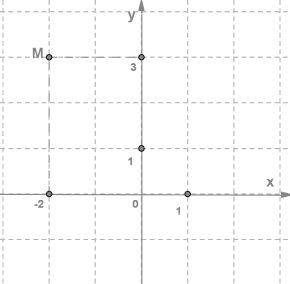
Далее нам нужно прочертить через точку М прямую, которая будет параллельна оси У. Теперь, смотрим, что у нас вышло. Как видим, что прямая пересекает ось Х в той точке, в которой координата будет равна −2. Данная координата является абсциссой точки M.
Теперь нам нужно прочертить через точку М прямую, которая будет параллельна оси Х.
Мы с вами видим, что эта прямая пересекает ось Х в той точке, координата которой равняется трем. Вот эта координата будет ординатой точки М.
Запись координат токи М будет выглядеть так:
M(x;y)
В такой записи всегда на первое место ставят абсциссу, а на второе – ординату. Если рассмотреть на примере координат точки М(-2;3), то -2 выступает в роли абсциссы точки М, а ординатой этой точки будет число 3.
Из этого следует, что на координатной плоскости каждой точке М соответствует такая пара чисел, как ее абсцисса и ордината. Верным будет и утверждение наоборот, то есть, каждой такой паре чисел соответствует одна точка плоскости, для которой эти числа являются координатами.
Задание:
Координатная плоскость в жизни
Как по вашему, может ли пригодиться в повседневной жизни знания о координатной плоскости? И доводилось ли вам слышать такую фразу, как «оставьте свои координаты» или «по каким координатам вас можно найти»? И задумывались ли вы над тем, что может обозначать эти выражения?
Оказывается все очень просто и банально и это значит местонахождение того или иного объекта, по которому легко найти человека или какое-то определенное место. Можно уверенно утверждать, что системы координат необходимы в практической жизни человека повсеместно.
Такой системой координат может быть как домашний адрес, так и номер телефона, место работы и т.д.
Ведь даже при покупке билетов на поезд, вы знаете не только его номер и место назначения, но и обязательно должен быть указан номер вагона и места.
Чтобы пойти в гости к однокласснику, недостаточно знать только дом, в котором он живет, а нужно еще и знать номер квартиры.
Задание
1. Какими сведениями вы должны владеть, чтобы занять место в театре?
2. Какие данные нужно иметь, чтобы определить точки на земной поверхности?
3. По каким координатам можно определить место в кинотеатре?
4. Что необходимо знать, чтобы определелить положения фигуры на шахматной доске?
5. Какими координатами вы пользуетесь при игре в морской бой?
Историческая справка
Идея использования координат появилась еще в глубокой древности. Первоначально их применять начали астрономы, для определения небесных светил и географы – для определения местонахождения и объектов на поверхности Земли.
Благодаря трудам древнегреческого астронома Клавдия Плотомея уже во втором веке ученые научились определять долготу и широту.
А известно ли вам, почему в математике существует такое понятие, как «Декартова система координат»? Оказывается метод координат, который имеет общематематическое значение, был открыт французскими математиками Пьером Ферма и Рене Декартом в XVII в., а в 1637 году Рене Декарт впервые описал его в книге по геометрии.
А вот термины «абсцисса», «ордината» и «координаты» были впервые введены Вильгельмом Лейбницем в семнадцатом веке.
Домашнее задание:


|















