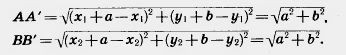|
|
|
| (2 промежуточные версии не показаны) | | Строка 7: |
Строка 7: |
| | '''Параллельный перенос и его свойства''' | | '''Параллельный перенос и его свойства''' |
| | | | |
| - | <br>Наглядно [[Ілюстрації: Поворот. Паралельне перенесення|параллельный перенос]] определяется как преобразование, при котором точки смещаются в одном и том же направлении на одно и то же расстояние (рис. 198). Такое определение не является математически строгим, потому что в нем употребляется выражение «в одном и том же направлении», которое само нуждается в точном определении. В связи с этим параллельному переносу мы дадим другое, отвечающее тому же наглядному представлению, но уже строгое определение. | + | <h2>Общие сведения о параллельном переносе</h2> |
| | + | |
| | + | Наглядно [[Ілюстрації: Поворот. Паралельне перенесення|параллельный перенос]] определяется как преобразование, при котором точки смещаются в одном и том же направлении на одно и то же расстояние (рис. 198). Такое определение не является математически строгим, потому что в нем употребляется выражение «в одном и том же направлении», которое само нуждается в точном определении. В связи с этим параллельному переносу мы дадим другое, отвечающее тому же наглядному представлению, но уже строгое определение. |
| | | | |
| | Введем на плоскости декартовы [[Шкалы и координаты|координаты]] х, у. Преобразование фигуры F, при котором произвольная ее точка (х; у) переходит в точку (х + а; у + b), где а и b одни и те же для всех точек (х; у), называется параллельным переносом (рис. 199). Параллельный перенос задается формулами x' = x + а, у' = у + b. | | Введем на плоскости декартовы [[Шкалы и координаты|координаты]] х, у. Преобразование фигуры F, при котором произвольная ее точка (х; у) переходит в точку (х + а; у + b), где а и b одни и те же для всех точек (х; у), называется параллельным переносом (рис. 199). Параллельный перенос задается формулами x' = x + а, у' = у + b. |
| Строка 13: |
Строка 15: |
| | Эти формулы выражают координаты х', у' точки, в которую переходит [[Точка, пряма, площина. Промінь. Відрізок. Презентація уроку|точка]] (х; у) при параллельном переносе.<br> | | Эти формулы выражают координаты х', у' точки, в которую переходит [[Точка, пряма, площина. Промінь. Відрізок. Презентація уроку|точка]] (х; у) при параллельном переносе.<br> |
| | | | |
| - | [[Image:22-06-146.jpg|480px| Параллельный перенос и его свойства ]] <br>Параллельный перенос есть движение. | + | [[Image:22-06-146.jpg|480px| Параллельный перенос и его свойства ]] <br> |
| | + | |
| | + | <h2>Свойства параллельного переноса</h2> |
| | + | |
| | + | '''Параллельный перенос есть движение.''' |
| | | | |
| | Действительно, две произвольные точки А(х<sub>1</sub>; у<sub>1</sub>) к В (х<sub>2</sub>; у<sub>2</sub>) переходят при параллельном переносе в точки А' (х<sub>1</sub> +а; у<sub>1</sub> + b), В'(х<sub>2</sub> + а; y<sub>2</sub>+b). Поэтому<br>АВ<sup>2</sup>=(х<sub>2</sub>-х<sub>1</sub>)<sup>2</sup>+ (у<sub>2</sub>-у<sub>1</sub> )<sup>2</sup> | | Действительно, две произвольные точки А(х<sub>1</sub>; у<sub>1</sub>) к В (х<sub>2</sub>; у<sub>2</sub>) переходят при параллельном переносе в точки А' (х<sub>1</sub> +а; у<sub>1</sub> + b), В'(х<sub>2</sub> + а; y<sub>2</sub>+b). Поэтому<br>АВ<sup>2</sup>=(х<sub>2</sub>-х<sub>1</sub>)<sup>2</sup>+ (у<sub>2</sub>-у<sub>1</sub> )<sup>2</sup> |
| Строка 21: |
Строка 27: |
| | Отсюда АВ=А'В'. Таким образом, параллельный перенос сохраняет расстояния, а значит, является движением, что и требовалось доказать. | | Отсюда АВ=А'В'. Таким образом, параллельный перенос сохраняет расстояния, а значит, является движением, что и требовалось доказать. |
| | | | |
| - | Название «параллельный перенос» оправдывается тем, что при параллельном переносе точки смещаются по параллельным (или совпадающим) прямым на одно и то же расстояние.<br> | + | '''Название «параллельный перенос» оправдывается тем, что при параллельном переносе точки смещаются по параллельным (или совпадающим) прямым на одно и то же расстояние.'''<br> |
| | | | |
| | [[Image:22-06-147.jpg|480px| Параллельный перенос и его свойства ]] <br>Действительно, пусть точки A (x<sub>1</sub>; y<sub>1</sub>) и В (x<sub>2</sub>; y<sub>2</sub>) переходят в точки A'(x<sub>1</sub>+а; y<sub>1</sub> + b) и В' (х<sub>2</sub> + а; y<sub>2</sub> + b) (рис. 200). Середина отрезка АВ' имеет координаты | | [[Image:22-06-147.jpg|480px| Параллельный перенос и его свойства ]] <br>Действительно, пусть точки A (x<sub>1</sub>; y<sub>1</sub>) и В (x<sub>2</sub>; y<sub>2</sub>) переходят в точки A'(x<sub>1</sub>+а; y<sub>1</sub> + b) и В' (х<sub>2</sub> + а; y<sub>2</sub> + b) (рис. 200). Середина отрезка АВ' имеет координаты |
| Строка 33: |
Строка 39: |
| | [[Image:22-06-149.jpg|320px|Формулы]]<br><br>Таким образом, в этом случае точки АиВ смещаются по прямой АВ на одно и то же расстояние [[Image:22-06-150.jpg]] а прямая АВ переходит в себя. | | [[Image:22-06-149.jpg|320px|Формулы]]<br><br>Таким образом, в этом случае точки АиВ смещаются по прямой АВ на одно и то же расстояние [[Image:22-06-150.jpg]] а прямая АВ переходит в себя. |
| | | | |
| - | <br> ''А. В. Погорелов, [http://xvatit.com/vuzi/ Геометрия] для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> | + | <h2>Повторение темы о параллельном переносе</h2> |
| | | | |
| | + | Мы с вами уже познакомились с такой темой, как параллельный перенос. На этом уроке вы узнали, что такое преобразование на плоскости, где все точки перемещаются на одно и то же расстояние, считается параллельным переносом. |
| | | | |
| | + | Из данного урока, каждому из вас стало понятно, что параллельный перенос является движением, так как при таком переносе любая прямая переходит в такую же параллельную ей прямую. |
| | | | |
| - | <sub>Книги, учебники математике [[Математика|скачать]], конспект на помощь учителю и ученикам, учиться [[Гипермаркет знаний - первый в мире!|онлайн]]</sub> | + | <br> |
| | + | [[Image:8kl_Paraltl01.jpg|400x400px|параллельный перенос]] |
| | + | <br> |
| | + | |
| | + | Если мы посмотрим на рисунок, то можем наглядно представить такое движение, как сдвиг площади в направлении данного вектора на его длину. |
| | | | |
| - | <br> | + | <h2>Свойства, которыми обладает параллельный перенос в пространстве</h2> |
| | | | |
| - | '''<u>Содержание урока</u>'''
| + | • Во-первых, параллельный перенос является движением;<br> |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока '''
| + | • Во-вторых, при выполнении этого действия все точки смещаются по параллельным прямым и притом на одно и то же расстояние;<br> |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас
| + | • В-третьих, при таком переносе прямая имеет свойство переходить в такую же параллельную прямую или в себя саму;<br> |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока
| + | • В-четвертых, независимо от того, какими точками были A и A', но точка A переходит в точку A'. <br> |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы
| + | • В-пятых, при таком переносе, т.е параллельном переносе в пространстве, в любом случае плоскость имеет свойство переходить в себя саму или же такую же параллельную ей плоскость.<br> |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии
| + | |
| | | | |
| - | '''<u>Практика</u>'''
| + | <br> |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения
| + | [[Image:8kl_Paraltl02.jpg|500x500px|параллельный перенос]] |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка
| + | <br> |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников
| + | |
| - |
| + | |
| - | '''<u>Иллюстрации</u>'''
| + | |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа '''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты
| + | |
| - |
| + | |
| - | '''<u>Дополнения</u>'''
| + | |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты'''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие
| + | |
| - | '''<u></u>'''
| + | |
| - | <u>Совершенствование учебников и уроков
| + | |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике'''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми
| + | |
| - |
| + | |
| - | '''<u>Только для учителей</u>'''
| + | |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки '''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения
| + | |
| - |
| + | |
| - |
| + | |
| - | '''<u>Интегрированные уроки</u>'''<u>
| + | |
| - | </u>
| + | |
| | | | |
| | + | <h2>Истрия и применение в науке</h2> |
| | + | |
| | + | Как правило, в каждого понятия есть свой первооткрыватель, но автор параллельного переноса в пространстве, на жаль, нам неизвестен. А вот применение параллельного переноса в пространстве довольно широко. Как правило, такой перенос используют при преобразовании графической функции в математике, в механике, а также в кристаллографии. |
| | + | |
| | + | <br> |
| | + | [[Image:8kl_Paraltl03.jpg|500x500px|параллельный перенос]] |
| | <br> | | <br> |
| | | | |
| - | Если у вас есть исправления или предложения к данному уроку, [http://xvatit.com/index.php?do=feedback напишите нам].
| + | Но если рассматривать трансляция или кристаллографию, то в этом случае перенос приобретает симметричное преобразование, в котором узел пространственной решётки должен совпасть с идентичным ближайшим узлом. В принципе, трансляцию можно отнести к частному случаю параллельного переноса, так как при сдвиге на определенный вектор ее свойства в данной системе не изменяются, а являются вектором трансляции и для нее свойственна трансляционная симметрия. |
| | + | |
| | + | <h2>Примеры из жизни</h2> |
| | + | |
| | + | В повседневной жизни мы с вами также постоянно сталкиваемся с примерами параллельного переноса в пространстве. Таким наглядным примером может быть, применяемая в строительной индустрии скользящая опалубка, этот процесс мы можем наблюдать и при перестановке мебели в квартире, да и следы от подошвы нам также напоминают о параллельном переносе в пространстве. |
| | + | |
| | + | А также, параллельный перенос можно встретить и в таких необычных ситуациях: |
| | + | |
| | + | <br> |
| | + | [[Image:8kl_Paraltl04.jpg|500x500px|параллельный перенос]] |
| | + | <br> |
| | | | |
| - | Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - [http://xvatit.com/forum/ Образовательный форум].
| + | <br> ''А. В. Погорелов, [http://xvatit.com/vuzi/ Геометрия] для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> |
Текущая версия на 07:20, 8 июля 2015
Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика: Параллельный перенос и его свойства
Параллельный перенос и его свойства
Общие сведения о параллельном переносе
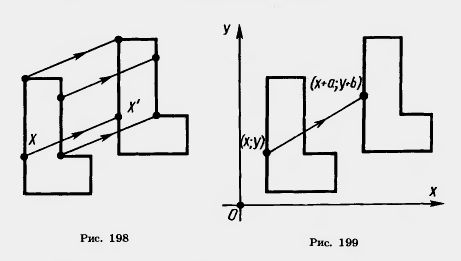
Наглядно параллельный перенос определяется как преобразование, при котором точки смещаются в одном и том же направлении на одно и то же расстояние (рис. 198). Такое определение не является математически строгим, потому что в нем употребляется выражение «в одном и том же направлении», которое само нуждается в точном определении. В связи с этим параллельному переносу мы дадим другое, отвечающее тому же наглядному представлению, но уже строгое определение.
Введем на плоскости декартовы координаты х, у. Преобразование фигуры F, при котором произвольная ее точка (х; у) переходит в точку (х + а; у + b), где а и b одни и те же для всех точек (х; у), называется параллельным переносом (рис. 199). Параллельный перенос задается формулами x' = x + а, у' = у + b.
Эти формулы выражают координаты х', у' точки, в которую переходит точка (х; у) при параллельном переносе.
Свойства параллельного переноса
Параллельный перенос есть движение.
Действительно, две произвольные точки А(х1; у1) к В (х2; у2) переходят при параллельном переносе в точки А' (х1 +а; у1 + b), В'(х2 + а; y2+b). Поэтому
АВ2=(х2-х1)2+ (у2-у1 )2
A'B"2=(х2-х1)2+ (у2-у1 )2
Отсюда АВ=А'В'. Таким образом, параллельный перенос сохраняет расстояния, а значит, является движением, что и требовалось доказать.
Название «параллельный перенос» оправдывается тем, что при параллельном переносе точки смещаются по параллельным (или совпадающим) прямым на одно и то же расстояние.
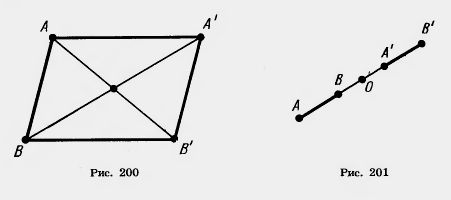
Действительно, пусть точки A (x1; y1) и В (x2; y2) переходят в точки A'(x1+а; y1 + b) и В' (х2 + а; y2 + b) (рис. 200). Середина отрезка АВ' имеет координаты
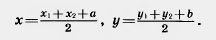
Те же координаты имеет и середина отрезка А'В. Отсюда следует, что диагонали четырехугольника АА'В'В пересекаются и точкой пересечения делятся пополам. Значит, этот четырехугольник — параллелограмм. А у параллелограмма противолежащие стороны А А' и ВВ' параллельны и равны.
Заметим, что у параллелограмма АА'В'В параллельны и две другие противолежащие стороны — АВ и А 'В'. Отсюда следует, что при параллельном, переносе прямая переходит в параллельную прямую (или в себя).
Замечание. В предыдущем доказательстве предполагалось, что точка В не лежит на прямой АА'. В случае, когда точка В лежит на прямой АА', точка В' тоже лежит на этой прямой, так как середина отрезка АВ' совпадает с серединой отрезка ВА' (рис. 201). Значит, все точки А, В, А', В' лежат на одной прямой. Далее,
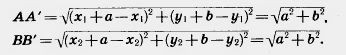
Таким образом, в этом случае точки АиВ смещаются по прямой АВ на одно и то же расстояние 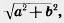 а прямая АВ переходит в себя. а прямая АВ переходит в себя.
Повторение темы о параллельном переносе
Мы с вами уже познакомились с такой темой, как параллельный перенос. На этом уроке вы узнали, что такое преобразование на плоскости, где все точки перемещаются на одно и то же расстояние, считается параллельным переносом.
Из данного урока, каждому из вас стало понятно, что параллельный перенос является движением, так как при таком переносе любая прямая переходит в такую же параллельную ей прямую.
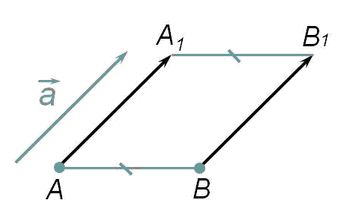
Если мы посмотрим на рисунок, то можем наглядно представить такое движение, как сдвиг площади в направлении данного вектора на его длину.
Свойства, которыми обладает параллельный перенос в пространстве
• Во-первых, параллельный перенос является движением;
• Во-вторых, при выполнении этого действия все точки смещаются по параллельным прямым и притом на одно и то же расстояние;
• В-третьих, при таком переносе прямая имеет свойство переходить в такую же параллельную прямую или в себя саму;
• В-четвертых, независимо от того, какими точками были A и A', но точка A переходит в точку A'.
• В-пятых, при таком переносе, т.е параллельном переносе в пространстве, в любом случае плоскость имеет свойство переходить в себя саму или же такую же параллельную ей плоскость.
Истрия и применение в науке
Как правило, в каждого понятия есть свой первооткрыватель, но автор параллельного переноса в пространстве, на жаль, нам неизвестен. А вот применение параллельного переноса в пространстве довольно широко. Как правило, такой перенос используют при преобразовании графической функции в математике, в механике, а также в кристаллографии.

Но если рассматривать трансляция или кристаллографию, то в этом случае перенос приобретает симметричное преобразование, в котором узел пространственной решётки должен совпасть с идентичным ближайшим узлом. В принципе, трансляцию можно отнести к частному случаю параллельного переноса, так как при сдвиге на определенный вектор ее свойства в данной системе не изменяются, а являются вектором трансляции и для нее свойственна трансляционная симметрия.
Примеры из жизни
В повседневной жизни мы с вами также постоянно сталкиваемся с примерами параллельного переноса в пространстве. Таким наглядным примером может быть, применяемая в строительной индустрии скользящая опалубка, этот процесс мы можем наблюдать и при перестановке мебели в квартире, да и следы от подошвы нам также напоминают о параллельном переносе в пространстве.
А также, параллельный перенос можно встретить и в таких необычных ситуациях:

А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
|