|
|
|
| (1 промежуточная версия не показана) | | Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 11 класс, Геометрия, урок, на Тему, Прямая призма, многоугольники, сечение</metakeywords> | + | '''<metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 11 класс, Геометрия, урок, на Тему, Прямая призма, многоугольники, сечение</metakeywords> |
| | | | |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 11 класс|Математика 11 класс]]>>Математика:Прямая призма''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 11 класс|Математика 11 класс]]>>Математика:Прямая призма''' |
| Строка 6: |
Строка 6: |
| | | | |
| | '''Прямая призма'''<br> | | '''Прямая призма'''<br> |
| | + | |
| | + | <h2>Общие сведения о прямой призме</h2> |
| | | | |
| | <br>'''[[Призма|Призма]]''' называется прямой, если ее боковые ребра перпендикулярны основаниям. В противном случае призма называется наклонной. | | <br>'''[[Призма|Призма]]''' называется прямой, если ее боковые ребра перпендикулярны основаниям. В противном случае призма называется наклонной. |
| Строка 24: |
Строка 26: |
| | | | |
| | <br> | | <br> |
| | + | |
| | + | <h2>Практическое задание</h2> |
| | | | |
| | [[Image:1-07-40.jpg|480px|Прямая призма]]<br> <br>'''''Задача (22)'''''. В наклонной призме проведено '''[[Презентация урока: Изображение призмы и построение ее сечений|сечение]]''', перпендикулярное боковым ребрам и пересекающее все боковые ребра. Найдите боковую поверхность призмы, если периметр сечения равен р, а боковые ребра равны l. | | [[Image:1-07-40.jpg|480px|Прямая призма]]<br> <br>'''''Задача (22)'''''. В наклонной призме проведено '''[[Презентация урока: Изображение призмы и построение ее сечений|сечение]]''', перпендикулярное боковым ребрам и пересекающее все боковые ребра. Найдите боковую поверхность призмы, если периметр сечения равен р, а боковые ребра равны l. |
| | | | |
| - | Решение. Плоскость проведенного сечения разбивает призму на две части (рис. 411). Подвергнем одну из них параллельному переносу, совмещающему основания призмы. При этом получим прямую призму, у которой основанием служит сечение исходной призмы, а боковые ребра равны l. Эта призма имеет ту же боковую поверхность, что и исходная. Таким образом, боковая поверхность исходной призмы равна рl.<br> | + | Решение. Плоскость проведенного сечения разбивает призму на две части (рис. 411). Подвергнем одну из них параллельному переносу, совмещающему основания призмы. При этом получим прямую призму, у которой основанием служит сечение исходной призмы, а боковые ребра равны l. Эта призма имеет ту же боковую поверхность, что и исходная. Таким образом, боковая поверхность исходной призмы равна рl. |
| | | | |
| - | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> | + | <h2>Обобщение пройденной темы</h2> |
| | | | |
| - | <br> <br> <sub>Календарно-тематическое планирование по математике, [http://xvatit.com/it/audio_television/ '''видео'''] по математике [[Гипермаркет знаний - первый в мире!|онлайн]], Математика в школе [[Математика|скачать]]</sub>
| + | А теперь давайте попробуем с вами подвести итоги пройденной темы о призме и |
| | + | вспомним, какими свойствами обладает призма. |
| | | | |
| | + | <br> |
| | + | [[Image:11kl_PramPrizma01.jpg|500x500px|прямая призма]] |
| | <br> | | <br> |
| | | | |
| - | '''<u>Содержание урока</u>'''
| + | '''Свойства призмы''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока '''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии
| + | |
| - |
| + | |
| - | '''<u>Практика</u>'''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников
| + | |
| - |
| + | |
| - | '''<u>Иллюстрации</u>'''
| + | |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа '''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты
| + | |
| - |
| + | |
| - | '''<u>Дополнения</u>'''
| + | |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты'''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие
| + | |
| - | '''<u></u>'''
| + | |
| - | <u>Совершенствование учебников и уроков
| + | |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике'''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми
| + | |
| - |
| + | |
| - | '''<u>Только для учителей</u>'''
| + | |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки '''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения
| + | |
| - |
| + | |
| - |
| + | |
| - | '''<u>Интегрированные уроки</u>'''<u>
| + | |
| - | </u>
| + | |
| | | | |
| | + | • Во-первых, у призмы все ее основания являются равными многоугольниками;<br> |
| | + | • Во-вторых, у призмы все ее боковые грани являются параллелограммами;<br> |
| | + | • В-третьих, у такой многогранной фигуры, как призма, все боковые ребра равны;<br> |
| | + | |
| | + | Также, следует вспомнить, что такие многогранники, как призмы могут быть прямыми и наклонными. |
| | + | |
| | + | '''Какая призма называется прямой?''' |
| | + | |
| | + | Если же у призмы боковое ребро расположено перпендикулярно плоскости ее основания, то такая призма носит название прямой. |
| | + | |
| | + | Не будет лишним напомнить, что боковые грани прямой призмы являются прямоугольниками. |
| | + | |
| | + | '''Какую призму называют наклонной?''' |
| | + | |
| | + | А вот если же у призмы боковое ребро не расположено перпендикулярно плоскости ее основания, то можно смело утверждать, что это наклонная призма. |
| | + | |
| | + | '''Какую призму называют правильной?''' |
| | + | |
| | + | <br> |
| | + | [[Image:11kl_PramPrizma02.jpg|500x500px|прямая призма]] |
| | <br> | | <br> |
| | | | |
| - | Если у вас есть исправления или предложения к данному уроку, [http://xvatit.com/index.php?do=feedback напишите нам]. | + | Если у основания прямой призмы лежит правильный многоугольник, то такая призма является правильной. |
| | + | |
| | + | Теперь вспомним свойства, которыми обладает правильная призма. |
| | + | |
| | + | <h2>Свойства правильной призмы</h2> |
| | + | |
| | + | • Во-первых, всегда основаниями правильной призмы служат правильные многоугольники;<br> |
| | + | • Во-вторых, если рассматривать у правильной призмы боковые грани, то они всегда бывают равными прямоугольниками;<br> |
| | + | • В-третьих, если сравнивать размеры боковых ребер, то в правильной призме они всегда равны.<br> |
| | + | • В-четвертых, правильная призма всегда прямая;<br> |
| | + | • В-пятых, если же в правильной призмы боковые грани имеют форму квадратов, то такую фигуру, как правило, называют полуправильным многоугольником.<br> |
| | + | |
| | + | <h2>Сечение призмы</h2> |
| | + | |
| | + | А теперь давайте рассмотрим сечение призмы: |
| | + | |
| | + | <br> |
| | + | [[Image:11kl_PramPrizma03.jpg|500x500px|прямая призма]] |
| | + | <br> |
| | + | |
| | + | <h2>Домашнее задание</h2> |
| | + | |
| | + | А теперь давайте попробуем закрепить изученную тему с помощью решения задач. |
| | + | |
| | + | Давайте нарисуем наклонную треугольную призму, у которой расстояние между ее ребрами будет равно: 3 см, 4 см и 5 см, а боковая поверхность этой призмы будет равна 60 см2. Имея такие параметры, найдите боковое ребро данной призмы. |
| | + | |
| | + | <h2>Интересно знать</h2> |
| | + | |
| | + | А вы знаете, что геометрические фигуры постоянно окружают нас не только на уроках геометрии, но и в повседневной жизни встречаются предметы, которые напоминают ту или иную геометрическую фигуру. |
| | + | |
| | + | <br> |
| | + | [[Image:11kl_PramPrizma04.jpg|500x500px|прямая призма]] |
| | + | <br> |
| | + | |
| | + | У каждого дома, в школе или на работе имеется компьютер, системный блок которого имеет форму прямой призмы. |
| | + | |
| | + | Если вы возьмете в руки простой карандаш, то вы увидите, что основной частью карандаша, является призма. |
| | + | |
| | + | Идя по центральной улице города, мы видим, что у нас под ногами лежит плитка, которая имеет форму шестиугольной призмы. |
| | | | |
| - | Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - [http://xvatit.com/forum/ Образовательный форум].
| + | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> |
Текущая версия на 18:44, 29 июля 2015
Гипермаркет знаний>>Математика>>Математика 11 класс>>Математика:Прямая призма
Прямая призма
Общие сведения о прямой призме
Призма называется прямой, если ее боковые ребра перпендикулярны основаниям. В противном случае призма называется наклонной.
У прямой призмы боковые грани являются прямоугольниками. При изображении прямой призмы на рисунке боковые ребра обычно проводят вертикально (рис. 410).
Прямая призма называется правильной, если ее основания являются правильными многоугольниками.
Боковой поверхностью призмы (точнее, площадью боковой поверхности) называется сумма площадей боковых граней. Полная поверхность призмы равна сумме боковой поверхности и площадей оснований.
Теорема 19.1. Боковая поверхность прямой призмы равна произведению периметра основания на высоту призмы, т. е. на длину бокового ребра.
Доказательство. Боковые грани прямой призмы — прямоугольники. Основания этих прямоугольников являются сторонами многоугольника, лежащего в основании призмы, а высоты равны длине боковых ребер. Отсюда следует, что боковая поверхность призмы равна
S = a1l + a2l + ... + anl = pl,
где a1,аn — длины ребер основания, р — периметр основания призмы, а I — длина боковых ребер. Теорема доказана.
Практическое задание
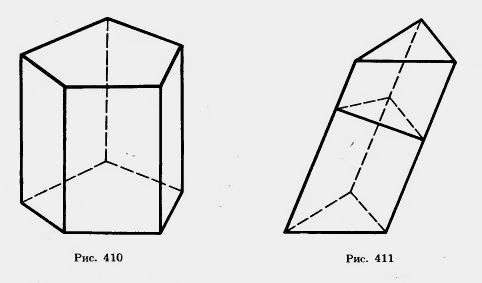
Задача (22). В наклонной призме проведено сечение, перпендикулярное боковым ребрам и пересекающее все боковые ребра. Найдите боковую поверхность призмы, если периметр сечения равен р, а боковые ребра равны l.
Решение. Плоскость проведенного сечения разбивает призму на две части (рис. 411). Подвергнем одну из них параллельному переносу, совмещающему основания призмы. При этом получим прямую призму, у которой основанием служит сечение исходной призмы, а боковые ребра равны l. Эта призма имеет ту же боковую поверхность, что и исходная. Таким образом, боковая поверхность исходной призмы равна рl.
Обобщение пройденной темы
А теперь давайте попробуем с вами подвести итоги пройденной темы о призме и
вспомним, какими свойствами обладает призма.
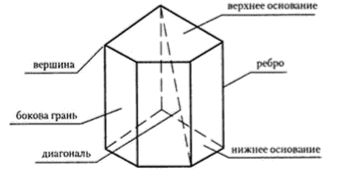
Свойства призмы
• Во-первых, у призмы все ее основания являются равными многоугольниками;
• Во-вторых, у призмы все ее боковые грани являются параллелограммами;
• В-третьих, у такой многогранной фигуры, как призма, все боковые ребра равны;
Также, следует вспомнить, что такие многогранники, как призмы могут быть прямыми и наклонными.
Какая призма называется прямой?
Если же у призмы боковое ребро расположено перпендикулярно плоскости ее основания, то такая призма носит название прямой.
Не будет лишним напомнить, что боковые грани прямой призмы являются прямоугольниками.
Какую призму называют наклонной?
А вот если же у призмы боковое ребро не расположено перпендикулярно плоскости ее основания, то можно смело утверждать, что это наклонная призма.
Какую призму называют правильной?
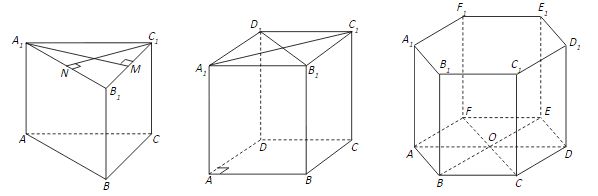
Если у основания прямой призмы лежит правильный многоугольник, то такая призма является правильной.
Теперь вспомним свойства, которыми обладает правильная призма.
Свойства правильной призмы
• Во-первых, всегда основаниями правильной призмы служат правильные многоугольники;
• Во-вторых, если рассматривать у правильной призмы боковые грани, то они всегда бывают равными прямоугольниками;
• В-третьих, если сравнивать размеры боковых ребер, то в правильной призме они всегда равны.
• В-четвертых, правильная призма всегда прямая;
• В-пятых, если же в правильной призмы боковые грани имеют форму квадратов, то такую фигуру, как правило, называют полуправильным многоугольником.
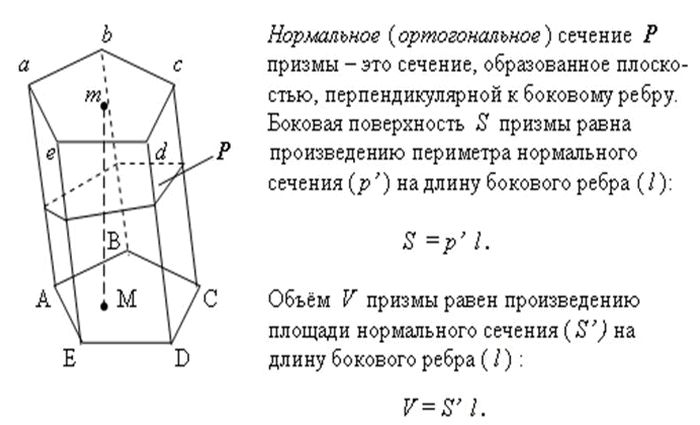
Сечение призмы
А теперь давайте рассмотрим сечение призмы:
Домашнее задание
А теперь давайте попробуем закрепить изученную тему с помощью решения задач.
Давайте нарисуем наклонную треугольную призму, у которой расстояние между ее ребрами будет равно: 3 см, 4 см и 5 см, а боковая поверхность этой призмы будет равна 60 см2. Имея такие параметры, найдите боковое ребро данной призмы.
Интересно знать
А вы знаете, что геометрические фигуры постоянно окружают нас не только на уроках геометрии, но и в повседневной жизни встречаются предметы, которые напоминают ту или иную геометрическую фигуру.

У каждого дома, в школе или на работе имеется компьютер, системный блок которого имеет форму прямой призмы.
Если вы возьмете в руки простой карандаш, то вы увидите, что основной частью карандаша, является призма.
Идя по центральной улице города, мы видим, что у нас под ногами лежит плитка, которая имеет форму шестиугольной призмы.
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
|















