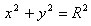Текущая версия на 12:00, 30 июля 2015

Гипермаркет знаний>>Математика>>Математика 8 класс. Полные уроки>>Геометрия: Уравнение окружности. Полные уроки

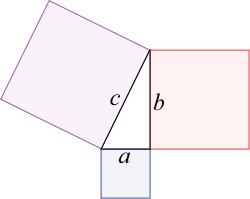
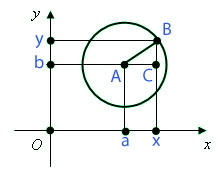
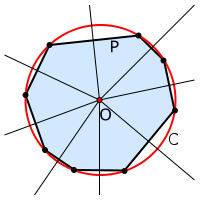
Тема урока

Уравнение окружности

План урока

1. Уравнение окружности.
2. Исторические данные.
3. Повторение пройденного материала.

Уравнение окружности

Самым простым из способов, представляющих уравнения окружности, является теорема Пифагора.

Теорема Пифагора:

Вы уже знаете, что теорема Пифагора имеет как геометрическую формулировку, так и алгебраическую.

Геометрическая формулировка звучит так:

В прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах.

Алгебраическая формулировка звучит так:

В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

Давайте возьмем окружность, центром которой является точка A (a; b) и радиус R. Теперь давайте на этой окружности возьмем произвольную точку В (x; y). В этом случае мы с вами можем применить теорему Пифагора.

В итоге, как видно с рисунка, мы с вами получили прямоугольный треугольник, который имеет стороны: АВ, ВС и СА.

В том случае, когда центр окружности расположен в начале координат, то есть, a = 0 и b = 0, то мы получаем уравнение окружности, которое принимает такой вид:

Обратно: любая точка В, координаты которой удовлетворяет данному уравнению окружности, принадлежат окружности.

Немного истории

А знаете ли вы, что оказывается термины «окружность» и «круг» получили свои названия еще во времена Древней Греции. Для древних греков окружность и круг были венцом совершенства, ведь они уже в те времена пришли к выводу, что окружность в каждой своей точке устроена таким образом, что позволяет ей двигаться самой по себе. Также они обратили внимание на то, что из всех фигур, которые имеют одинаковую длину периметра, только у круга наибольшая площадь.

Древние философы придавали огромное значение окружности, ведь она является одной из древнейших геометрических фигур. Если следовать учению Аристотеля, то все планеты и звезды нашей вселенной движутся по самой совершенной линии, которой является окружность. Да и еще на протяжении сотни лет ученые астрономы были уверены, что все планеты движутся по окружности. И лишь только в XVII веке учением Коперника, Галилея, Кеплера и Ньютона это суждение было опровергнуто.

Аристотель

Николай Коперник

Галилео Галилей

Иоганн Кеплер

Исаак Ньютон

Повторение ранее изученного материала

Даже в древние времена круглые предметы вызывали огромный интерес у человека, так как тогда отсутствовали какие-либо технические сооружения, и для постройки знаменитых египетских пирамид приходилось использовать бревна круглой формы. Немного позже для перемещения огромных глыб, вместо бревен стали использовать колеса, так как они были легче в использовании.

Геометрические примитивы

А теперь давайте вспомним, какие примитивные фигуры вы уже изучили и дадим им определения.

Вы уже знаете, что любой фигурой называют произвольное множество точек на плоскости.

К таким геометрическим фигурам можно отнести точку, прямую, отрезок, луч, треугольник, круг, квадрат и др.

Также вам известно, что точка и прямая являются основными геометрическими фигурами на плоскости. Но в геометрии этим фигурам не дается определения, и они являются неопределяемыми геометрическими фигурами на плоскости.

Как правило, точки обозначаются заглавными латинскими буквами: А, В, С, D …. А вот прямые, обозначаются латинскими строчными буквами: а, b, с, d ….

«Точка» является одним из основных понятий в геометрии, но определения она не имеет. По теории Евклида, точкой является то, что нельзя разделить.

«Прямая» также является одним из главных геометрических понятий. Она представляет собой линию, которая незамкнутая, не искривленная и протяженная с двух сторон, у которой поперечное сечение стремится к нулю, а продольная проекция на плоскость даёт точку.

«Треугольник» является также простейшей геометрической фигурой, которая имеет три стороны и три угла. Можно сказать, что это такая часть плоскости, которая ограничена тремя точками, и тремя отрезками, которые попарно соединяют эти точки.

«Прямоугольник» является параллелограммом, с четырьмя углами, каждый из которых равен 90 градусам.

«Окружность» - это такая геометрическая фигура, у которой каждая точка равноудалена от центра окружности.

Связь окружности с другими фигурами

Так как вы уже изучали тему «Окружность», то вам известно, что описанной окружностью многоугольника является такая окружность, которая охватывает все вершины этого многоугольника.

Если вы внимательно рассмотрите рисунок, то увидите, что центром пересечения серединных перпендикуляров окружности является точка О.

А вот вписанной в многоугольник окружностью называют такую окружность, которая расположена внутри данного многоугольника и которая касается всех прямых, проходящих через его стороны.

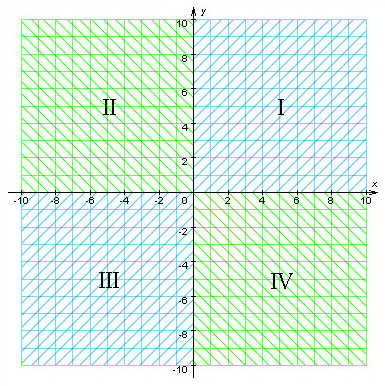
Прямоугольная система координат

Изображенная на рисунке система координат называется декартовой или прямоугольной. Первое свое название эта система координат получила благодаря имени своего создателя, а вторая, благодаря прямому углу, который равен 90°.

Окружность и круг

А теперь давайте с вами вспомним все определения, которые непосредственно касаются таких понятий, как «окружность» и «круг».

Окружностью называют такую замкнутую прямую линию, у которой все точки равноудалены от центра.

А кругом является та часть плоскости, которая ограниченная этой окружностью.

Но мы с вами также знаем, что каждая окружность имеет диаметр. Им называют отрезок, соединяющий две точки окружности. Диаметр проходит через центр этой окружности и является максимальным расстоянием между точками этой фигуры.

Радиус окружности делит диаметр пополам, а также соединяет центр окружности с любой его точкой.

В отличие от диаметра, хорда не проходит через центр окружности, а располагается около нее.

В окружности присутствует и такое понятие, как круговой сектор. Это часть круга, которая ограничивается дугой и двумя радиусами. Эти радиусы соединяют концы дуги с центром круга.

Ну и, как правило, в геометрии для построения окружности используют циркуль.

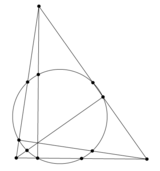
Интересный факт

Окружность девяти точек

Такой простой, на первый взгляд многоугольник, который является треугольник издавна не оставлял равнодушными многих ученых математиков. Уделил свое внимание этой фигуре и такой знаменитый математик, как Леонард Эйлер. Он вывел и доказал теорему окружности девяти точек. В геометрии треугольника это обозначает, что есть окружность, которая проходит через середины всех имеющихся сторон треугольника. Такая окружность получила название окружности «Эйлера», «Фейербаха» или окружности шести точек.

Окружностью девяти точек она называется благодаря следующей теореме:

В 1765 году Леонард Эйлер представил доказательство того, что основания высот и середины сторон расположены на одной окружности. Благодаря этому доказательству и появилось название «окружность шести точек».

Но это доказательство еще носит имя Карла Фейербаха, так как он первым его опубликовал в 1821 году вместе с теоремой, которой дал свое имя.