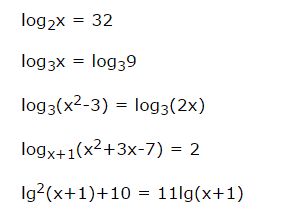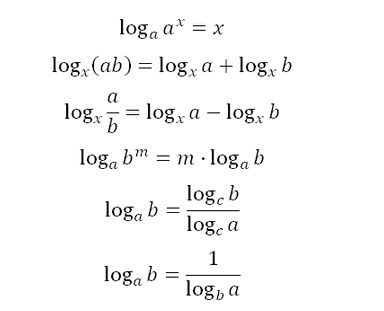|
|
|
| (3 промежуточные версии не показаны) | | Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 10 класс, урок, на Тему, Логарифмические уравнения</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 10 класс, урок, на Тему, Логарифмические уравнения, корни, логарифм, неравенства</metakeywords> |
| | | | |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 10 класс|Математика 10 класс]]>> Логарифмические уравнения''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 10 класс|Математика 10 класс]]>> Логарифмические уравнения''' |
| | | | |
| | + | <h2>Что такое логарифмическое уравнение?</h2> |
| | | | |
| | + | Логарифмическим уравнением называют такое уравнение, в котором неизвестная представлена под знаком логарифма. |
| | | | |
| - | '''§ 51. Логарифмические уравнения'''<br>Логарифмическими уравнениями называют уравнения вида [[Image:a10194.jpg]]<br>где а — положительное число, отличное от 1, и уравнения, сводящиеся к этому виду.<br>Опираясь на теорему 4 из § 50, согласно которой равенство [[Image:a10195.jpg]] справедливо тогда и только тогда, когда 1=8, мы можем сформулировать следующее утверждение.<br>
| + | То есть, если говорить более понятным языком, то в логарифмическом уравнении все неизвестные х, а также выражения с ними, расположены внутри логарифмов. |
| | | | |
| - | [[Image:a10196.jpg]]
| + | Теперь давайте рассмотрим примеры логарифмических уравнений: |
| | | | |
| - | На практике эту теорему применяют так: переходят от уравнения (1) к уравнению f(х) = g(х) (такой переход называют потенцированием), решают уравнение f(х)= g(х), а затем проверяют его корни по условиям f(х) >0, g(х) >0, определяющим область допустимых значений переменной (ОДЗ). Те корни уравнения f(х) = g(х), которые удовлетворяют этим условиям, являются корнями уравнения (1). Те корни уравнения f(х) =g(х), которые не удовлетворяют хотя бы одному из этих условий, объявляются посторонними корнями для уравнения (1).<br>'''Пример 1'''. Решить уравнение: [[Image:a10197.jpg]]<br>'''Решение'''.1) Потенцируя (т.е. освободившись от знаков логарифмов), получаем:
| + | <br> |
| | + | [[Image:10kl_Logarifm01.jpg|300x300px|логарифм]] |
| | + | <br> |
| | + | |
| | + | Если вы внимательно посмотрите на примере этих разнообразных уравнений, то заметите, что выражения с неизвестными х расположены, все без исключения, внутри логарифмов. |
| | | | |
| - | [[Image:a10198.jpg]]
| + | Но бывают такие случаи, когда в уравнении, внутри логарифмов не наблюдается присутствия х, а есть только числа. Например: |
| | | | |
| - | 2) Проверим наиденные корни по условиям: | + | х+2 = lg8+lg50 |
| | | | |
| - | [[Image:a10199.jpg]]<br>Значение x = 4 не удовлетворяет этой системе неравенств (достаточно заметить, что x = 4 не удовлетворяет второму неравенству системы), т.е. x = 4 — посторонний корень для заданного уравнения. Значение x =-3 удовлетворяет обоим неравенствам системы, а потому х = —3 — корень заданного уравнения.<br>Ответ: х = -3.<br>'''Пример 2.''' Решить уравнение:
| + | Если вам попалось такое уравнение, то можно сказать, что вам повезло. Ведь логарифм с числами - это какое-то число и чтобы решить такое уравнение, достаточно хорошо понимать свойства логарифмов. В этом случае не требуется особых ни знаний каких-то определенных правил, ни особых приемов. |
| | | | |
| - | [[Image:a10200.jpg]]<br>'''Решение'''. 1) Сначала надо преобразовать уравнение к виду (1). Для этого воспользуемся правилом: «сумма логарифмов равна логарифму произведения». Оно позволяет заменить выражение log<sub>2</sub>(х + 4)+ log<sub>2</sub>(2x + 3) выражением log<sup>2</sup>(х + 4)(2x: + 3). Тогда заданное уравнение можно переписать в виде: | + | <br> |
| | + | [[Image:10kl_Logarifm02.jpg|500x500px|логарифм]] |
| | + | <br> |
| | + | |
| | + | <h2>Как решать простейшие логарифмические уравнения?</h2> |
| | | | |
| - | [[Image:a10201.jpg]]<br>2) Потенцируя, получаем:
| + | Существует довольно много различных методов решения логарифмических уравнений. К таким способам относится такие своеобразные подходы, как разложение на множители, замена, потенцирование, а также работа с основаниями. |
| | | | |
| - | [[Image:a101202.jpg]]<br>3) Проверим найденные корни по условиям:
| + | Но какой бы способ решения логарифмического уравнения вы не выбрали, следует знать, что все решения этих уравнений сводятся к тому, что любое логарифмическое уравнение необходимо привести к его простейшему виду: |
| | | | |
| - | [[Image:a10203.jpg]]
| + | loga(f(x)) = loga(g(x)), |
| | | | |
| - | (обратите внимание: условия для проверки всегда определяют по заданному уравнению). Значение x = -1 удовлетворяет этой системе неравенств, а значение х = -5,5 не удовлетворяет (это посторонний корень).<br>Ответ: х = -1.<br>'''Замечание.''' Иногда удобнее использовать другой порядок ходов: сначала решить систему неравенств — в примере 2 решением системы неравенств будет интервал (-1,5, 0,5); это — область допустимых значений переменной (ОДЗ) или область определения уравнения. Затем найти корни x<sub>1</sub> = -1, х<sub>2</sub> = -5,5. И, наконец, сделать проверку найденных значений х, но уже не с помощью системы неравенств, а по найденной заранее области допустимых значений. В примере 2 значение x = -1 принадлежит интервалу (-1,5, 0,5), а значение x = -5,5 этому интервалу не принадлежит. Следовательно, х = -5,5 — посторонний корень, т.е. x = -1 — единственный корень заданного логарифмического уравнения.<br>'''Пример 3'''. Решить уравнение:
| + | После того, как вы свели уравнение к такому виду, можете приступать к решению уравнения без логарифмов: |
| | | | |
| - | [[Image:a10204.jpg]]
| + | f(x)=g(x). |
| | | | |
| - | '''Решение'''. Так как [[Image:a10205.jpg]] то заданное уравнение можно переписать в виде [[Image:a10206.jpg]]<br>Есть смысл ввести новую переменную y = lg х; тогда уравнение примет вид
| + | То есть, чтобы вам было еще более понятно, то следует запомнить, что весь процесс решения любого логарифмического уравнения сводится к тому, что необходимо перейти от уравнения с логарифмами к уравнению, где логарифмы отсутствуют. |
| | | | |
| - | [[Image:a10207.jpg]]
| + | В простых логарифмических уравнениях такой переход осуществляется довольно просто. |
| | + | Давайте рассмотрим этот процесс на примере. |
| | | | |
| - | Это значение удовлетворяет условию [[Image:a10208.jpg]] (посмотрите: у записанного выше рационального относительно у уравнения переменная содержится в знаменателе, а потому следует проверить, не обращается ли знаменатель в 0 при найденном значении переменной у).<br>Итак, у = 2. Но у = lg х, значит, нам осталось решить простейшее логарифмическое уравнение lg х = 2, откуда находим х = 100.<br>Ответ: х = 100.<br>Подведем некоторые итоги. Можно выделить три основных метода решения логарифмических уравнений.<br>1) Функционально-графический метод. Он основан на использовании графических иллюстраций или каких-либо свойств функций. Мы применяли этот метод в § 49.<br>2)Методпотенцирования. Он основан на теореме, полученной в начале параграфа. Мы применили этот метод в примерах 1 и 2.<br>3) Метод введения новой переменной. Мы применили этот метод в примере 3.<br>Завершая параграф, рассмотрим пример, в котором для решения уравнения используется еще один метод — метод логарифмирования, и пример решения системы логарифмических уравнений.<br>'''Пример 4.''' Решить уравнение [[Image:a10209.jpg]]<br>'''Решение.''' Возьмем от обеих частей уравнения логарифмы по основанию 5; зто — равносильное преобразование уравнения, поскольку обе его части принимают только положительные значения. Получим: [[Image:a10210.jpg]]<br>позволит переписать заданное уравнение в виде: (l - log<sub>5</sub>x) ■ log<sub>5</sub> х = -2. Замечаем, что «проявилась» новая переменная у = log<sub>5</sub> х, относительно которой уравнение принимает весьма простой вид: (1 - у)у = -2. Далее получаем:
| + | Вот мы с вами имеем простое логарифмическое уравнение: |
| | | | |
| - | [[Image:a10211.jpg]]<br>Но у = log<sub>5</sub> х, значит, нам осталось решить два уравнения:<br>log<sub>5</sub> x=2, log<sub>5</sub> x=-1. Из первого уравнения находим х = 5', т.е. х = 25; из второго уравнения находим x =5 , т.е.
| + | log3х = log39 |
| | | | |
| - | [[Image:a10212.jpg]]
| + | Чтобы получить уравнение без логарифмов, нам необходимо от них избавиться. В этом случае алгебра нам позволяет логарифмы убрать, и вот что в итоге мы получим: |
| | | | |
| - | '''Пример 5.''' Решить систему уравнений
| + | х = 9 |
| | | | |
| - | [[Image:a10213.jpg]]<br>'''Решение.''' 1) Преобразуем первое уравнение системы к более простому виду:
| + | Убрать логарифмы таким методом, является одним из основных способов решения логарифмических уравнений или неравенств. Такая своеобразная операция избавления от логарифмов называется потенцирование. |
| | | | |
| - | [[Image:a10214.jpg]]<br>2) Преобразуем второе уравнение системы к более простому виду:
| + | Но даже на такую ликвидацию логарифмов существуют определенные правила. |
| | | | |
| - | [[Image:a10215.jpg]]<br>3) Решим полученную систему уравнений:
| + | Без проблем и опасений убрать логарифмы можно в том случае, если: |
| | | | |
| - | [[Image:a10216.jpg]]<br>Подставив 2у вместо х во второе уравнение, получим [[Image:a10217.jpg]]<br>Соответственно из соотношения х = 2у находим х<sub>2</sub> = 4, х<sub>2</sub> = -2. 4) Осталось сделать проверку найденных пар (4; 2) и (-2; -1) с помощью условий, которые мы определяем, анализируя исходную систему уравнений:
| + | • Во-первых, они имеют одинаковые числовые основания;<br> |
| | + | • Во-вторых, что слева, что справа, логарифмы должны быть без всяких коэффициентов, то есть, находится в гордом одиночестве;<br> |
| | | | |
| - | [[Image:a10218.jpg]]<br>Пара (4; 2) удовлетворяет этим условиям, а пара (-2; -1) не удовлетворяет (например, она «не проходит» уже через первое условие 2х -у> 0).
| + | Но следует учесть, что при решении уравнений с логарифмами не всегда есть возможность от логарифма избавиться. Так, например, в уравнении: |
| | | | |
| - | '''Ответ:''' (4; 2).
| + | log3х = 2log3(3х-1) |
| | | | |
| | + | Убрать логарифм в этом случае не позволяет двойка, которая стоит справа, так как она является коэффициентом. |
| | | | |
| | + | А если рассмотреть следующий пример, то это уравнение также нельзя потенцировать, так как у него слева не наблюдается одинокого логарифма: |
| | | | |
| - | А.Г. Мордкович Алгебра 10 класс
| + | log3х+log3(х+1) = log3(3+х) |
| | | | |
| - | <br>
| + | Вот мы и пришли с вами к такому выводу, что убирать логарифмы можно только тогда, когда уравнение имеет соответственный вид: |
| | | | |
| - | [http://xvatit.com/relax/fun-videos/ '''<sub>Видео</sub>'''] <sub>по математике [[Математика|скачать]], домашнее задание, учителям и школьникам на помощь [[Гипермаркет знаний - первый в мире!|онлайн]]</sub>
| + | logа(.....) = logа(.....) |
| | | | |
| - | '''<u>Содержание урока</u>'''
| + | В этом уравнении в скобках могут быть любые выражения, но важно, чтобы после того, как мы уберем логарифм, у нас осталось более простое уравнение. |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] конспект урока '''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии
| + | |
| - |
| + | |
| - | '''<u>Практика</u>'''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников
| + | |
| - |
| + | |
| - | '''<u>Иллюстрации</u>'''
| + | |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа '''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты
| + | |
| - |
| + | |
| - | '''<u>Дополнения</u>'''
| + | |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] рефераты'''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие
| + | |
| - |
| + | |
| - | <u>Совершенствование учебников и уроков
| + | |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике'''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми
| + | |
| - |
| + | |
| - | '''<u>Только для учителей</u>'''
| + | |
| - | '''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки '''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения
| + | |
| - |
| + | |
| - |
| + | |
| - | '''<u>Интегрированные уроки</u>'''<u>
| + | |
| - | </u>
| + | |
| | | | |
| | + | <h2>Свойства логарифмов</h2> |
| | + | |
| | + | <br> |
| | + | [[Image:10kl_Logarifm03.jpg|400x400px|логарифм]] |
| | <br> | | <br> |
| | | | |
| - | Если у вас есть исправления или предложения к данному уроку, [http://xvatit.com/index.php?do=feedback напишите нам].
| + | <h2>Следует знать</h2> |
| | + | |
| | + | На этом уроке мы с вами рассмотрели решение простейших логарифмических уравнений и можем с уверенностью сказать, что никаких сложных преобразований мы не наблюдали. |
| | + | |
| | + | Но для успешного решения таких задач важно знать свойства логарифма и понимать основное логарифмическое тождество. |
| | | | |
| - | Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - [http://xvatit.com/forum/ Образовательный форум].
| + | Также, следует запомнить, что после того, как будет найден корень логарифмического уравнения, необходимо в обязательном порядке делать проверку полученных корней. |
Текущая версия на 12:08, 20 августа 2015
Гипермаркет знаний>>Математика>>Математика 10 класс>> Логарифмические уравнения
Что такое логарифмическое уравнение?
Логарифмическим уравнением называют такое уравнение, в котором неизвестная представлена под знаком логарифма.
То есть, если говорить более понятным языком, то в логарифмическом уравнении все неизвестные х, а также выражения с ними, расположены внутри логарифмов.
Теперь давайте рассмотрим примеры логарифмических уравнений:
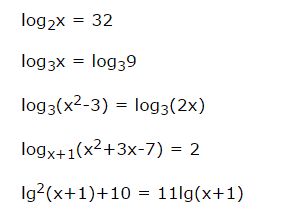
Если вы внимательно посмотрите на примере этих разнообразных уравнений, то заметите, что выражения с неизвестными х расположены, все без исключения, внутри логарифмов.
Но бывают такие случаи, когда в уравнении, внутри логарифмов не наблюдается присутствия х, а есть только числа. Например:
х+2 = lg8+lg50
Если вам попалось такое уравнение, то можно сказать, что вам повезло. Ведь логарифм с числами - это какое-то число и чтобы решить такое уравнение, достаточно хорошо понимать свойства логарифмов. В этом случае не требуется особых ни знаний каких-то определенных правил, ни особых приемов.

Как решать простейшие логарифмические уравнения?
Существует довольно много различных методов решения логарифмических уравнений. К таким способам относится такие своеобразные подходы, как разложение на множители, замена, потенцирование, а также работа с основаниями.
Но какой бы способ решения логарифмического уравнения вы не выбрали, следует знать, что все решения этих уравнений сводятся к тому, что любое логарифмическое уравнение необходимо привести к его простейшему виду:
loga(f(x)) = loga(g(x)),
После того, как вы свели уравнение к такому виду, можете приступать к решению уравнения без логарифмов:
f(x)=g(x).
То есть, чтобы вам было еще более понятно, то следует запомнить, что весь процесс решения любого логарифмического уравнения сводится к тому, что необходимо перейти от уравнения с логарифмами к уравнению, где логарифмы отсутствуют.
В простых логарифмических уравнениях такой переход осуществляется довольно просто.
Давайте рассмотрим этот процесс на примере.
Вот мы с вами имеем простое логарифмическое уравнение:
log3х = log39
Чтобы получить уравнение без логарифмов, нам необходимо от них избавиться. В этом случае алгебра нам позволяет логарифмы убрать, и вот что в итоге мы получим:
х = 9
Убрать логарифмы таким методом, является одним из основных способов решения логарифмических уравнений или неравенств. Такая своеобразная операция избавления от логарифмов называется потенцирование.
Но даже на такую ликвидацию логарифмов существуют определенные правила.
Без проблем и опасений убрать логарифмы можно в том случае, если:
• Во-первых, они имеют одинаковые числовые основания;
• Во-вторых, что слева, что справа, логарифмы должны быть без всяких коэффициентов, то есть, находится в гордом одиночестве;
Но следует учесть, что при решении уравнений с логарифмами не всегда есть возможность от логарифма избавиться. Так, например, в уравнении:
log3х = 2log3(3х-1)
Убрать логарифм в этом случае не позволяет двойка, которая стоит справа, так как она является коэффициентом.
А если рассмотреть следующий пример, то это уравнение также нельзя потенцировать, так как у него слева не наблюдается одинокого логарифма:
log3х+log3(х+1) = log3(3+х)
Вот мы и пришли с вами к такому выводу, что убирать логарифмы можно только тогда, когда уравнение имеет соответственный вид:
logа(.....) = logа(.....)
В этом уравнении в скобках могут быть любые выражения, но важно, чтобы после того, как мы уберем логарифм, у нас осталось более простое уравнение.
Свойства логарифмов
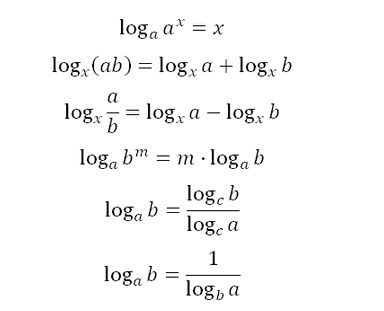
Следует знать
На этом уроке мы с вами рассмотрели решение простейших логарифмических уравнений и можем с уверенностью сказать, что никаких сложных преобразований мы не наблюдали.
Но для успешного решения таких задач важно знать свойства логарифма и понимать основное логарифмическое тождество.
Также, следует запомнить, что после того, как будет найден корень логарифмического уравнения, необходимо в обязательном порядке делать проверку полученных корней.
|