KNOWLEDGE HYPERMARKET

Модуль числа. Полные уроки
 
(7 промежуточных версий не показаны.)
Строка 1: Строка 1:
'''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 6 класс. Полные уроки|Математика 6 класс. Полные уроки]]>>Математика: Модуль числа. Полные уроки'''  
'''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 6 класс. Полные уроки|Математика 6 класс. Полные уроки]]>>Математика: Модуль числа. Полные уроки'''  
-
 
-
----
 
<metakeywords>Гипермаркет знаний, Математика, 6 класс, модуль числа</metakeywords>  
<metakeywords>Гипермаркет знаний, Математика, 6 класс, модуль числа</metakeywords>  
-
== Тема урока:  ==
+
<h2>Цели урока</h2>
-
<br>  
+
• Познакомить школьников с таким математическим понятием, как модуль числа;<br>
 +
• Научить школьников навыкам нахождения модулей чисел;<br>
 +
• Закрепить изученный материал с помощью выполнения различных заданий;<br>
-
*<u>'''Модуль числа'''</u><br>
+
<h2>Задачи</h2>
-
<br>  
+
• Закрепить знания детей о модуле числа;<br>
 +
• С помощью решения тестовых заданий проверить, как усвоили ученики изученный материал;<br>
 +
• Продолжать прививать интерес к урокам математики;<br>
 +
• Воспитывать у школьников логическое мышление, любознательность и усидчивость.<br>
-
== Тип урока:  ==
+
<h2>План урока</h2>
-
<br>изучение и первичное усвоение нового материала
+
1. Общие понятия и определение модуля числа.<br>
 +
2. Геометрический смысл модуля.<br>
 +
3. Модуль числа его свойства.<br>
 +
4. Решение уравнений и неравенств, которые содержат модуль числа.<br>
 +
5. Историческая справка о термине «модуль числа».<br>
 +
6. Задание на закрепление знаний пройденной темы.<br>
 +
7. Домашнее задание.<br>
-
== Цели урока:  ==
+
<h2>Общие понятия о модуле числа</h2>
-
<br>• формирование понятия «модуль», умения находить модуль числа. <br> • развитие логического мышления, математической речи, сознательного восприятия учебного материала. <br> • Углубить знания по геометрии, изучить историю происхождения. <br> • Развивающие – развить внимание учащихся, усидчивость, настойчивость, логическое мышление, математическую речь. <br> • Воспитательные - посредством урока воспитывать внимательное отношение друг к другу, прививать умение слушать товарищей, взаимовыручке, самостоятельность.  
+
Модулем числа принято называть само число, если оно не имеет отрицательного значения, или это же число отрицательное, но с противоположным знаком.
-
== Задачи урока: ==
+
То есть, модулем неотрицательного действительного числа a является само это число:
-
<br> • узнать, что такое модуль <br> • научиться использовать это понятие при решении задач <br> • проверить умение учащихся решать задачи.
+
|а| = а
-
== План урока: ==
+
А, модулем отрицательного действительного числа х будет противоположное число:
-
<br> 1. Введение. <br> 2. Теоретическая часть <br> 3. Практическая часть. <br> 4. Домашнее задание. <br> 5. Интересные факты <br> 6. Вывод
+
|а| = - а
-
== Введение  ==
+
В записи это будет выглядеть так:
-
Сегодня на уроке предстоит сделать немало открытий. Чтобы узнать тему урока, решите ребус.  
+
<br>
 +
[[Image:6kl_Modyl01.jpg|400x400px|модуль]]
 +
<br>
 +
 +
Для более доступного понимания приведем пример. Так, например, модулем числа 3 будет 3, и также модулем числа -3, является 3.
-
[[Image:052012img1.jpg]]
+
Из этого следует, что под модулем числа подразумевается абсолютная величина, то есть, ее абсолютное значение, но без учета его знака. Если говорить еще более просто, то необходимо от числа отбросить знак.
-
На рисунке зашифровано слово «модуль». Итак, тема урока – «Модуль числа». В переводе с латинского modulus – «мера». Считают, что термин предложил использовать Котс, ученик Ньютона. Лейбниц тоже использовал эту функцию, которую называл модулем и обозначал: mol x. Общепринятое обозначение абсолютной величины введено в 1841 году Вейерштрассом. Для комплексных чисел это понятие ввели Коши и Арган в начале XIX века.  
+
Обозначаться и выглядеть модуль числа может так: |3|, |х|, |а| и т.д.
-
== Теоретическая часть  ==
+
Так, например, модуль числа 3 обозначается |3|.
-
=== Определения и основные факты  ===
+
Также, следует помнить, что модуль числа никогда не бывает отрицательным: |a|≥ 0.
-
Как известно, каждое действительное число можно отождествить с точкой на числовой прямой. Поскольку про каждую отличную от нуля точку можно сказать, лежит она левее нуля или правее, а также измерить расстояние от этой точки до нуля, мы можем связать с каждым действительным числом две величины: его знак и его модуль. А именно, если точка, изображающая число х, лежит левее нуля, то говорят, что знак числа х отрицателен, а если правее нуля, то говорят, что знак числа х положителен; число 0 знака не имеет. Модуль числа х, равный расстоянию от точки, изображающей число х, до нуля можно измерить для всех действительных чисел. Например, число 3 положительно, а его модуль равен 3, число -5 отрицательно, а его модуль равен 5; модуль нуля равен нулю. Как мы видим, модуль положительного числа равен самому этому числа. Модуль отрицательного числа равен "минус"-этому числу, то есть противоположному числу; например, модуль числа -5 равен –(–5)=5. Таким образом, каждое действительно число х можно записать в виде х =знак х модуль х.  
+
|5| = 5, |-6| = 6, |-12,45| = 12,45 и т.д.
-
[[Image:052012img2.jpg|475x316px|052012img2.jpg]]
+
<h2>Геометрический смысл модуля</h2>
-
Например: Расстояние до точки М (-6) от начала отсчета O равно 6 единичным отрезкам. Число 6 называют модулем числа -6. Пишут: |-6| = 6.  
+
Модулем числа называют расстояние, которое измеряется в единичных отрезках от начала координат до точки. В этом определении раскрывается модуль с геометрической точки зрения.  
-
[[Image:052012img3.jpg]]
+
Возьмем координатную прямую и обозначим на ней две точки. Пускай этим точкам будут соответствовать такие числа, как −4 и 2.
-
'''Модулем числа а называют расстояние (в единичных отрезках) от начала координат до точки А (а).'''
+
<br>
 +
[[Image:6kl_Modyl02.jpg|500x500px|модуль]]
 +
<br>
 +
 +
Теперь давайте обратим внимание на данный рисунок. Мы видим, что обозначенная на координатной прямой точка А соответствует числу -4 и если вы внимательно посмотрите, то увидите, что эта точка находится от точки отсчета 0 на расстоянии 4 единичных отрезков. Отсюда следует, что длина отрезка OA равняется четырем единицам. В этом случае, длина отрезка ОА, то есть число 4 будет модулем числа -4.
-
Модуль числа 5 равен 5, так как точка В (5) удалена от начала отсчета на 5 единичных отрезков. Пишут: |5| = 5. Модуль числа 0 равен 0, так как точка с координатой 0 совпадает с началом отсчета O, т.е. удалена от нее на 0 единичных отрезков (см. рис. 63). Пишут: |0| = 0. Модуль числа не может быть отрицательным. Для положительного числа и нуля он равен самому числу, а для отрицательного — противоположному числу. Противоположные числа имеют равные модули: |-а| = |а|.  
+
Обозначается и записывается в данном случае модуль числа таким образом: |−4| = 4.
-
Например,
+
Читать эти символы следует таким образом: модуль числа минус четыре равен четырём.
-
[[Image:052012img4.jpg]]<br>
+
Теперь возьмем, и на координатной прямой обозначим точку В.  
-
Итак, '''абсолю́тная величина́ или мо́дуль, '''обозначается |x|. В случае вещественного аргумента — непрерывная кусочно-линейная функция, определённая следующим образом:
+
Эта точка В будет соответствовать числу +2, и находится она, как мы видим, от начала отсчета на расстоянии двух единичных отрезков. Из этого следует, что длина отрезка OB равняется двум единицам. В этом случае число 2 будет модулем числа +2.
-
[[Image:052012img5.jpg]]
+
В записи это будет выглядеть так: |+2| = 2 или |2| = 2.
-
Обобщением этого понятия является модуль комплексного числа , также иногда называемый абсолютной величиной. Он определяется по формуле:
+
А теперь подведем итог. Если мы с вами возьмем какое-то неизвестное число а и обозначим его на координатной прямой точкой А, то в этом случае расстояние от точки A до начала отсчёта, то есть длинна отрезка ОА, как раз и является модулем числа «a».
-
[[Image:052012img6.jpg]]
+
В записи это будет выглядеть так: |a| = OA.
-
=== Свойства модуля  ===
+
<h2>Модуль числа его свойства</h2>
-
Следующие свойства справедливы для всех действительных значений входящих в них переменных.
+
А теперь давайте попробуем выделить свойства модуля, рассмотреть всевозможные случаи и записать их с помощью буквенных выражений:
-
1) [[Image:052012img7.jpg|47x17px|052012img7.jpg]], причем |a|=0 тогда и только тогда, когда a=0. <br>  
+
• Во-первых, модулем числа является число неотрицательное, а значит модуль положительного числа, равен самому числу: |a| = a, если a > 0;<br>
-
2) |-a|=|a| <br>  
+
• Во-вторых, модули, которые состоят из противоположных чисел, равны: |а| = |–а|. То есть это свойство говорит нам о том, что противоположные числа всегда имеют равные модули, та как на координатной прямой, хотя они и имеют противоположные числа, но они находятся на одинаковом расстоянии от точки отсчета. Из этого следует, что и модули этих противоположных чисел равны.<br>
-
3) |ab|=|a||b|; в частности, |a|<sup>2</sup><sup></sup>=|a<sup>2</sup>|=a<sup>2</sup>. <br>
+
• В-третьих, модуль нуля равняется нулю в том случае, если это число является нулем: |0| = 0, если a = 0. Здесь можно с уверенностью сказать, что модулем нуля является ноль по определению, так как ему соответствует начало отсчета координатной прямой.
-
4) [[Image:052012img8.jpg|498x23px|052012img8.jpg]] <br>  
+
• Четвертым свойством модуля является то, что модуль произведения двух чисел равен произведению модулей этих чисел. Теперь подробнее рассмотрим, что это значит. Если следовать определению, то мы с вами знаем, что модуль произведения чисел a и b будет равен a•b, или −(a•b), если, а•в ≥ 0, или же – (а•в), если, а•в больше 0. В записи это будет выглядеть так: |а • b| = |а| • |b|.<br>
-
5) [[Image:052012img9.jpg|74x21px|052012img9.jpg]]. <br>  
+
• Пятым свойством является то, что модуль частного от деления чисел равен отношению модулей этих чисел: |а : b| = |а| : |b|.<br>
-
6) |a|=max{a, -a}; в частности&nbsp;[[Image:052012img10.jpg|448x22px|052012img10.jpg]] <br>
+
И следующие свойства модуля числа:
-
 
+
-
7) [[Image:052012img11.jpg|117x37px|052012img11.jpg]]
+
-
 
+
-
Видео: {{#ev:youtube|5wmvmhZQduM}}
+
-
 
+
-
== Практическая часть  ==
+
-
 
+
-
=== [[Image:052012img12.jpg]] ===
+
-
 
+
-
 
+
-
 
+
-
[[Image:052012img13.jpg]]
+
-
 
+
-
 
+
-
 
+
-
[[Image:052012img14.jpg]]
+
-
 
+
-
=== Пример 1.1  ===
+
-
 
+
-
Решить уравнение .
+
-
 
+
-
*РЕШЕНИЕ. Преобразуем левую часть уравнения: . Поскольку каждое из полученных слагаемых неотрицательно при всех значениях , рассматриваемая сумма также всегда неотрицательно, причем равна нулю тогда и только тогда, когда каждое из слагаемых равно нулю. Таким образом, исходное уравнение равносильно уравнению .
+
-
*ОТВЕТ: .
+
-
 
+
-
Графики функций – х и |х| выглядят следующим образом. Функция – х разрывна в нуле и нечетна. Функция |х| непрерывна на всей числовой прямой и четна. При отрицательных значениях переменной она убывает. а при положительных - возрастает.
+
 +
<br>
 +
[[Image:6kl_Modyl03.jpg|700x500px|модуль]]
<br>  
<br>  
-
=== Пример 1.2  ===
+
<h2>Решение уравнений и неравенств, которые содержат модуль числа</h2>
-
При каждом значении параметра найти число точек пересечения кривых и .  
+
Приступив к решению задач, которые имеют модуль числа, следует помнить, что чтобы решить такое задание, необходимо раскрыть знак модуля, используя знания свойств, которым эта задача соответствует.  
-
*РЕШЕНИЕ. Изобразим на плоскости данные кривые. первая из них получается с помощью сжатия и, быть может, симметрии относительно оси графика функции , а второе уравнение задает окружность радиуса с центром в точке . При кривая лежит в первой и второй четвертях включая ось (при кривая совпадает с осью ), а окружность - в третьей и четвертой, не имея общих точек с осью . Следовательно, в этом случае данные кривые не пересекаются.
+
'''Задание 1'''
-
Пусть теперь . При малых по модулю значениях параметра у рассматриваемых кривых общих точек по-прежнему не будет. Затем при уменьшении параметра , произойдет касание (этот момент изображен на рисунке),  
+
Так, к примеру, если под знаком модуля стоит выражение, которое зависит от переменной, то раскрывать модуль следует в соответствии с определением:
-
<br> а при всех меньших значениях этого параметра будет ровно четыре общие точки. Остается лишь найти то значение параметра , при котором произойдет касание. Проведя радиус, получим египетский треугольник (то есть треугольник со сторонами , , ), из которого нетрудно найти угловой коэффициент соответствующей полупрямой: .  
+
<br>
 +
[[Image:6kl_Modyl04.jpg|400x400px|модуль]]
 +
<br>
 +
 +
Конечно же, при решении задач бывают случаи, когда модуль раскрывается однозначно. Если, например, взять<br>[[Image:6kl_Modyl05.jpg|500x500px|модуль]]<br>, здесь мы видим, что такое выражение под знаком модуля неотрицательно при любых значениях х и у.  
-
*ОТВЕТ: При число точек пересечения равно четырем, при - двум. а при точки пересечения отсутствуют.
+
Или, же для примера берем<br>[[Image:6kl_Modyl06.jpg|500x500px|модуль]]<br>, мы видим, что это выражение под модулем не положительно при любых значениях z.  
-
=== Пример 1.3  ===
+
'''Задание 2'''
-
Какая геометрическая фигура задается уравнением &nbsp;? Сделать чертеж.  
+
Перед вами изображена координатная прямая. На этой прямой необходимо отметить числа, модуль которых будет равен 2.
-
*РЕШЕНИЕ. Нетрудно видеть, что вместе с каждой своей точкой наша фигура содержит также точки , , . Значит, нам достаточно изобразить часть этой фигуры, лежащую в первой четверти, а затем отразить полученную кривую относительно обеих осей и начала координат.
+
<br>
 +
[[Image:6kl_Modyl07.jpg|500x500px|модуль]]
 +
<br>
 +
 +
'''Решение'''
-
Итак, пусть и . Тогда исходное уравнение принимает вид . Значит, лежащей в первой четверти частью фигуры является соответствующий отрезок прямой . произведя все указанные отражения этого отрезка, получим четырехугольник с равными перпендикулярными диагоналями, то есть квадрат.  
+
В первую очередь, мы должны начертить координатную прямую. Вам уже известно, что для этого, вначале на прямой необходимо выбрать начало отсчета, направление и единичный отрезок. Далее, нам нужно от начала отсчета поставить точки, которые равны расстоянию двух единичных отрезков.
-
*ОТВЕТ: квадрат.
+
Как видим, таких точек на координатной прямой две, одна из которых соответствует числу -2, а другая числу 2.
-
<br>  
+
<h2>Историческая справка о модуле числа</h2>
-
=== Тест «Модуль числа»  ===
+
Термин «модуль» произошел от латинского названия modulus, что в переводе обозначает слово «мера». Ввел в обращение этот термин английский математик Роджер Котес. А вот знак модуля был введен благодаря немецкому математику Карлу Вейерштрассу. При написании модуль обозначается с помощью такого символа: | |.
-
==== Вариант 1  ====
+
<h2>Вопросы на закрепление знаний материала</h2>
-
1. Найдите значение выражения |х|, если х = – 2,5.
+
На сегодняшнем уроке мы с вами познакомились с таким понятием, как модуль числа, а теперь давайте проверим, как вы усвоили эту тему, ответив на поставленные вопросы:
-
А) – 2,5 и 2,5; <br> Б) 2,5; <br> С) – 2,5  
+
1. Как называется число, которое противоположно положительному числу?<br>
 +
2. Какое название носит число, которое противоположно отрицательному числу?<br>  
 +
3. Назовите число, которое является противоположным нулю. Существует ли такое число?<br>
 +
4. Назовите то число, которое не может являться модулем числа.<br>
 +
5. Дайте определение модулю числа.<br>
-
2. Вставьте вместо точек нужные по смыслу слова: «Модуль отрицательного числа есть число …&nbsp;»
+
<h2>Домашнее задание</h2>
-
А) ему противоположное; <br> В) нуль; <br> С) отрицательное.
+
1. Перед вами изображены числа, которые вам нужно расположить в порядке убывания модулей. Если вы правильно выполните задание, то узнаете фамилию человека, который впервые ввел в математику термин «модуль».<br>
-
 
+
-
3. Выберите верные равенства:
+
-
 
+
-
1) |– 5| = 5; <br> 2) |– 3| = – 3; <br> 3) |4| = 4.  
+
-
 
+
-
А) 1; <br> В) 1 и 2; <br> С) 2 и 3; <br> D) 1 и 3; <br> Е) Все.
+
-
 
+
-
4. Известно, что |– а| = 16. Чему равен |а|?
+
-
 
+
-
А) – 16; <br> В) 16 и – 16; <br> С) 16.
+
-
 
+
-
5. Из чисел:
+
-
 
+
-
1) – 5,8; <br> 2) <br> 3) 0; <br> 4) – 7,35 выберите то, у которого бoльший модуль
+
-
 
+
-
А) 4; <br> В) 3; <br> С) 2; <br> D) 1.
+
-
 
+
-
6. При каких значениях х верно равенство |х| = 5?
+
-
 
+
-
А) – 5 и 5; <br> В) 5; <br> С) – 5; <br> D) Таких чисел нет.
+
-
 
+
-
7. Укажите верные неравенства
+
-
 
+
-
1) |– 50| &lt; |30|; <br> 2) |1,5| &gt; |– 0,9|; <br> 3) |13| &lt; |– 13|.
+
-
 
+
-
А) 1; <br> В) 3; <br> С) 1 и 3; <br> D) 2; <br> Е) Все.
+
-
 
+
-
8. Найдите расстояние от точки А (– 35,8) до начала отсчёта.
+
-
 
+
-
А) 35,8; <br> В) 38,5 и – 38,5; <br> С) 0; D) – 3,5.
+
-
 
+
-
==== Вариант 2  ====
+
-
 
+
-
1.Найдите значение выражения |х|, если х = – 4,3.
+
-
 
+
-
А) 4,3; <br> Б) – 4,3; <br> С) 4,3 и – 4,3.
+
-
 
+
-
2. Вставьте вместо точек нужные по смыслу слова: «Модуль положительного числа есть число …&nbsp;»
+
-
 
+
-
А) само это число; <br> В) отрицательное; <br> С) нуль.
+
-
 
+
-
3. Выберите верные равенства:
+
-
 
+
-
1) |– 9| = – 9; <br> 2) |– 6| = 6; <br> 3) |– 7| = 7.
+
-
 
+
-
А) 2 и 3; <br> В) 1 и 2; <br> С) 1 и 3; <br> D) 3; <br> Е) Все.
+
-
 
+
-
4. Известно, что |– b| = 10. Чему равен |b|?
+
-
 
+
-
А) 10; <br> В) – 10 и 10; <br> С) – 10.
+
-
 
+
-
5. Из чисел:
+
-
 
+
-
1) – 6,8; <br> 2) <br> 3) 10; <br>
+
-
 
+
-
4) – 11, 5 выберите то, у которого бoльший модуль.
+
-
 
+
-
А) 4; <br> В) 2; <br> С) 1; <br> D) 3.
+
-
 
+
-
6. При каких значениях х верно равенство | х | = 6?
+
-
 
+
-
А) 6; <br> В) – 6; <br> С) – 6 и 6; <br> D) Таких чисел нет.
+
-
 
+
-
7. Укажите верные неравенства
+
-
 
+
-
1) |– 60| &lt; |40|; <br> 2) |1,2| &gt; |– 0,12|; <br> 3) |– 15| &gt; |– 15|.
+
-
 
+
-
А) 1; <br> В) 2; <br> С) 3; <br> D) 1 и 2; <br> Е) Все.
+
-
 
+
-
8. Найдите расстояние от точки В (– 102,5) до начала отсчёта.
+
-
 
+
-
А) 0; <br> В) – 102,5; <br> С) 102,5; <br> D) 102,5 и – 102,5.
+
-
 
+
-
== Домашнее задание ==
+
-
 
+
-
1. Упростить выражение , если a &lt; 0. <br>2. Вычислить .
+
-
 
+
-
== Интересные факты  ==
+
-
 
+
-
Поскольку функция «модуль числа» вычисляется достаточно просто (только сравнениями и присваиванием), то обычно она входит в стандартный список функций во все языки программирования. Например, в Pascal есть функция abs(x), а в C fabs(x) для вещественного типа.
+
-
 
+
-
== Вывод  ==
+
-
 
+
-
Модулем неотрицательного действительного числа х называют само это число: |х| = х Модулем отрицательного действительного числа х называют противоположное число: |х| = - х Это записывают так:
+
-
 
+
-
[[Image:052012img5.jpg]]
+
-
 
+
-
----
+
-
 
+
-
'''Список использованных источников:'''<br> 1. Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 2002. — Т. 1.<br> 2. «Новейший справочник школьника» «ДОМ XXI век» 2008 г. <br> 3. Конспект урока на тему "Модуль числа" Автор: Петрова В. П., учитель математики (5-9 класс), г. Киев
+
-
 
+
-
----
+
-
 
+
-
'''Над уроком работали: '''<br> Паутинка А.В. <br> Петрова В.П.  
+
-
 
+
-
<br>  
+
-
----
+
<br>
 +
[[Image:6kl_Modyl08.jpg|500x500px|модуль]]
 +
<br>
-
Поставить вопрос о современном образовании, выразить идею или решить назревшую проблему Вы можете на [http://xvatit.com/forum/ '''Образовательном форуме'''], где на международном уровне собирается образовательный совет свежей мысли и действия. Создав [http://xvatit.com/club/blogs/ '''блог,'''] Вы не только повысите свой статус, как компетентного преподавателя, а и сделаете весомый вклад в развитие школы будущего. [http://xvatit.com/school/guild/ '''Гильдия Лидеров Образования'''] открывает двери для специалистов&nbsp; высшего ранга и приглашает к сотрудничеству в направлении создания лучших в мире школ.<br>  
+
2. Начертите координатную прямую и найдите расстояние от М(-5) и К (8) до начала отсчета.<br>
[[Category:Математика_6_класс]]
[[Category:Математика_6_класс]]

Текущая версия на 20:01, 31 августа 2015

Гипермаркет знаний>>Математика>>Математика 6 класс. Полные уроки>>Математика: Модуль числа. Полные уроки

Содержание

Цели урока

• Познакомить школьников с таким математическим понятием, как модуль числа;
• Научить школьников навыкам нахождения модулей чисел;
• Закрепить изученный материал с помощью выполнения различных заданий;

Задачи

• Закрепить знания детей о модуле числа;
• С помощью решения тестовых заданий проверить, как усвоили ученики изученный материал;
• Продолжать прививать интерес к урокам математики;
• Воспитывать у школьников логическое мышление, любознательность и усидчивость.

План урока

1. Общие понятия и определение модуля числа.
2. Геометрический смысл модуля.
3. Модуль числа его свойства.
4. Решение уравнений и неравенств, которые содержат модуль числа.
5. Историческая справка о термине «модуль числа».
6. Задание на закрепление знаний пройденной темы.
7. Домашнее задание.

Общие понятия о модуле числа

Модулем числа принято называть само число, если оно не имеет отрицательного значения, или это же число отрицательное, но с противоположным знаком.

То есть, модулем неотрицательного действительного числа a является само это число:

|а| = а

А, модулем отрицательного действительного числа х будет противоположное число:

|а| = - а

В записи это будет выглядеть так:


модуль

Для более доступного понимания приведем пример. Так, например, модулем числа 3 будет 3, и также модулем числа -3, является 3.

Из этого следует, что под модулем числа подразумевается абсолютная величина, то есть, ее абсолютное значение, но без учета его знака. Если говорить еще более просто, то необходимо от числа отбросить знак.

Обозначаться и выглядеть модуль числа может так: |3|, |х|, |а| и т.д.

Так, например, модуль числа 3 обозначается |3|.

Также, следует помнить, что модуль числа никогда не бывает отрицательным: |a|≥ 0.

|5| = 5, |-6| = 6, |-12,45| = 12,45 и т.д.

Геометрический смысл модуля

Модулем числа называют расстояние, которое измеряется в единичных отрезках от начала координат до точки. В этом определении раскрывается модуль с геометрической точки зрения.

Возьмем координатную прямую и обозначим на ней две точки. Пускай этим точкам будут соответствовать такие числа, как −4 и 2.


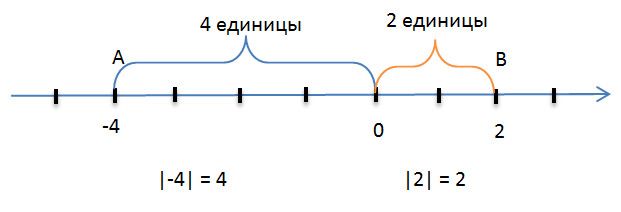
модуль

Теперь давайте обратим внимание на данный рисунок. Мы видим, что обозначенная на координатной прямой точка А соответствует числу -4 и если вы внимательно посмотрите, то увидите, что эта точка находится от точки отсчета 0 на расстоянии 4 единичных отрезков. Отсюда следует, что длина отрезка OA равняется четырем единицам. В этом случае, длина отрезка ОА, то есть число 4 будет модулем числа -4.

Обозначается и записывается в данном случае модуль числа таким образом: |−4| = 4.

Читать эти символы следует таким образом: модуль числа минус четыре равен четырём.

Теперь возьмем, и на координатной прямой обозначим точку В.

Эта точка В будет соответствовать числу +2, и находится она, как мы видим, от начала отсчета на расстоянии двух единичных отрезков. Из этого следует, что длина отрезка OB равняется двум единицам. В этом случае число 2 будет модулем числа +2.

В записи это будет выглядеть так: |+2| = 2 или |2| = 2.

А теперь подведем итог. Если мы с вами возьмем какое-то неизвестное число а и обозначим его на координатной прямой точкой А, то в этом случае расстояние от точки A до начала отсчёта, то есть длинна отрезка ОА, как раз и является модулем числа «a».

В записи это будет выглядеть так: |a| = OA.

Модуль числа его свойства

А теперь давайте попробуем выделить свойства модуля, рассмотреть всевозможные случаи и записать их с помощью буквенных выражений:

• Во-первых, модулем числа является число неотрицательное, а значит модуль положительного числа, равен самому числу: |a| = a, если a > 0;

• Во-вторых, модули, которые состоят из противоположных чисел, равны: |а| = |–а|. То есть это свойство говорит нам о том, что противоположные числа всегда имеют равные модули, та как на координатной прямой, хотя они и имеют противоположные числа, но они находятся на одинаковом расстоянии от точки отсчета. Из этого следует, что и модули этих противоположных чисел равны.

• В-третьих, модуль нуля равняется нулю в том случае, если это число является нулем: |0| = 0, если a = 0. Здесь можно с уверенностью сказать, что модулем нуля является ноль по определению, так как ему соответствует начало отсчета координатной прямой.

• Четвертым свойством модуля является то, что модуль произведения двух чисел равен произведению модулей этих чисел. Теперь подробнее рассмотрим, что это значит. Если следовать определению, то мы с вами знаем, что модуль произведения чисел a и b будет равен a•b, или −(a•b), если, а•в ≥ 0, или же – (а•в), если, а•в больше 0. В записи это будет выглядеть так: |а • b| = |а| • |b|.

• Пятым свойством является то, что модуль частного от деления чисел равен отношению модулей этих чисел: |а : b| = |а| : |b|.

И следующие свойства модуля числа:


модуль

Решение уравнений и неравенств, которые содержат модуль числа

Приступив к решению задач, которые имеют модуль числа, следует помнить, что чтобы решить такое задание, необходимо раскрыть знак модуля, используя знания свойств, которым эта задача соответствует.

Задание 1

Так, к примеру, если под знаком модуля стоит выражение, которое зависит от переменной, то раскрывать модуль следует в соответствии с определением:


модуль

Конечно же, при решении задач бывают случаи, когда модуль раскрывается однозначно. Если, например, взять
модуль
, здесь мы видим, что такое выражение под знаком модуля неотрицательно при любых значениях х и у.

Или, же для примера берем
модуль
, мы видим, что это выражение под модулем не положительно при любых значениях z.

Задание 2

Перед вами изображена координатная прямая. На этой прямой необходимо отметить числа, модуль которых будет равен 2.


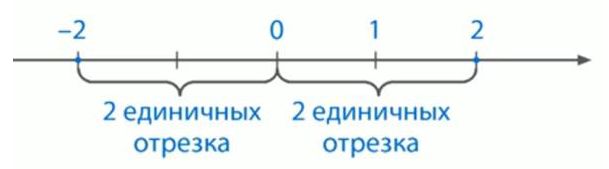
модуль

Решение

В первую очередь, мы должны начертить координатную прямую. Вам уже известно, что для этого, вначале на прямой необходимо выбрать начало отсчета, направление и единичный отрезок. Далее, нам нужно от начала отсчета поставить точки, которые равны расстоянию двух единичных отрезков.

Как видим, таких точек на координатной прямой две, одна из которых соответствует числу -2, а другая числу 2.

Историческая справка о модуле числа

Термин «модуль» произошел от латинского названия modulus, что в переводе обозначает слово «мера». Ввел в обращение этот термин английский математик Роджер Котес. А вот знак модуля был введен благодаря немецкому математику Карлу Вейерштрассу. При написании модуль обозначается с помощью такого символа: | |.

Вопросы на закрепление знаний материала

На сегодняшнем уроке мы с вами познакомились с таким понятием, как модуль числа, а теперь давайте проверим, как вы усвоили эту тему, ответив на поставленные вопросы:

1. Как называется число, которое противоположно положительному числу?
2. Какое название носит число, которое противоположно отрицательному числу?
3. Назовите число, которое является противоположным нулю. Существует ли такое число?
4. Назовите то число, которое не может являться модулем числа.
5. Дайте определение модулю числа.

Домашнее задание

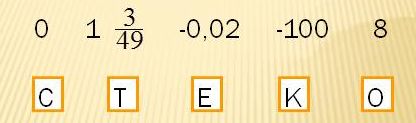
1. Перед вами изображены числа, которые вам нужно расположить в порядке убывания модулей. Если вы правильно выполните задание, то узнаете фамилию человека, который впервые ввел в математику термин «модуль».


модуль

2. Начертите координатную прямую и найдите расстояние от М(-5) и К (8) до начала отсчета.

Источник — «http://edufuture.biz/index.php?title=%D0%9C%D0%BE%D0%B4%D1%83%D0%BB%D1%8C_%D1%87%D0%B8%D1%81%D0%BB%D0%B0._%D0%9F%D0%BE%D0%BB%D0%BD%D1%8B%D0%B5_%D1%83%D1%80%D0%BE%D0%BA%D0%B8»
Предмети > Математика > Математика 6 класс

Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки

©  Автор системы образования 7W и Гипермаркета Знаний - Владимир Спиваковский

При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов - гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.

Разработка - Гипермаркет знаний 2008-

Ждем Ваши замечания и предложения на email:
По вопросам рекламы и спонсорства пишите на email: