Текущая версия на 20:01, 31 августа 2015Гипермаркет знаний>>Математика>>Математика 6 класс. Полные уроки>>Математика: Модуль числа. Полные уроки
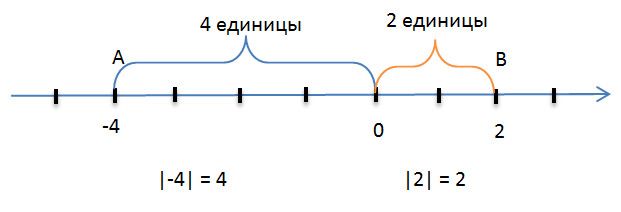
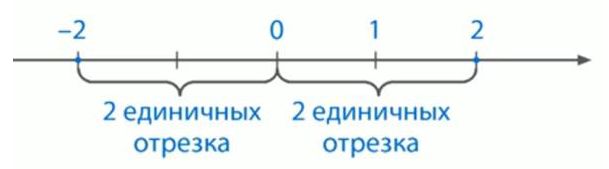
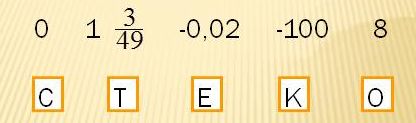
Цели урока• Познакомить школьников с таким математическим понятием, как модуль числа; Задачи• Закрепить знания детей о модуле числа; План урока1. Общие понятия и определение модуля числа. Общие понятия о модуле числаМодулем числа принято называть само число, если оно не имеет отрицательного значения, или это же число отрицательное, но с противоположным знаком. То есть, модулем неотрицательного действительного числа a является само это число: |а| = а А, модулем отрицательного действительного числа х будет противоположное число: |а| = - а В записи это будет выглядеть так: Для более доступного понимания приведем пример. Так, например, модулем числа 3 будет 3, и также модулем числа -3, является 3. Из этого следует, что под модулем числа подразумевается абсолютная величина, то есть, ее абсолютное значение, но без учета его знака. Если говорить еще более просто, то необходимо от числа отбросить знак. Обозначаться и выглядеть модуль числа может так: |3|, |х|, |а| и т.д. Так, например, модуль числа 3 обозначается |3|. Также, следует помнить, что модуль числа никогда не бывает отрицательным: |a|≥ 0. |5| = 5, |-6| = 6, |-12,45| = 12,45 и т.д. Геометрический смысл модуляМодулем числа называют расстояние, которое измеряется в единичных отрезках от начала координат до точки. В этом определении раскрывается модуль с геометрической точки зрения. Возьмем координатную прямую и обозначим на ней две точки. Пускай этим точкам будут соответствовать такие числа, как −4 и 2. Теперь давайте обратим внимание на данный рисунок. Мы видим, что обозначенная на координатной прямой точка А соответствует числу -4 и если вы внимательно посмотрите, то увидите, что эта точка находится от точки отсчета 0 на расстоянии 4 единичных отрезков. Отсюда следует, что длина отрезка OA равняется четырем единицам. В этом случае, длина отрезка ОА, то есть число 4 будет модулем числа -4. Обозначается и записывается в данном случае модуль числа таким образом: |−4| = 4. Читать эти символы следует таким образом: модуль числа минус четыре равен четырём. Теперь возьмем, и на координатной прямой обозначим точку В. Эта точка В будет соответствовать числу +2, и находится она, как мы видим, от начала отсчета на расстоянии двух единичных отрезков. Из этого следует, что длина отрезка OB равняется двум единицам. В этом случае число 2 будет модулем числа +2. В записи это будет выглядеть так: |+2| = 2 или |2| = 2. А теперь подведем итог. Если мы с вами возьмем какое-то неизвестное число а и обозначим его на координатной прямой точкой А, то в этом случае расстояние от точки A до начала отсчёта, то есть длинна отрезка ОА, как раз и является модулем числа «a». В записи это будет выглядеть так: |a| = OA. Модуль числа его свойстваА теперь давайте попробуем выделить свойства модуля, рассмотреть всевозможные случаи и записать их с помощью буквенных выражений: • Во-первых, модулем числа является число неотрицательное, а значит модуль положительного числа, равен самому числу: |a| = a, если a > 0; • Во-вторых, модули, которые состоят из противоположных чисел, равны: |а| = |–а|. То есть это свойство говорит нам о том, что противоположные числа всегда имеют равные модули, та как на координатной прямой, хотя они и имеют противоположные числа, но они находятся на одинаковом расстоянии от точки отсчета. Из этого следует, что и модули этих противоположных чисел равны. • В-третьих, модуль нуля равняется нулю в том случае, если это число является нулем: |0| = 0, если a = 0. Здесь можно с уверенностью сказать, что модулем нуля является ноль по определению, так как ему соответствует начало отсчета координатной прямой. • Четвертым свойством модуля является то, что модуль произведения двух чисел равен произведению модулей этих чисел. Теперь подробнее рассмотрим, что это значит. Если следовать определению, то мы с вами знаем, что модуль произведения чисел a и b будет равен a•b, или −(a•b), если, а•в ≥ 0, или же – (а•в), если, а•в больше 0. В записи это будет выглядеть так: |а • b| = |а| • |b|. • Пятым свойством является то, что модуль частного от деления чисел равен отношению модулей этих чисел: |а : b| = |а| : |b|. И следующие свойства модуля числа: Решение уравнений и неравенств, которые содержат модуль числаПриступив к решению задач, которые имеют модуль числа, следует помнить, что чтобы решить такое задание, необходимо раскрыть знак модуля, используя знания свойств, которым эта задача соответствует. Задание 1 Так, к примеру, если под знаком модуля стоит выражение, которое зависит от переменной, то раскрывать модуль следует в соответствии с определением: Конечно же, при решении задач бывают случаи, когда модуль раскрывается однозначно. Если, например, взять Или, же для примера берем Задание 2 Перед вами изображена координатная прямая. На этой прямой необходимо отметить числа, модуль которых будет равен 2. Решение В первую очередь, мы должны начертить координатную прямую. Вам уже известно, что для этого, вначале на прямой необходимо выбрать начало отсчета, направление и единичный отрезок. Далее, нам нужно от начала отсчета поставить точки, которые равны расстоянию двух единичных отрезков. Как видим, таких точек на координатной прямой две, одна из которых соответствует числу -2, а другая числу 2. Историческая справка о модуле числаТермин «модуль» произошел от латинского названия modulus, что в переводе обозначает слово «мера». Ввел в обращение этот термин английский математик Роджер Котес. А вот знак модуля был введен благодаря немецкому математику Карлу Вейерштрассу. При написании модуль обозначается с помощью такого символа: | |. Вопросы на закрепление знаний материалаНа сегодняшнем уроке мы с вами познакомились с таким понятием, как модуль числа, а теперь давайте проверим, как вы усвоили эту тему, ответив на поставленные вопросы: 1. Как называется число, которое противоположно положительному числу? Домашнее задание1. Перед вами изображены числа, которые вам нужно расположить в порядке убывания модулей. Если вы правильно выполните задание, то узнаете фамилию человека, который впервые ввел в математику термин «модуль». 2. Начертите координатную прямую и найдите расстояние от М(-5) и К (8) до начала отсчета. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний - Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов -
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: