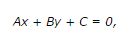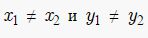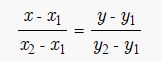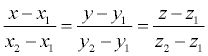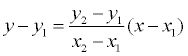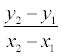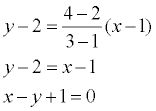|
|
|
| (9 промежуточных версий не показаны.) | | Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Уравнение прямой</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Уравнение прямой, прямая, отрезки, координаты</metakeywords> |
| | | | |
| - | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика: Уравнение прямой'' | + | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика: Уравнение прямой''' |
| | | | |
| - | <br> | + | <h2>Свойства прямой </h2> |
| | | | |
| - | ''' УРАВНЕНИЕ ПРЯМОЙ'''
| + | Вы уже изучали тему о прямой и знаете, что через какую-либо точку можно проводить бесконечное множество прямых. |
| | | | |
| - | <br>Докажем, что любая прямая в декартовых координатах х, у имеет уравнение вида<br>ах + bу+с=0, (*)<br>где а,b, с — некоторые числа, причем хотя бы одно из чисел а, b не равно нулю.
| + | Но если точки не совпадают, то через них можно проводить только одну прямую. |
| | | | |
| - | Пусть h — произвольная прямая на плоскости ху. Проведем какую-нибудь прямую, перпендикулярную прямой h и отложим на ней от точки пересечения С с прямой h равные отрезки СА<sub>1</sub> и CA<sub>2</sub> (рис. 176).
| + | Если же мы имеем две несовпадающие прямые, которые лежат на плоскости, то из предыдущего определения следует, что они либо пересекаются в одной точке, либо же являются параллельными. |
| | | | |
| | + | Если же рассматривать расположение 2-х прямых в трехмерном пространстве, то здесь существует три варианта: |
| | + | |
| | + | • Первый, когда прямые пересекаются;<br> |
| | + | • Второй, когда они параллельны;<br> |
| | + | • Третий, когда прямые скрещиваются.<br> |
| | + | |
| | + | Также стоит вспомнить, что прямая линия в декартовой системе координат, как правило, задается на плоскости уравнением 1-степени, то есть линейным уравнением. |
| | + | |
| | + | <h2>Общее уравнение прямой на плоскости</h2> |
| | + | |
| | + | А теперь пришло время познакомиться с общим уравнением прямой, так как в геометрии нам придется иметь дело именно с ним. |
| | + | |
| | + | Поэтому следует знать следующее определение, в котором говориться, что любая прямая, которая есть на плоскости может быть задана уравнением первого порядка. |
| | + | |
| | + | Это общее уравнение прямой представлено нам в таком виде: |
| | + | <br> |
| | + | [[Image:8kl_Yravnenie01.jpg|200x200px|уравнен.прям]] |
| | <br> | | <br> |
| | + | в котором А,В,С – некоторые числа |
| | | | |
| - | [[Image:22-06-108.jpg]]
| + | Но здесь следует запомнить, что такие постоянные коэффициенты А и В единовременно не могут равняться нулю, поскольку такое уравнение потеряет всякий смысл. |
| | | | |
| - | <br>Пусть a<sub>1</sub>, b<sub>1</sub> — координаты точки А<sub>1</sub> и a<sub>2</sub>, b<sub>2</sub> — координаты точки А<sub>2</sub> Как мы знаем, любая точка А (х; у) прямой h равноудалена от точек А<sub>1</sub> и А<sub>2</sub>. Поэтому координаты ее удовлетворяют уравнению<br>(x-a<sub>1</sub>)<sup>2</sup> + (y-b<sub>1</sub>)<sup>2</sup> =(x-a<sub>2</sub>)<sup>2</sup> + (y-b<sub>2</sub>)<sup>2</sup> ( **)
| + | Теперь мы с вами выяснили, что приведенное выше уравнение первого порядка, как раз и является общим уравнением прямой. |
| | | | |
| - | Обратно: если координаты х и у какой-нибудь точки удовлетворяют уравнению (**), то эта точка равноудалена от точек A<sub>1</sub> и А<sub>2</sub>, а значит, принадлежит прямой h. Таким образом, уравнение (**) является уравнением прямой h. Если в этом уравнении раскрыть скобки и перенести все члены уравнения в левую его часть, то оно примет вид:
| + | А вот в зависимости от значений постоянных А, В и С мы с вами рассмотрим возможные частные варианты: |
| | | | |
| - | [[Image:22-06-109.jpg]] | + | <br> |
| | + | [[Image:8kl_Yravnenie02.jpg|500x500px|уравнен.прям]] |
| | + | <br> |
| | + | <br> |
| | + | [[Image:8kl_Yravnenie03.jpg|500x500px|уравнен.прям]] |
| | + | <br> |
| | + | |
| | + | <h2>Уравнение прямой, проходящей через две точки</h2> |
| | | | |
| - | получаем уравнение (*). По крайней мере одно из чисел a, b не равно нулю, так как точки А<sub>1</sub> и А<sub>2</sub> различны. Утверждение доказано.
| + | Припустим у нас имеются 2 точки А(x1, y1) и В (x2, y2) и через них проходит прямая. Но следует отметить, что точки: |
| | | | |
| - | Задача (35). Составьте уравнение прямой, которая проходит через точки А( — 1; 1), В(1; 0).
| + | <br> |
| | + | [[Image:8kl_Yravnenie04.jpg|200x200px|уравнен.прям]] |
| | + | <br> |
| | + | |
| | + | То в таком случае уравнение можно найти, если использовать следующую формулу: |
| | | | |
| - | Решение. Как мы знаем, наша прямая имеет уравнение вида ах + Ьу + с=0. Точки А и В лежат на прямой, а значит, их координаты удовлетворяют этому уравнению.
| + | <br> |
| | + | [[Image:8kl_Yravnenie05.jpg|200x200px|уравнен.прям]] |
| | + | <br> |
| | | | |
| - | Подставляя координаты точек А и В в уравнение прямой, получим:<br>—а + Ь + с=0, а + с=0.<br>Из этих уравнений можно выразить два коэффициента, например о и Ь, через третий: а = — с, b = —2с. Подставляя эти значения с и b в уравнение прямой, получим:<br>— сх — 2су + с=0.<br><br>На с можно сократить. Тогда получим:
| + | <h2>Уравнение прямой в пространстве</h2> |
| | | | |
| - | -х-2у + 1=0.
| + | Теперь давайте представим, что нам дана прямая, проходящая через точки А(х1, у1, z1) и В (х2, у2, z2), тогда, в этом случае уравнение прямой, проходящей через эти точки будет иметь такой вид: |
| | | | |
| - | Это и есть уравнение нашей прямой.<br><br>
| + | <br> |
| | + | [[Image:8kl_Yravnenie06.jpg|200x200px|уравнен.прям]] |
| | + | <br> |
| | | | |
| - | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br>
| + | Здесь стоит акцентировать внимание на то, что когда какой-то из этих знаменателей будет равен нулю, то необходимо и соответствующий числитель также приравнять к нулю. |
| | | | |
| - | <sub>Полный перечень тем по классам, календарный план согласно школьной программе по математике [[Гипермаркет знаний - первый в мире!|онлайн]], видеоматериал по математике для 8 класса [[Математика|скачать]]</sub>
| + | Теперь давайте запишем это уравнение в упрощенном виде и смотрим, какой вид оно приобрело: |
| | | | |
| | + | <br> |
| | + | [[Image:8kl_Yravnenie07.jpg|200x200px|уравнен.прям]] |
| | + | <br> |
| | + | |
| | + | В случае, если x1≠x2 и x = x1, если x1=x2. |
| | + | |
| | + | Даная дробь, которая имеет вид: |
| | + | |
| | + | <br> |
| | + | [[Image:8kl_Yravnenie008.jpg|100x200px|уравнен.прям]] |
| | <br> | | <br> |
| | | | |
| - | '''<u>Содержание урока</u>'''
| + | будет равна = k и является угловым коэффициентом прямой. |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока '''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас
| + | Пример. |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы
| + | Теперь давайте более подробно рассмотрим на конкретном примере. |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии
| + | |
| - |
| + | Припустим, нам нужно найти уравнение прямой, проходящей через такие точки А(1,2) и В (3,4). |
| - | '''<u>Практика</u>'''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения
| + | Решение. Если мы с вами к этим данным применим формулу, которую мы рассматривали выше, то у нас получится такой результат: |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты
| + | <br> |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания
| + | [[Image:8kl_Yravnenie09.jpg|200x200px|уравнен.прям]] |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы
| + | <br> |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников
| + | |
| | | | |
| - | '''<u>Иллюстрации</u>'''
| + | <h2>Решение задач</h2> |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа '''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты
| + | |
| - |
| + | |
| - | '''<u>Дополнения</u>'''
| + | |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты'''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие
| + | |
| - | '''<u></u>'''
| + | |
| - | <u>Совершенствование учебников и уроков
| + | |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике'''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми
| + | |
| - |
| + | |
| - | '''<u>Только для учителей</u>'''
| + | |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки '''
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы
| + | |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения
| + | |
| - |
| + | |
| - |
| + | |
| - | '''<u>Интегрированные уроки</u>'''<u>
| + | |
| - | </u>
| + | |
| | | | |
| - | <br>
| + | Нам даны точки А (-1, 1) и В (1, 0). Нужно составить уравнение прямой, проходящей через данные точки. |
| | + | |
| | + | Решение. Нам уже известно, что для данной прямой имеет место уравнение такого вида, как ax + by + c = 0. А так как нам известно, что точки А и В лежат на прямой, то отсюда следует вывод, что координаты этих точек соответствуют для решения этого уравнения. |
| | + | |
| | + | Поэтому мы берем и подставляем в это уравнение координаты данных точек и в итоге получаем: |
| | + | |
| | + | -a+ b+ c = 0, a + c = 0. |
| | + | |
| | + | Следуя результатам уравнения, появляется возможность выразить два коэффициента через третий. Например, а и b через а = -c, а b = -2c. Теперь возьмем и подставим эти значения а и b в уравнение прямой. Смотрим, что у нас получилось: |
| | + | |
| | + | - cx– 2cy + c = 0 |
| | | | |
| - | Если у вас есть исправления или предложения к данному уроку, [http://xvatit.com/index.php?do=feedback напишите нам].
| + | Мы видим, что данное уравнение можно сократить, и в результате получаем уравнение нашей прямой, которое будет выглядеть так: |
| | | | |
| - | Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - [http://xvatit.com/forum/ Образовательный форум].
| + | -x – 2y + 1 = 0 |
Текущая версия на 15:57, 2 сентября 2015
Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика: Уравнение прямой
Свойства прямой
Вы уже изучали тему о прямой и знаете, что через какую-либо точку можно проводить бесконечное множество прямых.
Но если точки не совпадают, то через них можно проводить только одну прямую.
Если же мы имеем две несовпадающие прямые, которые лежат на плоскости, то из предыдущего определения следует, что они либо пересекаются в одной точке, либо же являются параллельными.
Если же рассматривать расположение 2-х прямых в трехмерном пространстве, то здесь существует три варианта:
• Первый, когда прямые пересекаются;
• Второй, когда они параллельны;
• Третий, когда прямые скрещиваются.
Также стоит вспомнить, что прямая линия в декартовой системе координат, как правило, задается на плоскости уравнением 1-степени, то есть линейным уравнением.
Общее уравнение прямой на плоскости
А теперь пришло время познакомиться с общим уравнением прямой, так как в геометрии нам придется иметь дело именно с ним.
Поэтому следует знать следующее определение, в котором говориться, что любая прямая, которая есть на плоскости может быть задана уравнением первого порядка.
Это общее уравнение прямой представлено нам в таком виде:
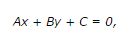
в котором А,В,С – некоторые числа
Но здесь следует запомнить, что такие постоянные коэффициенты А и В единовременно не могут равняться нулю, поскольку такое уравнение потеряет всякий смысл.
Теперь мы с вами выяснили, что приведенное выше уравнение первого порядка, как раз и является общим уравнением прямой.
А вот в зависимости от значений постоянных А, В и С мы с вами рассмотрим возможные частные варианты:


Уравнение прямой, проходящей через две точки
Припустим у нас имеются 2 точки А(x1, y1) и В (x2, y2) и через них проходит прямая. Но следует отметить, что точки:
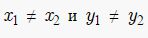
То в таком случае уравнение можно найти, если использовать следующую формулу:
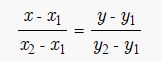
Уравнение прямой в пространстве
Теперь давайте представим, что нам дана прямая, проходящая через точки А(х1, у1, z1) и В (х2, у2, z2), тогда, в этом случае уравнение прямой, проходящей через эти точки будет иметь такой вид:
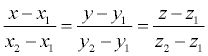
Здесь стоит акцентировать внимание на то, что когда какой-то из этих знаменателей будет равен нулю, то необходимо и соответствующий числитель также приравнять к нулю.
Теперь давайте запишем это уравнение в упрощенном виде и смотрим, какой вид оно приобрело:
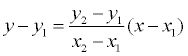
В случае, если x1≠x2 и x = x1, если x1=x2.
Даная дробь, которая имеет вид:
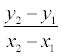
будет равна = k и является угловым коэффициентом прямой.
Пример.
Теперь давайте более подробно рассмотрим на конкретном примере.
Припустим, нам нужно найти уравнение прямой, проходящей через такие точки А(1,2) и В (3,4).
Решение. Если мы с вами к этим данным применим формулу, которую мы рассматривали выше, то у нас получится такой результат:
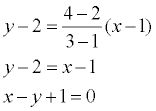
Решение задач
Нам даны точки А (-1, 1) и В (1, 0). Нужно составить уравнение прямой, проходящей через данные точки.
Решение. Нам уже известно, что для данной прямой имеет место уравнение такого вида, как ax + by + c = 0. А так как нам известно, что точки А и В лежат на прямой, то отсюда следует вывод, что координаты этих точек соответствуют для решения этого уравнения.
Поэтому мы берем и подставляем в это уравнение координаты данных точек и в итоге получаем:
-a+ b+ c = 0, a + c = 0.
Следуя результатам уравнения, появляется возможность выразить два коэффициента через третий. Например, а и b через а = -c, а b = -2c. Теперь возьмем и подставим эти значения а и b в уравнение прямой. Смотрим, что у нас получилось:
- cx– 2cy + c = 0
Мы видим, что данное уравнение можно сократить, и в результате получаем уравнение нашей прямой, которое будет выглядеть так:
-x – 2y + 1 = 0
|