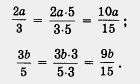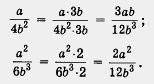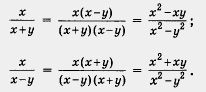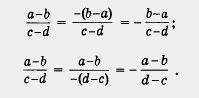|
|
|
| Строка 5: |
Строка 5: |
| | <br> | | <br> |
| | | | |
| | + | <br> |
| | | | |
| - | | + | ''' ОСНОВНОЕ СВОЙСТВО АЛГЕБРАИЧЕСКОЙ ДРОБИ '''<br> |
| - | ''' ОСНОВНОЕ СВОЙСТВО АЛГЕБРАИЧЕСКОЙ ДРОБИ '''<br> | + | |
| | | | |
| | <br>Вам известно, что значение обыкновенной дроби не изменится, если ее числитель и знаменатель одновременно умножить или разделить на одно и то же отличное от нуля число. | | <br>Вам известно, что значение обыкновенной дроби не изменится, если ее числитель и знаменатель одновременно умножить или разделить на одно и то же отличное от нуля число. |
| | | | |
| - | Например: <br> | + | Например: <br> |
| | | | |
| | [[Image:11-06-17.jpg]]<br><br> (и числитель и знаменатель мы одновременно умножили на одно и то же число 4; значение дроби не изменилось); | | [[Image:11-06-17.jpg]]<br><br> (и числитель и знаменатель мы одновременно умножили на одно и то же число 4; значение дроби не изменилось); |
| | | | |
| - | [[Image:11-06-18.jpg]]<br> | + | [[Image:11-06-18.jpg]]<br> |
| | | | |
| | (и числитель и знаменатель мы одно временно разделили на одно и то же число 11; значение дроби не определенном смысле обобщение обыкновенной дро- <br>би; над алгебраическими дробями можно осуществлять преобразования, аналогичные тем, которые мы только что указали для обыкновенных дробей. Эти преобразования можно описать так: | | (и числитель и знаменатель мы одно временно разделили на одно и то же число 11; значение дроби не определенном смысле обобщение обыкновенной дро- <br>би; над алгебраическими дробями можно осуществлять преобразования, аналогичные тем, которые мы только что указали для обыкновенных дробей. Эти преобразования можно описать так: |
| | | | |
| - | ''1. И числитель и знаменатель алгебраической дроби можно умножить на один и тот же многочлен (в частности, на один и тот же одночлен, на одно и то же отличное от нуля число); это — тождественное преобразование заданной алгебраической дроби. <br>'' | + | ''1. И числитель и знаменатель алгебраической дроби можно умножить на один и тот же многочлен (в частности, на один и тот же одночлен, на одно и то же отличное от нуля число); это — тождественное преобразование заданной алгебраической дроби. <br>'' |
| | + | |
| | + | ''2. И числитель и знаменатель алгебраической дроби можно разделить на один и тот же многочлен (в частности, на один и тот же одночлен, на одно и то же отличное от нуля число); это — тождественное преобразование заданной алгебраической дроби, его называют сокращением алгебраической дроби. ''<br> |
| | + | |
| | + | '''Сформулированные правила представляют собой основное свойство алгебраической дроби. '''<br>Пользуясь основным свойством алгебраической дроби, можно дробь —[[Image:11-06-19.jpg]] заменить (если, конечно, в этом есть необходимость) дробью [[Image:11-06-20.jpg]] (числитель и знаменатель одновременно умножили на х - 2) или дробью [[Image:11-06-21.jpg]] (числитель и знаменатель одновременно умножили на 2х). Напротив, пользуясь основным свойством алгебраической дроби, можно заменить дробь [[Image:11-06-21.jpg]] более простой дробью —[[Image:11-06-19.jpg]] (числитель и знаменатель од- <br>новременно разделили на 2х, т. е. сократили дробь). |
| | + | |
| | + | '''Пример'''. Преобразовать заданные дроби так, чтобы получились дроби с одинаковыми знаменателями: |
| | + | |
| | + | [[Image:11-06-22.jpg]] |
| | + | |
| | + | <br>Р е ш е н и е. а) Имеем: |
| | + | |
| | + | [[Image:11-06-23.jpg]]<br><br>Дроби приведены к одинаковому знаменателю (обычно говорят «к общему знаменателю»). Для этого пришлось числитель и знаменатель первой дроби умножить на дополнительный множитель 5, а числитель и знаменатель второй дроби — на дополнительный множитель 3; сделать это позволяет основное свойство дроби. |
| | + | |
| | + | б) Имеем |
| | + | |
| | + | [[Image:11-06-24.jpg]]<br><br>Дроби приведены к общему знаменателю 12b<sup>3</sup> с помощью дополнительных множителей соответственно 3b и 2. <br>в) Имеем |
| | + | |
| | + | [[Image:11-06-25.jpg]]<br><br>Дроби приведены к общему знаменателю х<sup>2</sup> - у<sup>2</sup> с помощью дополнительных множителей соответственно х - у и х + у. |
| | + | |
| | + | Приводя в этом примере алгебраические дроби к общему знаменателю, мы заменяли одну алгебраическую дробь другой дробью, тождественно равной первой. Однако если при сокращении дроби мы ее упрощаем, то в рассмотренном примере каждая дробь заменялась более сложной. Наверное у вас возник вопрос: а нужно ли такое «усложняющее» преобразование? |
| | + | |
| | + | Оказывается, нужно, и в этом мы с вами скоро убедимся. |
| | + | |
| | + | С основным свойством алгебраической дроби связаны правила изменения знаков у числителя и знаменателя. Так, имеет место равенство |
| | + | |
| | + | [[Image:11-06-26.jpg]]<br><br>здесь числитель и знаменатель первой дроби мы одновременно умножили на одно и то же число - 1. |
| | + | |
| | + | Если же изменить знаки только в числителе или только в знаменателе, то следует изменить знак и перед дробью: |
| | | | |
| - | ''2. И числитель и знаменатель алгебраической дроби можно разделить на один и тот же многочлен (в частности, на один и тот же одночлен, на одно и то же отличное от нуля число); это — тождественное преобразование заданной алгебраической дроби, его называют сокращением алгебраической дроби. ''<br>
| + | [[Image:11-06-27.jpg]] |
| | | | |
| - | '''Сформулированные правила представляют собой основное свойство алгебраической дроби. '''<br>Пользуясь основным свойством алгебраической дроби, можно дробь —[[Image:11-06-19.jpg]] заменить (если, конечно, в этом есть необходимость) дробью [[Image:11-06-20.jpg]] (числитель и знаменатель одновременно умножили на х - 2) или дробью [[Image:11-06-21.jpg]] (числитель и знаменатель одновременно умножили на 2х). Напротив, пользуясь основным свойством алгебраической дроби, можно заменить дробь [[Image:11-06-21.jpg]] более простой дробью —г (числитель и знаменатель од- <br>новременно разделили на 2х, т. е. сократили дробь). <br>Пример. Преобразовать заданные дроби так, чтобы по- <br>лучились дроби с одинаковыми знаменателями: <br>2а ЗЪ а а2 х х <br>а) ~а~ и ~с~ > б) 772" И —з" ! В) <br>Р е ш е н и е. а) Имеем: <br>2а _ 2а-5 _ 10а <br>3 ~ ~яЖ ~ 15 <br>и <br>3-5 <br>36 = ЗЬ-3 = 96 <br>5 ~ 5-3 15 ' <br>Дроби приведены к одинаковому знаменателю (обычно гово- <br>рят «к общему знаменателю»). Для этого пришлось числитель и <br>знаменатель первой дроби умножить на дополнительный мно- <br>житель 5, а числитель и знаменатель второй дроби — на допол- <br>нительный множитель 3; сделать это позволяет основное свой- <br>ство дроби. <br>б) Имеем <br>Заб <br>д-ЗЬ <br>а2-2 <br>2а2 <br>1263 <br>Дроби приведены к общему знаменателю 12Ь3 с помощью до- <br>полнительных множителей соответственно ЪЪ и 2. <br>в) Имеем <br>X <br>х+у <br>X <br>Х-У <br>х(х-у) <br>(х+у)(х-у) <br>х(х+у) <br>(х-у)(х+у) <br>х -ху _ <br>х2+ху <br>9 9 • <br>х -у <br>Дроби приведены к общему знаменателю х2 - у2 с помощью <br>дополнительных множителей соответственно х - у и х + у. <¦] <br>Приводя в этом примере алгебраические дроби к общему зна- <br>менателю, мы заменяли одну алгебраическую дробь другой дро- <br>бью, тождественно равной первой. Однако если при сокраще- <br>нии дроби мы ее упрощаем, то в рассмотренном примере каж- <br>дая дробь заменялась более сложной. Наверное у вас возник воп- <br>рос: а нужно ли такое «усложняющее» преобразование? <br>Оказывается, нужно, и в этом мы с вами скоро убедимся. <br>С основным свойством алгебраической дроби связаны прави- <br>ла изменения знаков у числителя и знаменателя. Так, имеет ме- <br>сто равенство <br>а-Ъ Ь-а <br>здесь числитель и знаменатель первой дроби мы одновременно <br>умножили на одно и то же число - 1. <br>Если же изменить знаки только в числителе <br>или только в знаменателе, то следует изменить <br>знак и перед дробью: <br>а-Ь _ -(Ь-а) Ь-а <br>а-Ъ <br>c-d <br>а-Ъ <br>c-d -(d-c) <br>c-d' <br>а-Ъ <br>d-c ' <br>§ 3. СЛОЖЕНИЕ И <br><br><br><br>
| + | <br> |
| | | | |
| - | <br> | + | <br> |
| | | | |
| | <sub>[[Гипермаркет знаний - первый в мире!|онлайн]] библиотека с учебниками и книгами, планы конспектов уроков по математике, задания по математике 8 класса [[Математика|скачать]]</sub> | | <sub>[[Гипермаркет знаний - первый в мире!|онлайн]] библиотека с учебниками и книгами, планы конспектов уроков по математике, задания по математике 8 класса [[Математика|скачать]]</sub> |
Версия 06:20, 11 июня 2010
Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика:Основное свойство алгебраической дроби
ОСНОВНОЕ СВОЙСТВО АЛГЕБРАИЧЕСКОЙ ДРОБИ
Вам известно, что значение обыкновенной дроби не изменится, если ее числитель и знаменатель одновременно умножить или разделить на одно и то же отличное от нуля число.
Например:
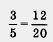
(и числитель и знаменатель мы одновременно умножили на одно и то же число 4; значение дроби не изменилось);
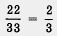
(и числитель и знаменатель мы одно временно разделили на одно и то же число 11; значение дроби не определенном смысле обобщение обыкновенной дро-
би; над алгебраическими дробями можно осуществлять преобразования, аналогичные тем, которые мы только что указали для обыкновенных дробей. Эти преобразования можно описать так:
1. И числитель и знаменатель алгебраической дроби можно умножить на один и тот же многочлен (в частности, на один и тот же одночлен, на одно и то же отличное от нуля число); это — тождественное преобразование заданной алгебраической дроби.
2. И числитель и знаменатель алгебраической дроби можно разделить на один и тот же многочлен (в частности, на один и тот же одночлен, на одно и то же отличное от нуля число); это — тождественное преобразование заданной алгебраической дроби, его называют сокращением алгебраической дроби.
Сформулированные правила представляют собой основное свойство алгебраической дроби.
Пользуясь основным свойством алгебраической дроби, можно дробь —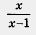 заменить (если, конечно, в этом есть необходимость) дробью заменить (если, конечно, в этом есть необходимость) дробью 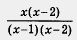 (числитель и знаменатель одновременно умножили на х - 2) или дробью (числитель и знаменатель одновременно умножили на х - 2) или дробью 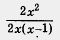 (числитель и знаменатель одновременно умножили на 2х). Напротив, пользуясь основным свойством алгебраической дроби, можно заменить дробь (числитель и знаменатель одновременно умножили на 2х). Напротив, пользуясь основным свойством алгебраической дроби, можно заменить дробь 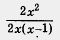 более простой дробью — более простой дробью —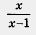 (числитель и знаменатель од- (числитель и знаменатель од-
новременно разделили на 2х, т. е. сократили дробь).
Пример. Преобразовать заданные дроби так, чтобы получились дроби с одинаковыми знаменателями:
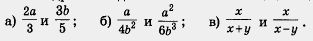
Р е ш е н и е. а) Имеем:
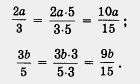
Дроби приведены к одинаковому знаменателю (обычно говорят «к общему знаменателю»). Для этого пришлось числитель и знаменатель первой дроби умножить на дополнительный множитель 5, а числитель и знаменатель второй дроби — на дополнительный множитель 3; сделать это позволяет основное свойство дроби.
б) Имеем
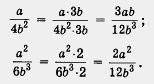
Дроби приведены к общему знаменателю 12b3 с помощью дополнительных множителей соответственно 3b и 2.
в) Имеем
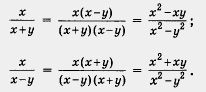
Дроби приведены к общему знаменателю х2 - у2 с помощью дополнительных множителей соответственно х - у и х + у.
Приводя в этом примере алгебраические дроби к общему знаменателю, мы заменяли одну алгебраическую дробь другой дробью, тождественно равной первой. Однако если при сокращении дроби мы ее упрощаем, то в рассмотренном примере каждая дробь заменялась более сложной. Наверное у вас возник вопрос: а нужно ли такое «усложняющее» преобразование?
Оказывается, нужно, и в этом мы с вами скоро убедимся.
С основным свойством алгебраической дроби связаны правила изменения знаков у числителя и знаменателя. Так, имеет место равенство
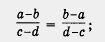
здесь числитель и знаменатель первой дроби мы одновременно умножили на одно и то же число - 1.
Если же изменить знаки только в числителе или только в знаменателе, то следует изменить знак и перед дробью:
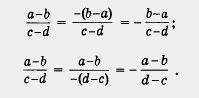
онлайн библиотека с учебниками и книгами, планы конспектов уроков по математике, задания по математике 8 класса скачать
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|