|
|
|
| Строка 7: |
Строка 7: |
| | <br> При счете натуральные числа называют по порядку: <br> 1, 2, 3, 4, 5, 6, 7, 8, 9, ... . | | <br> При счете натуральные числа называют по порядку: <br> 1, 2, 3, 4, 5, 6, 7, 8, 9, ... . |
| | | | |
| - | Из двух натуральных чисел '''меньше''' то, которое при счете называют раньше, и'''больше''' то, которое при счете называют позже. Число 4 меньше, чем 7, а число 8 больше, чем 7. <br> Единица — самое маленькое натуральное число. <br> Точка с меньшей координатой лежит на координатном луче левее точки с большей координатой. <br> Например, точка А(4) лежит левее точки В(7) (рис. 28). <br> Нуль меньше любого натурального числа. | + | Из двух натуральных чисел '''меньше''' то, которое при счете называют раньше, '''больше''' то, которое при счете называют позже. Число 4 меньше, чем 7, а число 8 больше, чем 7. <br> Единица — самое маленькое натуральное число. <br> Точка с меньшей координатой лежит на координатном луче левее точки с большей координатой. <br> Например, точка А(4) лежит левее точки В(7) (рис. 28). <br> Нуль меньше любого натурального числа. |
| | | | |
| | [[Image:15-06-72.jpg]]<br> <br> Результат сравнения двух чисел записывают в виде неравенства, применяя знаки < (меньше) и > (больше). Например, 4 < 7, 8 > 7. Число 3 <br> меньше, чем 6, и больше, чем 2. Это записывают в виде двойного неравенства 2 < 3 < 6. Так как нуль меньше, чем единица, то записывают 0 < 1. | | [[Image:15-06-72.jpg]]<br> <br> Результат сравнения двух чисел записывают в виде неравенства, применяя знаки < (меньше) и > (больше). Например, 4 < 7, 8 > 7. Число 3 <br> меньше, чем 6, и больше, чем 2. Это записывают в виде двойного неравенства 2 < 3 < 6. Так как нуль меньше, чем единица, то записывают 0 < 1. |
| Строка 23: |
Строка 23: |
| | <br> 145. Какая из точек А и В лежит левее на координатном луче: | | <br> 145. Какая из точек А и В лежит левее на координатном луче: |
| | | | |
| - | а) А(1) или В(8); г) А(44) или В(13); <br> б) А(17) или Б(38); д) А(357) или В(375); <br> в) А(1) или В(0); е) А(583) или 5(539)?<br> | + | а) А(1) или В(8); г) А(44) или В(13); <br> б) А(17) или Б(38); д) А(357) или В(375); <br> в) А(1) или В(0); е) А(583) или 5(539)?<br> |
| | | | |
| | 146. Какая из точек С и D лежит правее на координатном луче: | | 146. Какая из точек С и D лежит правее на координатном луче: |
| Строка 29: |
Строка 29: |
| | а) С(3) или D(2); г) С(143) или £>(234); <br> б) С(31) или D(27); д) С(283) или £>(265); <br> в) С(75) или D(57); е) С(1990) или D(1989)? | | а) С(3) или D(2); г) С(143) или £>(234); <br> б) С(31) или D(27); д) С(283) или £>(265); <br> в) С(75) или D(57); е) С(1990) или D(1989)? |
| | | | |
| - | [[Image:15-06-73.jpg]] | + | [[Image:15-06-73.jpg]] |
| | | | |
| | <br> 147. Выясните, какое из двух чисел меньше, и запишите ответ с помощью знака <: <br> а) 1 или 99; г) 7867 или 7876; <br> б) 302 или 299; д) 5 678 000 или 5 675 991; <br> в) 5891 или 654; е) 45 000 823 000 или 45 000 328 001. <br> Прочитайте получившееся | | <br> 147. Выясните, какое из двух чисел меньше, и запишите ответ с помощью знака <: <br> а) 1 или 99; г) 7867 или 7876; <br> б) 302 или 299; д) 5 678 000 или 5 675 991; <br> в) 5891 или 654; е) 45 000 823 000 или 45 000 328 001. <br> Прочитайте получившееся |
| Строка 57: |
Строка 57: |
| | 155. В следующей таблице указан рост учащихся. Назовите их фамилии: | | 155. В следующей таблице указан рост учащихся. Назовите их фамилии: |
| | | | |
| - | а) в порядке возрастания их роста; | + | а) в порядке возрастания их роста; |
| | | | |
| | б) в порядке убывания их роста. | | б) в порядке убывания их роста. |
| Строка 65: |
Строка 65: |
| | 157. Сравните с помощью циркуля отрезки на рис.29 . Назовите эти отрезки в порядке возрастания их длины. | | 157. Сравните с помощью циркуля отрезки на рис.29 . Назовите эти отрезки в порядке возрастания их длины. |
| | | | |
| - | [[Image:15-06-76.jpg]]<br> <br> 158. Точка С лежит между точками А и Б, а точка D — между точками С и В. Какой отрезок длиннее: АВ или CD, AD или AC, CD или СВ? | + | [[Image:15-06-76.jpg]]<br> <br> 158. Точка С лежит между точками А и Б, а точка D — между точками С и В. Какой отрезок длиннее: АВ или CD, AD или AC, CD или СВ? |
| | | | |
| | 159. Вычислите устно: | | 159. Вычислите устно: |
| Строка 75: |
Строка 75: |
| | б) на 8 единичных отрезков. <br> Найдите координаты этих точек. | | б) на 8 единичных отрезков. <br> Найдите координаты этих точек. |
| | | | |
| - | 162. Напишите самое большое и самое маленькое числа среди: <br> а) трехзначных чисел; | + | 162. Напишите самое большое и самое маленькое числа среди: <br> а) трехзначных чисел; |
| | | | |
| | б) пятизначных чисел. | | б) пятизначных чисел. |
| Строка 105: |
Строка 105: |
| | 171. Отметьте на координатном луче все натуральные числа, которые: <br> а) меньше 7; | | 171. Отметьте на координатном луче все натуральные числа, которые: <br> а) меньше 7; |
| | | | |
| - | б) больше 3 и меньше 9; | + | б) больше 3 и меньше 9; |
| | | | |
| | в) больше 9 и меньше 11. | | в) больше 9 и меньше 11. |
| Строка 117: |
Строка 117: |
| | [[Image:15-06-80.jpg]]<br> <br> 175. Верно ли, что: <br> а) 896 - 269 = 227; в) 32 • 55 = 7040; <br> б) 67 • 45 = 2875; г) 1001 : 13 = 100 - 23? | | [[Image:15-06-80.jpg]]<br> <br> 175. Верно ли, что: <br> а) 896 - 269 = 227; в) 32 • 55 = 7040; <br> б) 67 • 45 = 2875; г) 1001 : 13 = 100 - 23? |
| | | | |
| - | 176. Почтовый голубь должен доставить донесение на расстояние 130 км. Скорость голубя 50 км/ч. Успеет ли голубь доставить это донесение: <br> а) за 2 ч; | + | 176. Почтовый голубь должен доставить донесение на расстояние 130 км. Скорость голубя 50 км/ч. Успеет ли голубь доставить это донесение: <br> а) за 2 ч; |
| | | | |
| | б) за 3 ч? | | б) за 3 ч? |
| Строка 123: |
Строка 123: |
| | 177. От Харькова до Севастополя по железной дороге 781 км, а от Харькова до Москвы на 20 км больше. Найдите длину пути по железной дороге от Севастополя до Москвы через Харьков. | | 177. От Харькова до Севастополя по железной дороге 781 км, а от Харькова до Москвы на 20 км больше. Найдите длину пути по железной дороге от Севастополя до Москвы через Харьков. |
| | | | |
| - | [[Image:15-06-81.jpg]] | + | [[Image:15-06-81.jpg]] |
| | | | |
| | <br> 178., Андрей ехал на автомашине из станицы в город со скоростью 55 км/ч. На всю дорогу он потратил 2 ч. Из города в станицу он ехал по той же дороге, но на мопеде со скоростью 22 км/ч. За сколько времени Андрей доедет до станицы? | | <br> 178., Андрей ехал на автомашине из станицы в город со скоростью 55 км/ч. На всю дорогу он потратил 2 ч. Из города в станицу он ехал по той же дороге, но на мопеде со скоростью 22 км/ч. За сколько времени Андрей доедет до станицы? |
| Строка 133: |
Строка 133: |
| | 181. Решите кроссворд, помещенный на форзаце в конце учебника. | | 181. Решите кроссворд, помещенный на форзаце в конце учебника. |
| | | | |
| - | [[Image:15-06-82.jpg]] | + | [[Image:15-06-82.jpg]] |
| | | | |
| | Немало различных способов записи чисел было создано людьми, в Древней Руси числа обозначали буквами с особым знаком ~ (титло), который писали над буквой. <br> Первые девять букв алфавита обозначали единицы, следующие девять букв — десятки, а последние девять букв — сотни. Число десять тысяч называли словом «тьма» (и теперь мы говорим «народу — тьма тьмущая»). | | Немало различных способов записи чисел было создано людьми, в Древней Руси числа обозначали буквами с особым знаком ~ (титло), который писали над буквой. <br> Первые девять букв алфавита обозначали единицы, следующие девять букв — десятки, а последние девять букв — сотни. Число десять тысяч называли словом «тьма» (и теперь мы говорим «народу — тьма тьмущая»). |
| Строка 141: |
Строка 141: |
| | Русские названия чисел тесно связаны с десятичной системой счисления, например, семнадцать означает «семь на десять», семьдесят — «семь десятков», а семьсот — «семь сотен». | | Русские названия чисел тесно связаны с десятичной системой счисления, например, семнадцать означает «семь на десять», семьдесят — «семь десятков», а семьсот — «семь сотен». |
| | | | |
| - | До сих пор используются и римские цифры, которые употреблялись в Древнем Риме уже около 2500 лет тому назад. <br> I — 1, V — 5, X — 10, L — 50, С — 100, D — 500, М — 1000. <br> Остальные числа записываются этими цифрами с применением сложения и вычитания. Так, например, число XXVI! означает 27, так как | + | До сих пор используются и римские цифры, которые употреблялись в Древнем Риме уже около 2500 лет тому назад. <br> I — 1, V — 5, X — 10, L — 50, С — 100, D — 500, М — 1000. <br> Остальные числа записываются этими цифрами с применением сложения и вычитания. Так, например, число XXVI! означает 27, так как |
| | | | |
| | 10 + 10 + 5 + 1 + 1 = 27. | | 10 + 10 + 5 + 1 + 1 = 27. |
| | | | |
| | + | <br> |
| | | | |
| - | | + | [[Image:15-06-83.jpg]] |
| - | [[Image:15-06-83.jpg]] | + | |
| | | | |
| | <br> Если меньшая по значению цифра (I, х, С) стоит перед большей, то ее значение вычитается. Например, IV означает 4 (5 - 1 = 4), IX означает 9 (10 - 1 = 9), ХС означает 90. Таким образом, число mcmlxxxix означает 1989, так как 1000 + (1000 - 100) + 50 + 10 + 10 + 10 + (10 - 1) = 1989. | | <br> Если меньшая по значению цифра (I, х, С) стоит перед большей, то ее значение вычитается. Например, IV означает 4 (5 - 1 = 4), IX означает 9 (10 - 1 = 9), ХС означает 90. Таким образом, число mcmlxxxix означает 1989, так как 1000 + (1000 - 100) + 50 + 10 + 10 + 10 + (10 - 1) = 1989. |
Версия 11:40, 15 июня 2010
Гипермаркет знаний>>Математика>>Математика 5 класс>>Математика:Меньше или больше
Меньше или больше
При счете натуральные числа называют по порядку:
1, 2, 3, 4, 5, 6, 7, 8, 9, ... .
Из двух натуральных чисел меньше то, которое при счете называют раньше, больше то, которое при счете называют позже. Число 4 меньше, чем 7, а число 8 больше, чем 7.
Единица — самое маленькое натуральное число.
Точка с меньшей координатой лежит на координатном луче левее точки с большей координатой.
Например, точка А(4) лежит левее точки В(7) (рис. 28).
Нуль меньше любого натурального числа.

Результат сравнения двух чисел записывают в виде неравенства, применяя знаки < (меньше) и > (больше). Например, 4 < 7, 8 > 7. Число 3
меньше, чем 6, и больше, чем 2. Это записывают в виде двойного неравенства 2 < 3 < 6. Так как нуль меньше, чем единица, то записывают 0 < 1.
Многозначные числа сравнивают так. Число 2305 больше, чем 984, потому что 2305 — четырехзначное число, а 984 — трехзначное. Числа 2305 и 1178 — четырехзначные, но 2305 > 1178, потому что в первом числе больше тысяч, чем во втором. В четырехзначных числах 2305 и 2186 поровну тысяч, но сотен в первом числе больше, и потому 2305 > 2186.
Знаками < и > обозначают также результат сравнения отрезков. Если отрезок АВ короче отрезка CD, то пишут: АВ < CD.
Если же отрезок АВ длиннее отрезка CD, то пишут: АВ > CD.
Какое из натуральных чисел наименьшее?
Какое число меньше 1?
Какое число больше — двузначное или пятизначное?
Как сравнивают числа с одинаковым количеством знаков?
Есть ли число, большее, чем миллиард миллиардов?
145. Какая из точек А и В лежит левее на координатном луче:
а) А(1) или В(8); г) А(44) или В(13);
б) А(17) или Б(38); д) А(357) или В(375);
в) А(1) или В(0); е) А(583) или 5(539)?
146. Какая из точек С и D лежит правее на координатном луче:
а) С(3) или D(2); г) С(143) или £>(234);
б) С(31) или D(27); д) С(283) или £>(265);
в) С(75) или D(57); е) С(1990) или D(1989)?

147. Выясните, какое из двух чисел меньше, и запишите ответ с помощью знака <:
а) 1 или 99; г) 7867 или 7876;
б) 302 или 299; д) 5 678 000 или 5 675 991;
в) 5891 или 654; е) 45 000 823 000 или 45 000 328 001.
Прочитайте получившееся
148. Выясните, какое из чисел больше, и запишите ответ с помощью знака >:
а) 0 или 18; г) 11 871 или 11 859;
б) 74 или 23; д) 2 613 008 или 2 613 001;
в) 147 или 174; е) 6 756 540 623 или 6 756 540 633.
Прочитайте получившееся неравенство.
149. В числах стерли несколько цифр и вместо них поставили звездочки. Выясните, какое из чисел больше, и запишите ответ с помощью одного из
знаков > или <:
а) 71*** или 75***; б) *3*** или *8*.
150. Прочитайте записи:
а) 17 < 18 < 20;
б) 346 < 358 < 400.
151. Назовите все натуральные числа, которые лежат между:
а) 11 и 19; б) 2089 и 2091.
Есть ли натуральное число между 6077 и 6078?

152. Запишите с помощью двойного неравенства:
а) число 10 больше, чем 5, и меньше, чем 15;
б) число 11 меньше, чем 18, и больше, чем 8;
в) число 21 меньше, чем 28, а число 28 меньше, чем 45.
153. Отметьте на координатном луче все натуральные числа, которые:
а) меньше 9;
б) больше 10, но меньше 14.
154. Я задумал число, оканчивающееся цифрой 5. Оно больше, чем 210, и меньше, чем 220. Какое это число?
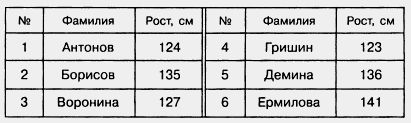
155. В следующей таблице указан рост учащихся. Назовите их фамилии:
а) в порядке возрастания их роста;
б) в порядке убывания их роста.
156. Верно ли, что:
а) 341 + 569 = 910;
б) 25 • 42 = 10 500;
в) 192 : 32 = 38 - 32;
г) 98 • 57 = 23 790 : 78;
д) 23 • 27 < 630;
е) 1288 : 56 > 40?
157. Сравните с помощью циркуля отрезки на рис.29 . Назовите эти отрезки в порядке возрастания их длины.
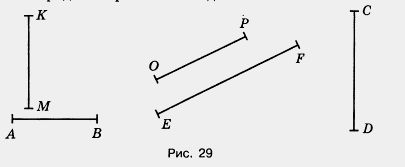
158. Точка С лежит между точками А и Б, а точка D — между точками С и В. Какой отрезок длиннее: АВ или CD, AD или AC, CD или СВ?
159. Вычислите устно:

160. Заполните таблицу:

161. Начертите координатный луч и отметьте на нем точки Л(3); О(0); Б(7); Е(1); С(10). На этом же луче отметьте точки, которые удалены от точки Б:
а) на 2 единичных отрезка;
б) на 8 единичных отрезков.
Найдите координаты этих точек.
162. Напишите самое большое и самое маленькое числа среди:
а) трехзначных чисел;
б) пятизначных чисел.
163. У Андрюши в коллекции 123 почтовые марки, а у Алеши в 3 раза меньше. На сколько марок у Андрюши больше, чем у Алеши?
164. По плану бригада из 13 рабочих должна была изготовить 1248 деталей за 10 ч. Благодаря уменьшению потерь рабочего времени бригада выполнила задание на 2 ч раньше. Сколько деталей изготавливал в час каждый рабочий?
165. Сколькими способами можно прочитать слово «знак» на рисунке? Сравните решение этой задачи с решением задачи

166. Решите задачу:
1) От туристского лагеря до города 84 км. Турист ехал на велосипеде из лагеря в город со скоростью 12 км/ч, а возвращался по той же дороге со скоростью 14 км/ч. На какой путь турист затратил больше времени и на сколько часов?
2) Игорь живет на расстоянии 48 км от районного центра. Путь от дома до районного центра он проехал на велосипеде со скоростью 16 км/ч, а обратный путь по той же дороге он проехал со скоростью 12 км/ч. На какой путь Игорь затратил меньше времени и на сколько часов?
167. Выполните действия:
1) 4428 : 123 - 33; 3) (8032 - 595) : 37;
2) 4000 - 3249 : 57; 4) 10 486 : (2455 - 2357).
168. Какая точка лежит левее на координатном луче:
а) А(58) или В(60); в) Е(3420) или F(3402);
б) С(351) или £(349); г) К(9898) или L(9988)?
169. Какая точка лежит правее на координатном луче:
а) А(37) или 0(0); в) М(8558) или N(8585);
б) С(101) или D(110); г) K(6000) или Р(5999)?
170. Назовите число, оканчивающееся цифрой 3, которое больше, чем 114, и меньше, чем 133.
171. Отметьте на координатном луче все натуральные числа, которые:
а) меньше 7;
б) больше 3 и меньше 9;
в) больше 9 и меньше 11.
172. Сравните числа и поставьте вместо звездочки знак < или знак >:
а) 50 107 * 48 004; г) 30 000 * 29 876;
б) 63 001 * 63 002; д) 2 085 003 * 2 086 003;
в) 41 527 * 41 638; е) 30 000 002 * 30 000 001.
173. Назовите четырехзначное число, которое оканчивается цифрой 1 и которое больше, чем 9981.
174. Какую координату имеет каждая из точек А, Б, С и D, отмеченная на рисунке 30?
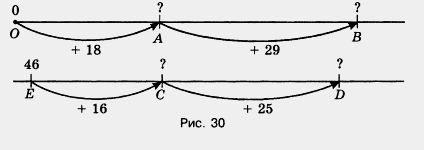
175. Верно ли, что:
а) 896 - 269 = 227; в) 32 • 55 = 7040;
б) 67 • 45 = 2875; г) 1001 : 13 = 100 - 23?
176. Почтовый голубь должен доставить донесение на расстояние 130 км. Скорость голубя 50 км/ч. Успеет ли голубь доставить это донесение:
а) за 2 ч;
б) за 3 ч?
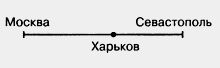
177. От Харькова до Севастополя по железной дороге 781 км, а от Харькова до Москвы на 20 км больше. Найдите длину пути по железной дороге от Севастополя до Москвы через Харьков.
178., Андрей ехал на автомашине из станицы в город со скоростью 55 км/ч. На всю дорогу он потратил 2 ч. Из города в станицу он ехал по той же дороге, но на мопеде со скоростью 22 км/ч. За сколько времени Андрей доедет до станицы?
179. Всадник проехал 80 км за 5 ч. Сколько времени потратит на этот
путь мотоциклист, если его скорость на 24 км/ч больше, чем скорость всад-
ника?
180. Выполните действия:
а) (829 - 239) • 75; в) 3969 : (305 - 158);
б) 2000 - (859 + 1085) : 243; г) 8991 : 111 : 3.
181. Решите кроссворд, помещенный на форзаце в конце учебника.

Немало различных способов записи чисел было создано людьми, в Древней Руси числа обозначали буквами с особым знаком ~ (титло), который писали над буквой.
Первые девять букв алфавита обозначали единицы, следующие девять букв — десятки, а последние девять букв — сотни. Число десять тысяч называли словом «тьма» (и теперь мы говорим «народу — тьма тьмущая»).
Современная достаточно простая и удобная десятичная система записи чисел была заимствована европейцами у арабов, которые в свою очередь переняли
ее у индусов. Поэтому цифры, которыми мы сейчас пользуемся, европейцы называют «арабскими», а арабы — «индийскими». Эта система была введена в Европе примерно в 1120 году английским ученым-путешественником Аделардом. к 1600 году она была принята в большинстве стран мира.
Русские названия чисел тесно связаны с десятичной системой счисления, например, семнадцать означает «семь на десять», семьдесят — «семь десятков», а семьсот — «семь сотен».
До сих пор используются и римские цифры, которые употреблялись в Древнем Риме уже около 2500 лет тому назад.
I — 1, V — 5, X — 10, L — 50, С — 100, D — 500, М — 1000.
Остальные числа записываются этими цифрами с применением сложения и вычитания. Так, например, число XXVI! означает 27, так как
10 + 10 + 5 + 1 + 1 = 27.

Если меньшая по значению цифра (I, х, С) стоит перед большей, то ее значение вычитается. Например, IV означает 4 (5 - 1 = 4), IX означает 9 (10 - 1 = 9), ХС означает 90. Таким образом, число mcmlxxxix означает 1989, так как 1000 + (1000 - 100) + 50 + 10 + 10 + 10 + (10 - 1) = 1989.
В настоящее время римские цифры обычно применяются при нумерации глав и разделов книги, месяцев года, для обозначений дат значительных событий, годовщин.
Для вычислении запись чисел с помощью римских цифр неудобна. В этом вы можете убедиться сами, если попробуете выполнить, например, сложение чисел CCXCVH и XLIX или деление числа CCXCVII на число IX
Н.Я. ВИЛЕНКИН, B. И. ЖОХОВ, А. С. ЧЕСНОКОВ, C. И. ШВАРЦБУРД, Математика 5 класс, Учебник для общеобразовательных учреждений
Математика за 5 класс бесплатно скачать, планы конспектов уроков, готовимся к школе онлайн
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|






















