|
|
|
| Строка 5: |
Строка 5: |
| | <br> | | <br> |
| | | | |
| - | '''РАССТОЯНИЕ МЕЖДУ ТОЧКАМИ''' | + | '''РАССТОЯНИЕ МЕЖДУ ТОЧКАМИ''' |
| | | | |
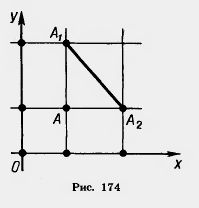
| - | <br>Пусть на плоскости ху даны две точки: А<sub>1</sub> с координатами x<sub>1</sub>, у1 к А<sub>2</sub> с координатами x<sub>2</sub>, у<sub>2</sub>. Выразим расстояние между точками A<sub>1</sub> и А<sub>2</sub> через координаты этих точек.<br> <br>Рассмотрим сначала случай, когда Х1фХ2 и у\фу2- Проведем через точки А, и А2 прямые, параллельные осям координат, и обозначим через А точку их пересечения (рис. 174). Расстояние между точками А и At равно \y\ — yi\, а расстояние между точками А и А2 равно \х,—Х2\. Применяя к прямоугольному треугольнику А А, А 2 теорему Пифагора, получим:<br>d- = {x,—x;f + {y, — ynf, (*)<br>где d — расстояние между точка-<br>ми А, и А. 2. Рис. 174<br>Хотя формула (*) для расстояния между точками выведена нами в предположении Х\фХ2,у\фу2, она остается верной и в других случаях. Действительно, если Х\=Х2, у\фу2, то d равно \у\—у2\- Тот же результат дает и формула (*). Аналогично рассматривается случай, когда Х\фХ2, У\=У2, При Х\ = = Х2, У\=У2 ТОЧКИ А\тл А2 совпадают и формула (*) дает d=0.<br>Задача (19). Найдите на оси х точку, равноудаленную от точек (1; 2) и (2; 3).<br>Решение. Пусть {х; 0) — искомая точка. Приравнивая расстояния от нее до данных точек, получим:<br>(^_l)2 + (0_2f = (x-2f + (0-3f. Отсюда находим л: = 4. Значит, искомая точка есть (4; 0).<br> <br> | + | <br>Пусть на плоскости ху даны две точки: А<sub>1</sub> с координатами x<sub>1</sub>, у1 к А<sub>2</sub> с координатами x<sub>2</sub>, у<sub>2</sub>. Выразим расстояние между точками A<sub>1</sub> и А<sub>2</sub> через координаты этих точек.<br> <br>Рассмотрим сначала случай, когда x<sub>1</sub>[[Image:22-06-97.jpg]]x<sub>2</sub> и у<sub>1</sub>[[Image:22-06-97.jpg]]у<sub>2</sub>- Проведем через точки А, и А<sub>2</sub> прямые, параллельные осям координат, и обозначим через А точку их пересечения (рис. 174). Расстояние между точками А и A<sub>1</sub> равно Iy<sub>1</sub> — y<sub>2</sub>I, а расстояние между точками А и А<sub>2</sub> равно Iх<sub>1</sub>—Х<sub>2</sub>I. Применяя к прямоугольному треугольнику А А<sub>1</sub>А <sub>2</sub> теорему Пифагора, получим:<br>d<sub>2</sub> = (x<sub>1</sub>—x<sub>2</sub>)<sup>2</sup> + (y<sub>1</sub> — y<sub>2</sub>)<sup>2</sup><br> |
| | + | |
| | + | где d — расстояние между точками А<sub>1</sub> и А<sub>2</sub>. <br> |
| | + | |
| | + | [[Image:22-06-103.jpg]]<br> |
| | + | |
| | + | <br>Хотя формула (*) для расстояния между точками выведена нами в предположении x<sub>1</sub> [[Image:22-06-97.jpg]]x<sub>2</sub>,у<sub>1</sub>[[Image:22-06-97.jpg]]у<sub>2</sub>, она остается верной и в других случаях. Действительно, если x<sub>1</sub>=x<sub>2</sub>, у<sub>1</sub>[[Image:22-06-97.jpg]]у<sub>2</sub>, то d равно Iу<sub>1</sub>—у<sub>2</sub>I Тот же результат дает и формула (*). Аналогично рассматривается случай, когда x<sub>1</sub>[[Image:22-06-97.jpg]]x<sub>2</sub>, y<sub>1</sub>=y<sub>2</sub>, При x<sub>1</sub> = x<sub>2</sub>, y<sub>1</sub>=y<sub>2</sub> точки А<sub>1</sub> и А<sub>2</sub> совпадают и формула (*) дает d=0. |
| | + | |
| | + | Задача (19). Найдите на оси х точку, равноудаленную от точек (1; 2) и (2; 3). |
| | + | |
| | + | Решение. Пусть (х; 0) — искомая точка. Приравнивая расстояния от нее до данных точек, получим: |
| | + | |
| | + | (x - 1)<sup>2</sup> + (0-2)<sup>2</sup>= (x-2)<sup>2</sup> + (0-3)<sup>2</sup>. Отсюда находим x = 4. Значит, искомая точка есть (4; 0).<br> <br> |
| | | | |
| | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> | | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> |
Версия 13:03, 22 июня 2010
Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика: Расстояние между точками
РАССТОЯНИЕ МЕЖДУ ТОЧКАМИ
Пусть на плоскости ху даны две точки: А1 с координатами x1, у1 к А2 с координатами x2, у2. Выразим расстояние между точками A1 и А2 через координаты этих точек.
Рассмотрим сначала случай, когда x1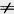 x2 и у1 x2 и у1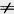 у2- Проведем через точки А, и А2 прямые, параллельные осям координат, и обозначим через А точку их пересечения (рис. 174). Расстояние между точками А и A1 равно Iy1 — y2I, а расстояние между точками А и А2 равно Iх1—Х2I. Применяя к прямоугольному треугольнику А А1А 2 теорему Пифагора, получим: у2- Проведем через точки А, и А2 прямые, параллельные осям координат, и обозначим через А точку их пересечения (рис. 174). Расстояние между точками А и A1 равно Iy1 — y2I, а расстояние между точками А и А2 равно Iх1—Х2I. Применяя к прямоугольному треугольнику А А1А 2 теорему Пифагора, получим:
d2 = (x1—x2)2 + (y1 — y2)2
где d — расстояние между точками А1 и А2.
Хотя формула (*) для расстояния между точками выведена нами в предположении x1 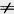 x2,у1 x2,у1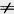 у2, она остается верной и в других случаях. Действительно, если x1=x2, у1 у2, она остается верной и в других случаях. Действительно, если x1=x2, у1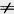 у2, то d равно Iу1—у2I Тот же результат дает и формула (*). Аналогично рассматривается случай, когда x1 у2, то d равно Iу1—у2I Тот же результат дает и формула (*). Аналогично рассматривается случай, когда x1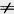 x2, y1=y2, При x1 = x2, y1=y2 точки А1 и А2 совпадают и формула (*) дает d=0. x2, y1=y2, При x1 = x2, y1=y2 точки А1 и А2 совпадают и формула (*) дает d=0.
Задача (19). Найдите на оси х точку, равноудаленную от точек (1; 2) и (2; 3).
Решение. Пусть (х; 0) — искомая точка. Приравнивая расстояния от нее до данных точек, получим:
(x - 1)2 + (0-2)2= (x-2)2 + (0-3)2. Отсюда находим x = 4. Значит, искомая точка есть (4; 0).
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Календарно-тематическое планирование по математике, задачи и ответы школьнику онлайн, курсы учителю по математике скачать
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|











