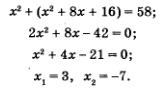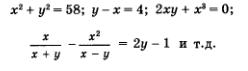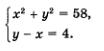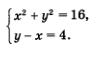|
|
|
| Строка 9: |
Строка 9: |
| | [[Image:Al54.jpg]]<br>Конечно, можно рассматривать рациональные уравнения и с другими переменными, не обязательно с х ну, например, а3 - bx = = 3аb — рациональное уравнение с двумя переменными а, b. Но по традиции в алгебре предпочитают в качестве переменных использовать буквы х, у.<br>'''Определение 2.''' Решением уравнения р (х, у) = 0 называют всякую пару чисел (х;у), которая удовлетворяет этому уравнению, т.е. обращает равенство с переменными р (х, у) = 0 в верное числовое равенство.<br>Например:<br>'''1)''' (3; 7) — решение уравнения х<sup>2</sup> + у<sup>2</sup> = 58. В самом деле, З<sup>2</sup> + 7<sup>2</sup> = 58 — верное числовое равенство.<br>'''2)''' [[Image:Al55.jpg]] — решение уравнения х<sup>2</sup> + у<sup>2</sup> - 58. В самом деле, [[Image:Al56.jpg]] — верное числовое равенство (22 + 36 = 58).<br>'''3)''' (0; 5) — решение уравнения 2ху + х<sup>3</sup> = 0. В самом деле, 2 • 0 • 5 + 0+ О<sup>2</sup> = 0 — верное числовое равенство.<br>'''4)''' (1; 2) не является решением уравнения 2ху + х<sup>3</sup> = 0. В самом деле, 2 • 1 • 2 + 3 = 0 — неверное равенство (получается 5 = 0).<br>Для уравнений с двумя переменными, как и для уравнений с одной переменной, можно ввести понятие равносильности уравнений.<br>Определение 3. Два уравнения р(х, у) = 0 и д(х, у) = 0 называют равносильными, если они имеют одинаковые решения (в частности, если оба уравнения не имеют решений).<br>Обычно при решении уравнения стараются заменить данное уравнение более простым, но равносильным ему. Такую замену называют равносильным преобразованием уравнения. Два основных равносильных преобразования указаны ниже:<br>'''1)''' Перенос членов уравнения из одной части уравнения в другую с противоположными знаками.<br>Например, замена уравнения 2х + bу = 7х - 8у уравнением 2х - 7х — -8у - bу есть равносильное преобразование уравнения.<br>'''2)''' Умножение или деление обеих частей уравнения на одно и то же отличное от нуля число или выражение.<br>Например, замена уравнения 0,5л:2 - 0,3ху = 2у уравнением 5л:2 - 3ху = 20у (обе части уравнения умножили почленно на 10) есть равносильное преобразование уравнения.<br>Неравносильными преобразованиями уравнения, как и в случае уравнений с одной переменной, являются:<br>'''1)''' Освобождение от знаменателей, содержащих переменные.<br>'''2)''' Возведение обеих частей уравнения в квадрат.<br>Если в процессе решения уравнения применялось одно из указанных неравносильных преобразований, то все найденные решения надо проверить подстановкой в исходное уравнение, поскольку среди них могут оказаться посторонние решения.<br>Иногда удается перейти к геометрической (графической) модели уравнения с двумя переменными, т.е. построить график уравнения. Вы, наверное, помните, что графиком линейного уравнения с двумя переменными ах + bу + с = 0 (а, Ь, с — числа, коэффициенты, где хотя бы одно из чисел а, Ь отлично от нуля) является прямая линия — геометрическая модель линейного уравнения. Попробуем найти соответствующие графические модели еще для некоторых рациональных уравнений с двумя переменными х и у.<br>'''Пример 2.''' Построить график уравнения у - 2х2 = 0.<br>'''Решение.''' Преобразуем уравнение к виду у = 2х2. Графиком функции у — 2х2 является парабола, она же считается графиком уравнения у - 2х2 = 0 (рис. 33). <br>'''Пример 3.''' Построить график уравнения ху = 2.<br>'''Решение.''' Преобразуем уравнение к виду [[Image:Al57.jpg]] Графиком функции [[Image:Al58.jpg]] — является гипербола, она же считается графиком уравнения ху = 2 (рис. 34). | | [[Image:Al54.jpg]]<br>Конечно, можно рассматривать рациональные уравнения и с другими переменными, не обязательно с х ну, например, а3 - bx = = 3аb — рациональное уравнение с двумя переменными а, b. Но по традиции в алгебре предпочитают в качестве переменных использовать буквы х, у.<br>'''Определение 2.''' Решением уравнения р (х, у) = 0 называют всякую пару чисел (х;у), которая удовлетворяет этому уравнению, т.е. обращает равенство с переменными р (х, у) = 0 в верное числовое равенство.<br>Например:<br>'''1)''' (3; 7) — решение уравнения х<sup>2</sup> + у<sup>2</sup> = 58. В самом деле, З<sup>2</sup> + 7<sup>2</sup> = 58 — верное числовое равенство.<br>'''2)''' [[Image:Al55.jpg]] — решение уравнения х<sup>2</sup> + у<sup>2</sup> - 58. В самом деле, [[Image:Al56.jpg]] — верное числовое равенство (22 + 36 = 58).<br>'''3)''' (0; 5) — решение уравнения 2ху + х<sup>3</sup> = 0. В самом деле, 2 • 0 • 5 + 0+ О<sup>2</sup> = 0 — верное числовое равенство.<br>'''4)''' (1; 2) не является решением уравнения 2ху + х<sup>3</sup> = 0. В самом деле, 2 • 1 • 2 + 3 = 0 — неверное равенство (получается 5 = 0).<br>Для уравнений с двумя переменными, как и для уравнений с одной переменной, можно ввести понятие равносильности уравнений.<br>Определение 3. Два уравнения р(х, у) = 0 и д(х, у) = 0 называют равносильными, если они имеют одинаковые решения (в частности, если оба уравнения не имеют решений).<br>Обычно при решении уравнения стараются заменить данное уравнение более простым, но равносильным ему. Такую замену называют равносильным преобразованием уравнения. Два основных равносильных преобразования указаны ниже:<br>'''1)''' Перенос членов уравнения из одной части уравнения в другую с противоположными знаками.<br>Например, замена уравнения 2х + bу = 7х - 8у уравнением 2х - 7х — -8у - bу есть равносильное преобразование уравнения.<br>'''2)''' Умножение или деление обеих частей уравнения на одно и то же отличное от нуля число или выражение.<br>Например, замена уравнения 0,5л:2 - 0,3ху = 2у уравнением 5л:2 - 3ху = 20у (обе части уравнения умножили почленно на 10) есть равносильное преобразование уравнения.<br>Неравносильными преобразованиями уравнения, как и в случае уравнений с одной переменной, являются:<br>'''1)''' Освобождение от знаменателей, содержащих переменные.<br>'''2)''' Возведение обеих частей уравнения в квадрат.<br>Если в процессе решения уравнения применялось одно из указанных неравносильных преобразований, то все найденные решения надо проверить подстановкой в исходное уравнение, поскольку среди них могут оказаться посторонние решения.<br>Иногда удается перейти к геометрической (графической) модели уравнения с двумя переменными, т.е. построить график уравнения. Вы, наверное, помните, что графиком линейного уравнения с двумя переменными ах + bу + с = 0 (а, Ь, с — числа, коэффициенты, где хотя бы одно из чисел а, Ь отлично от нуля) является прямая линия — геометрическая модель линейного уравнения. Попробуем найти соответствующие графические модели еще для некоторых рациональных уравнений с двумя переменными х и у.<br>'''Пример 2.''' Построить график уравнения у - 2х2 = 0.<br>'''Решение.''' Преобразуем уравнение к виду у = 2х2. Графиком функции у — 2х2 является парабола, она же считается графиком уравнения у - 2х2 = 0 (рис. 33). <br>'''Пример 3.''' Построить график уравнения ху = 2.<br>'''Решение.''' Преобразуем уравнение к виду [[Image:Al57.jpg]] Графиком функции [[Image:Al58.jpg]] — является гипербола, она же считается графиком уравнения ху = 2 (рис. 34). |
| | | | |
| - | [[Image:Al59.jpg]]Таким образом, если уравнение р(х, у) = О удается преобразовать к виду у = f (x), то график функции у — f (х) считается одновременно и графиком уравнения р(х, у) — 0.<br>'''Пример 4.''' Построить график уравнения х<sup>2</sup> + у<sup>2</sup> = 16.<br>'''Решение.''' Воспользуемся теоремой из курса геометрии: графиком уравнения х<sup>2</sup> + у<sup>2</sup> = г<sup>2</sup>, где r— положительное число, является окружность с центром в начале координат и радиусом r. Значит, графиком уравнения х<sup>2</sup> + у<sup>2</sup> = 16 является окружность с центром в начале координат и радиусом 4 (рис. 35).<br>Упомянутая выше теорема является частным случаем следующей теоремы, которая, надеемся, также известна вам из курса геометрии. | + | [[Image:Al59.jpg]]Таким образом, если уравнение р(х, у) = О удается преобразовать к виду у = f (x), то график функции у — f (х) считается одновременно и графиком уравнения р(х, у) — 0.<br>'''Пример 4.''' Построить график уравнения х<sup>2</sup> + у<sup>2</sup> = 16.<br>'''Решение.''' Воспользуемся теоремой из курса геометрии: графиком уравнения х<sup>2</sup> + у<sup>2</sup> = г<sup>2</sup>, где r— положительное число, является окружность с центром в начале координат и радиусом r. Значит, графиком уравнения х<sup>2</sup> + у<sup>2</sup> = 16 является окружность с центром в начале координат и радиусом 4 (рис. 35).<br>Упомянутая выше теорема является частным случаем следующей теоремы, которая, надеемся, также известна вам из курса геометрии. |
| | | | |
| - | [[Image:al510.jpg]] | + | [[Image:Al510.jpg]] |
| | | | |
| - | [[Image:al511.jpg]]<br>'''Пример 5.''' Построить график уравнения:<br>'''а)''' (х - I)<sup>2</sup> + (у - 2)<sup>2</sup> = 9; '''б) '''х<sup>2</sup> + у<sup>2</sup> + 4х= 0.<br>'''Решение:''' '''а)''' Перепишем уравнение в виде (x - I)<sup>2</sup> + (у - 2)<sup>2</sup> = З2. Графиком этого уравнения, по теореме, является окружность с центром в точке (1; 2) и радиусом 3 (рис. 37).<br>'''б)''' Перепишем уравнение в виде (х<sup>2</sup> + 4х + 4) + у<sup>2</sup> = 4, т.е. (х + 2)<sup>2</sup> + у<sup>2</sup> = 4 и далее (х - (-2))<sup>2</sup> + (у - О)<sup>2</sup> = 22. Графиком этого уравнения, по теореме, является окружность с центром в точке (-2; 0) и радиусом 2 (рис. 38). <br>'''Определение 4.''' Если поставлена задача найти такие пары значений (х; у), которые одновременно удовлетворяют уравнению р (х, у) = 0 и уравнению q (х, у) = 0, то говорят, что указанные уравнения образуют систему уравнений: | + | [[Image:Al511.jpg]]<br>'''Пример 5.''' Построить график уравнения:<br>'''а)''' (х - I)<sup>2</sup> + (у - 2)<sup>2</sup> = 9; '''б) '''х<sup>2</sup> + у<sup>2</sup> + 4х= 0.<br>'''Решение:''' '''а)''' Перепишем уравнение в виде (x - I)<sup>2</sup> + (у - 2)<sup>2</sup> = З2. Графиком этого уравнения, по теореме, является окружность с центром в точке (1; 2) и радиусом 3 (рис. 37).<br>'''б)''' Перепишем уравнение в виде (х<sup>2</sup> + 4х + 4) + у<sup>2</sup> = 4, т.е. (х + 2)<sup>2</sup> + у<sup>2</sup> = 4 и далее (х - (-2))<sup>2</sup> + (у - О)<sup>2</sup> = 22. Графиком этого уравнения, по теореме, является окружность с центром в точке (-2; 0) и радиусом 2 (рис. 38). <br>'''Определение 4.''' Если поставлена задача найти такие пары значений (х; у), которые одновременно удовлетворяют уравнению р (х, у) = 0 и уравнению q (х, у) = 0, то говорят, что указанные уравнения образуют систему уравнений: |
| | | | |
| - | [[Image:al512.jpg]]<br>\р(х,у) = 0, \д(х,у) = 0.<br>система уравнений<br>решение<br>системы<br>уравнений<br>43<br>2.6. I<br>СИСТЕМЫ УРАВНЕНИЙ<br> (*- •1) 2 + [у- 2 У = 1<br> У А <br> <br> <br> У N <br> / \ <br> [ <br> 1 ) <br> \ 0 / ь <br> 2 ч 1 X<br> <br> <br> <br> <br> Ч* к <br> <br> V : + г Г + У ! — ^ <br> <br> / \ <br> ( \ <br> -4 ; 2 0 X<br> \ / <br> <br> <br> <br> <br>Рис. 37<br>Рис. 38<br>Пару значений (х; у), которая одновременно является решением и первого и второго уравнений системы, называют решением системы уравнений. Решить систему уравнений — это значит найти в с е ее решения или установить, что решений нет.<br>Например, пара (3; 7) — решение системы уравнений<br>X2 + у2<br>58,<br>(1)<br>[у - х = 4.<br>В самом деле, эта пара удовлетворяет как первому, так и второму уравнению системы, значит, является ее решением. Обычно пи-<br>{х = 3<br>' —решение системы.<br>У = 7<br>А пара (5; 9) не является решением системы (1): она не удовлетворяет первому уравнению (хотя и удовлетворяет второму уравнению системы).<br>Разумеется, переменные в уравнениях, образующих систему уравнений, могут быть обозначены и другими буквами, например: апЪ, 8тд.1,иъотл. т.д. Но в любом случае при записи ответа в виде<br>44<br>2.6. I<br>СИСТЕМЫ УРАВНЕНИЙ<br>пары чисел используют лексикографический метод, т.е. на первое место ставят ту из двух букв, которая в латинском алфавите встречается раньше.<br>Иногда удается решить систему уравнений графическим методом, с которым вы знакомы: надо построить график первого уравнения, затем построить график второго уравнения и, наконец, найти точки пересечения графиков; координаты каждой точки пересечения служат решением системы уравнений.<br>Пример 6. Решить систему уравнений<br>х2+у2 =16, [у-х = 4.<br>Решение. 1) Построим график уравнения х2+ у2 = 16 — окружность с центром в начале координат и радиусом 4 (рис. 39).<br>2) Построим график уравнения у - х = 4. Это прямая, проходящая через точки (0; 4) и (-4; 0) (рис. 39).<br>3) Окружность и прямая пересекаются в точках А и В (рис. 39). Судя по построенной геометрической модели, точка Л имеет координаты А(-4; 0), а точка В — координаты В(0; 4). Проверка показывает, что на самом деле пара (-4; 0) и пара (0; 4)<br>являются решениями обоих уравнений системы, а значит, и решениями системы уравнений. Следовательно, заданная система уравнений имеет два решения: (-4; 0) и (0; 4).<br>Ответ: (-4; 0); (0; 4).<br>Пример 7. Решить систему уравнений<br>2х2-у = 0, ху — 2.<br>Решение. 1) Переписав первое уравнение системы в виде у = 2х2, приходим к выводу: графиком уравнения является парабола (рис. 40).<br>2) Переписав второе уравнение системы в виде 2<br>у = — , приходим к выводу: графиком уравнения является гипербола (рис. 40).<br>45<br>2.6. I<br>СИСТЕМЫ УРАВНЕНИЙ<br> У< к <br> у- х = 4 <br> 4 В <br> <br> <br> <br>а1/ <br>/г4 0 : I х <br> <br> <br> ~хг <br> + 1 2 16 <br> <br> <br> У' к у- -2> г <br> 1 <br> \ <br> \ <br> \ <br> \ г <br> 11 у -- X <br> \ <br> 0 : 2 X<br> <br> \ <br> <br>Рис. 39 Рис. 40
| + | [[Image:Al512.jpg]][[Image:al513.jpg]]<br> |
| | | | |
| - | 3) Парабола и гипербола пересекаются в точке А (рис. 40). Судя по построенной геометрической модели, точка Л имеет координаты^!.; 2). Проверка показывает, что действительно пара (1; 2) является решением обоих уравнений системы, а значит, и решением системы уравнений. Следовательно, заданная система уравнений имеет одно решение: (1; 2).<br>Ответ: (1; 2).<br>Графический метод решения систем уравнений, как и графический метод решения уравнений, красив, но ненадежен: во-первых, потому, что графики уравнений мы сумеем построить далеко не всегда; во-вторых, даже если графики уравнений удалось построить, точки пересечения могут быть не такими «хорошими», как в специально подобранных примерах 6 и 7, а то и вовсе могут оказаться за пределами чертежа. Значит, нам нужно располагать надежными алгебраическими методами решения систем двух уравнений с двумя переменными. Об этом и пойдет речь в следующем параграфе.<br> (53п <br> ш <br> юратипы <br>внимание <br>46<br>2.6. I<br>СИСТЕМЫ УРАВНЕНИЙ
| + | Пару значений (х; у), которая одновременно является решением и первого и второго уравнений системы, называют решением системы уравнений. Решить систему уравнений — это значит найти все ее решения или установить, что решений нет.<br>Например, пара (3; 7) — решение системы уравнений [[Image:al514.jpg]] |
| | | | |
| - | А.Г. Мордкович Алгебра 9 класс | + | В самом деле, эта пара удовлетворяет как первому, так и второму уравнению системы, значит, является ее решением. Обычно пишут так: (3; 7) - решение системы или [[Image:al515.jpg]] A пара (5; 9) не является решением системы (1): она не удовлетворяет первому уравнению (хотя и удовлетворяет второму уравнению системы).<br>Разумеется, переменные в уравнениях, образующих систему уравнений, могут быть обозначены и другими буквами, например: [[Image:al516.jpg]] Но в любом случае при записи ответа в виде пары чисел используют лексикографический метод, т.е. на первое место ставят ту из двух букв, которая в латинском алфавите встречается раньше.<br>Иногда удается решить систему уравнений графическим методом, с которым вы знакомы: надо построить график первого уравнения, затем построить график второго уравнения и, наконец, найти точки пересечения графиков; координаты каждой точки пересечения служат решением системы уравнений.<br>'''Пример 6.''' Решить систему уравнений [[Image:al517.jpg]]<br>'''Решение. 1)''' Построим график уравнения х<sup>2</sup>+ у<sup>2</sup> = 16 — окружность с центром в начале координат и радиусом 4 (рис. 39).<br>'''2)''' Построим график уравнения у - х = 4. Это прямая, проходящая через точки (0; 4) и (-4; 0) (рис. 39).<br>'''3)''' Окружность и прямая пересекаются в точках А и В (рис. 39). Судя по построенной геометрической модели, точка A имеет координаты А(-4; 0), а точка В — координаты В(0; 4). Проверка показывает, что на самом деле пара (-4; 0) и пара (0; 4) являются решениями обоих уравнений системы, а значит, и решениями системы уравнений. Следовательно, заданная система уравнений имеет два решения: (-4; 0) и (0; 4).<br>'''Ответ:''' (-4; 0); (0; 4).<br>'''Пример 7.''' Решить систему уравнений [[Image:al518.jpg]]<br>'''Решение. 1)''' Переписав первое уравнение системы в виде у = 2х<sup>2</sup>, приходим к выводу: графиком уравнения является парабола (рис. 40).<br>'''2)''' Переписав второе уравнение системы в виде [[Image:al519.jpg]] приходим к выводу: графиком уравнения является гипербола (рис. 40).<br>[[Image:al520.jpg]] |
| | + | |
| | + | '''3)''' Парабола и гипербола пересекаются в точке А (рис. 40). Судя по построенной геометрической модели, точка A имеет координаты A (1; 2). Проверка показывает, что действительно пара (1; 2) является решением обоих уравнений системы, а значит, и решением системы уравнений. Следовательно, заданная система уравнений имеет одно решение: (1; 2).<br>'''Ответ:''' (1; 2).<br>Графический метод решения систем уравнений, как и графический метод решения уравнений, красив, но ненадежен: во-первых, потому, что графики уравнений мы сумеем построить далеко не всегда; во-вторых, даже если графики уравнений удалось построить, точки пересечения могут быть не такими «хорошими», как в специально подобранных примерах 6 и 7, а то и вовсе могут оказаться за пределами чертежа. Значит, нам нужно располагать надежными алгебраическими методами решения систем двух уравнений с двумя переменными. Об этом и пойдет речь в следующем параграфе. |
| | + | |
| | + | <br> А.Г. Мордкович Алгебра 9 класс |
| | | | |
| | <br> | | <br> |
Версия 11:23, 24 июня 2010
Гипермаркет знаний>>Математика>>Математика 9 класс>>Математика: Системы уравнений. Основные понятия
ОСНОВНЫЕ ПОНЯТИЯ
С системами уравнений вы уже встречались в курсе алгебры 7-го класса, но это были только системы специального вида — системы двух линейных уравнений с двумя переменными. В 8-м классе вы научились решать рациональные уравнения с одной переменной, значит, можно подумать и о решении систем рациональных уравнений с двумя переменными, тем более что такие системы довольно часто представляют собой математические модели изучаемых ситуаций. Об одной из таких моделей вы уже узнали из учебника «Алгебра-8». Приведенный ниже пример заимствован из указанного учебника.
Пример 1. Задумано двузначное число. Известно, что: 1) сумма квадратов цифр задуманного числа равна 58; 2) если цифры задуманного числа поменять местами, то получится двузначное число, которое больше задуманного на 36. Какое число задумано?
Решение. Первый этап. Составление математической модели.
Для перевода ситуации с обыденного языка на математический придется ввести не одну, а две переменные: х — цифра десятков, у — цифра единиц задуманного числа. Само задуманное число выражается формулой 10х + у. Если же цифры поменять местами, то получится число 10у + х.
По условию, сумма квадратов цифр задуманного числа равна 58; это значит, что х2 + у2 = 58.
Далее, по условию, если цифры задуманного числа поменять местами, то получится число (оно, как мы отметили выше, выражается формулой 10у + х), которое больше задуманного (т.е. числа 10х + у) на 36. Это значит, что (10у + х) - (10х + у) = 36, откуда после понятных упрощений получим у - х = 4.
Таким образом, математическая модель задачи представляет собой систему уравнений: 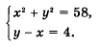
Второй этап. Работа с составленной моделью.
Воспользуемся методом подстановки: выразим у через х из второго уравнения и подставим полученное выражение вместо у в первое уравнение.
1) Из второго уравнения системы выразим у: у — х + 4.
2) Подставим полученное выражение вместо у в первое уравнение системы: х2 + (х + 4)2 = 58.
3) Решим полученное уравнение:
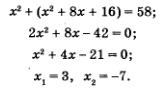
4) Подставим поочередно каждое из найденных значений х в формулу у = х + 4. Если х = 3, то у = 3 + 4 = 7; если х = -7, то у = -7 + 4 = -3.
5) Пары (3; 7) и (-7; -3) — решения заданной системы уравнений.
Третий этап. Ответ на вопрос задачи.
По условию, х и у — цифры двузначного числа. Отрицательными цифры быть не могут, значит, пару (-7; -3) придется отвергнуть как не соответствующую условиям задачи. Остается пара (3; 7), т.е. х = 3, у = 7. Переменные х и у имеют следующий смысл: цифра десятков, а у — цифра единиц задуманного двузначного числа. Значит, было задумано число 37.
От в ет: 37.
Таким образом, определенные представления о системах уравнений у нас есть, нужно их уточнить и продвинуться в изучении теории дальше.
Определение 1. Рациональным уравнением с двумя переменными х, у называют уравнение вида р (х, у) = 0, где р (х, у) — рациональное выражение (т.е. алгебраическое выражение, составленное из чисел и переменных х, у с помощью операций сложения, вычитания, умножения, деления и возведения в натуральную степень).
На практике удобнее более широкое истолкование термина «рациональное уравнение с двумя переменными»: это уравнение вида 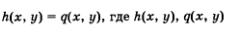 — рациональные выражения с двумя переменными х и у. — рациональные выражения с двумя переменными х и у.
Примеры рациональных уравнений с двумя переменными:
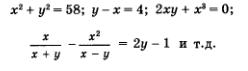
Конечно, можно рассматривать рациональные уравнения и с другими переменными, не обязательно с х ну, например, а3 - bx = = 3аb — рациональное уравнение с двумя переменными а, b. Но по традиции в алгебре предпочитают в качестве переменных использовать буквы х, у.
Определение 2. Решением уравнения р (х, у) = 0 называют всякую пару чисел (х;у), которая удовлетворяет этому уравнению, т.е. обращает равенство с переменными р (х, у) = 0 в верное числовое равенство.
Например:
1) (3; 7) — решение уравнения х2 + у2 = 58. В самом деле, З2 + 72 = 58 — верное числовое равенство.
2) 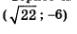 — решение уравнения х2 + у2 - 58. В самом деле, — решение уравнения х2 + у2 - 58. В самом деле, 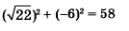 — верное числовое равенство (22 + 36 = 58). — верное числовое равенство (22 + 36 = 58).
3) (0; 5) — решение уравнения 2ху + х3 = 0. В самом деле, 2 • 0 • 5 + 0+ О2 = 0 — верное числовое равенство.
4) (1; 2) не является решением уравнения 2ху + х3 = 0. В самом деле, 2 • 1 • 2 + 3 = 0 — неверное равенство (получается 5 = 0).
Для уравнений с двумя переменными, как и для уравнений с одной переменной, можно ввести понятие равносильности уравнений.
Определение 3. Два уравнения р(х, у) = 0 и д(х, у) = 0 называют равносильными, если они имеют одинаковые решения (в частности, если оба уравнения не имеют решений).
Обычно при решении уравнения стараются заменить данное уравнение более простым, но равносильным ему. Такую замену называют равносильным преобразованием уравнения. Два основных равносильных преобразования указаны ниже:
1) Перенос членов уравнения из одной части уравнения в другую с противоположными знаками.
Например, замена уравнения 2х + bу = 7х - 8у уравнением 2х - 7х — -8у - bу есть равносильное преобразование уравнения.
2) Умножение или деление обеих частей уравнения на одно и то же отличное от нуля число или выражение.
Например, замена уравнения 0,5л:2 - 0,3ху = 2у уравнением 5л:2 - 3ху = 20у (обе части уравнения умножили почленно на 10) есть равносильное преобразование уравнения.
Неравносильными преобразованиями уравнения, как и в случае уравнений с одной переменной, являются:
1) Освобождение от знаменателей, содержащих переменные.
2) Возведение обеих частей уравнения в квадрат.
Если в процессе решения уравнения применялось одно из указанных неравносильных преобразований, то все найденные решения надо проверить подстановкой в исходное уравнение, поскольку среди них могут оказаться посторонние решения.
Иногда удается перейти к геометрической (графической) модели уравнения с двумя переменными, т.е. построить график уравнения. Вы, наверное, помните, что графиком линейного уравнения с двумя переменными ах + bу + с = 0 (а, Ь, с — числа, коэффициенты, где хотя бы одно из чисел а, Ь отлично от нуля) является прямая линия — геометрическая модель линейного уравнения. Попробуем найти соответствующие графические модели еще для некоторых рациональных уравнений с двумя переменными х и у.
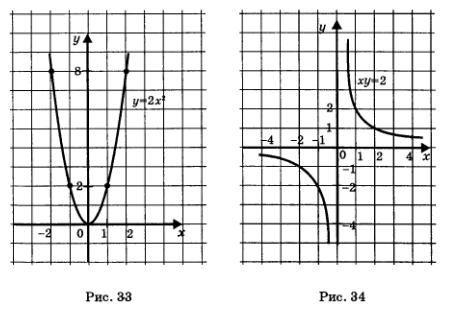
Пример 2. Построить график уравнения у - 2х2 = 0.
Решение. Преобразуем уравнение к виду у = 2х2. Графиком функции у — 2х2 является парабола, она же считается графиком уравнения у - 2х2 = 0 (рис. 33).
Пример 3. Построить график уравнения ху = 2.
Решение. Преобразуем уравнение к виду 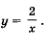 Графиком функции Графиком функции 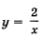 — является гипербола, она же считается графиком уравнения ху = 2 (рис. 34). — является гипербола, она же считается графиком уравнения ху = 2 (рис. 34).
 Таким образом, если уравнение р(х, у) = О удается преобразовать к виду у = f (x), то график функции у — f (х) считается одновременно и графиком уравнения р(х, у) — 0. Таким образом, если уравнение р(х, у) = О удается преобразовать к виду у = f (x), то график функции у — f (х) считается одновременно и графиком уравнения р(х, у) — 0.
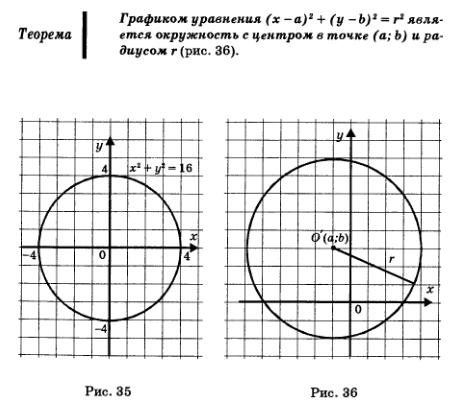
Пример 4. Построить график уравнения х2 + у2 = 16.
Решение. Воспользуемся теоремой из курса геометрии: графиком уравнения х2 + у2 = г2, где r— положительное число, является окружность с центром в начале координат и радиусом r. Значит, графиком уравнения х2 + у2 = 16 является окружность с центром в начале координат и радиусом 4 (рис. 35).
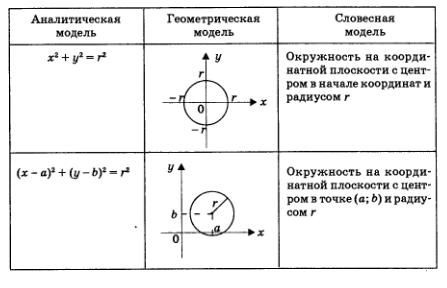
Упомянутая выше теорема является частным случаем следующей теоремы, которая, надеемся, также известна вам из курса геометрии.
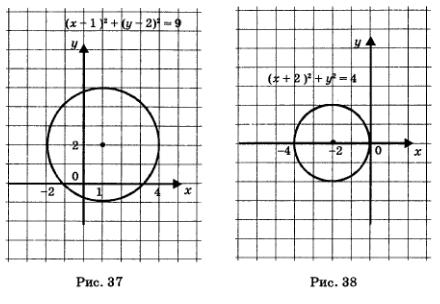
Пример 5. Построить график уравнения:
а) (х - I)2 + (у - 2)2 = 9; б) х2 + у2 + 4х= 0.
Решение: а) Перепишем уравнение в виде (x - I)2 + (у - 2)2 = З2. Графиком этого уравнения, по теореме, является окружность с центром в точке (1; 2) и радиусом 3 (рис. 37).
б) Перепишем уравнение в виде (х2 + 4х + 4) + у2 = 4, т.е. (х + 2)2 + у2 = 4 и далее (х - (-2))2 + (у - О)2 = 22. Графиком этого уравнения, по теореме, является окружность с центром в точке (-2; 0) и радиусом 2 (рис. 38).
Определение 4. Если поставлена задача найти такие пары значений (х; у), которые одновременно удовлетворяют уравнению р (х, у) = 0 и уравнению q (х, у) = 0, то говорят, что указанные уравнения образуют систему уравнений:
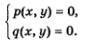 
Пару значений (х; у), которая одновременно является решением и первого и второго уравнений системы, называют решением системы уравнений. Решить систему уравнений — это значит найти все ее решения или установить, что решений нет.
Например, пара (3; 7) — решение системы уравнений 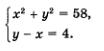
В самом деле, эта пара удовлетворяет как первому, так и второму уравнению системы, значит, является ее решением. Обычно пишут так: (3; 7) - решение системы или Файл:Al515.jpg A пара (5; 9) не является решением системы (1): она не удовлетворяет первому уравнению (хотя и удовлетворяет второму уравнению системы).
Разумеется, переменные в уравнениях, образующих систему уравнений, могут быть обозначены и другими буквами, например: Файл:Al516.jpg Но в любом случае при записи ответа в виде пары чисел используют лексикографический метод, т.е. на первое место ставят ту из двух букв, которая в латинском алфавите встречается раньше.
Иногда удается решить систему уравнений графическим методом, с которым вы знакомы: надо построить график первого уравнения, затем построить график второго уравнения и, наконец, найти точки пересечения графиков; координаты каждой точки пересечения служат решением системы уравнений.
Пример 6. Решить систему уравнений 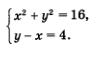
Решение. 1) Построим график уравнения х2+ у2 = 16 — окружность с центром в начале координат и радиусом 4 (рис. 39).
2) Построим график уравнения у - х = 4. Это прямая, проходящая через точки (0; 4) и (-4; 0) (рис. 39).
3) Окружность и прямая пересекаются в точках А и В (рис. 39). Судя по построенной геометрической модели, точка A имеет координаты А(-4; 0), а точка В — координаты В(0; 4). Проверка показывает, что на самом деле пара (-4; 0) и пара (0; 4) являются решениями обоих уравнений системы, а значит, и решениями системы уравнений. Следовательно, заданная система уравнений имеет два решения: (-4; 0) и (0; 4).
Ответ: (-4; 0); (0; 4).
Пример 7. Решить систему уравнений 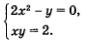
Решение. 1) Переписав первое уравнение системы в виде у = 2х2, приходим к выводу: графиком уравнения является парабола (рис. 40).
2) Переписав второе уравнение системы в виде 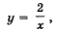 приходим к выводу: графиком уравнения является гипербола (рис. 40). приходим к выводу: графиком уравнения является гипербола (рис. 40).
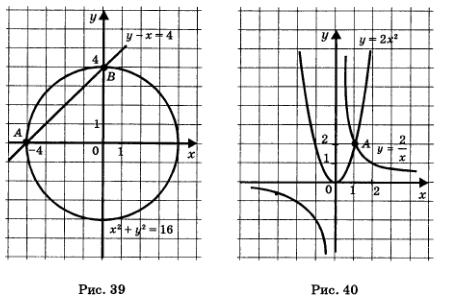
3) Парабола и гипербола пересекаются в точке А (рис. 40). Судя по построенной геометрической модели, точка A имеет координаты A (1; 2). Проверка показывает, что действительно пара (1; 2) является решением обоих уравнений системы, а значит, и решением системы уравнений. Следовательно, заданная система уравнений имеет одно решение: (1; 2).
Ответ: (1; 2).
Графический метод решения систем уравнений, как и графический метод решения уравнений, красив, но ненадежен: во-первых, потому, что графики уравнений мы сумеем построить далеко не всегда; во-вторых, даже если графики уравнений удалось построить, точки пересечения могут быть не такими «хорошими», как в специально подобранных примерах 6 и 7, а то и вовсе могут оказаться за пределами чертежа. Значит, нам нужно располагать надежными алгебраическими методами решения систем двух уравнений с двумя переменными. Об этом и пойдет речь в следующем параграфе.
А.Г. Мордкович Алгебра 9 класс
Материалы по математике онлайн, задачи и ответы по классам, планы конспектов уроков по математике скачать
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|