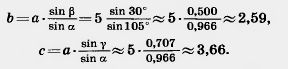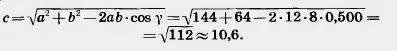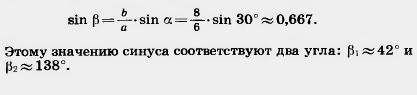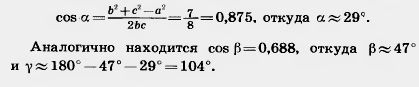|
|
|
| Строка 5: |
Строка 5: |
| | <br> | | <br> |
| | | | |
| - | ''' РЕШЕНИЕ ТРЕУГОЛЬНИКОВ''' | + | ''' РЕШЕНИЕ ТРЕУГОЛЬНИКОВ''' |
| | | | |
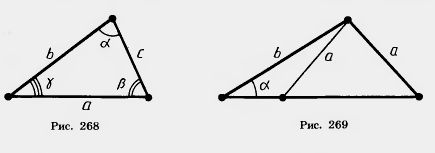
| - | <br>Решение треугольников состоит в нахождении неизвестных сторон и углов треугольника по известным его углам и сторонам. Будем обозначать стороны треугольника через а, b, с, а противолежащие им углы через [[Image:24-06-55.jpg]](рис. 268). | + | <br>Решение треугольников состоит в нахождении неизвестных сторон и углов треугольника по известным его углам и сторонам. Будем обозначать стороны треугольника через а, b, с, а противолежащие им углы через [[Image:24-06-55.jpg]](рис. 268). |
| | | | |
| - | Задача (26). 1) В треугольнике даны сторона а = 5 и два угла [[Image:24-06-53.jpg]] = 30°, [[Image:24-06-56.jpg]] = 45°. Найдите третий угол и остальные две стороны.<br>Решение. Так как сумма углов треугольника равна 180°, то третий угол а выражается через заданные углы:<br>[[Image:24-06-52.jpg]] = 180°-[[Image:24-06-53.jpg]]-[[Image:24-06-56.jpg]] = 180°-30°-45° = 105°.<br>Зная сторону и все три угла, по теореме синусов находим две остальные стороны: | + | Задача (26). 1) В треугольнике даны сторона а = 5 и два угла [[Image:24-06-53.jpg]] = 30°, [[Image:24-06-56.jpg]] = 45°. Найдите третий угол и остальные две стороны.<br>Решение. Так как сумма углов треугольника равна 180°, то третий угол а выражается через заданные углы:<br>[[Image:24-06-52.jpg]] = 180°-[[Image:24-06-53.jpg]]-[[Image:24-06-56.jpg]] = 180°-30°-45° = 105°.<br>Зная сторону и все три угла, по теореме синусов находим две остальные стороны: |
| | | | |
| - | [[Image:24-06-57.jpg]]<br><br>Задача (27). 1) В треугольнике даны две стороны a=12, b = 8 и угол между ними [[Image:24-06-56.jpg]] = 60°. Найдите остальные два угла и третью сторону.<br>Решение. Третью сторону находим по теореме косинусов : | + | [[Image:24-06-57.jpg]]<br><br>Задача (27). 1) В треугольнике даны две стороны a=12, b = 8 и угол между ними [[Image:24-06-56.jpg]] = 60°. Найдите остальные два угла и третью сторону.<br>Решение. Третью сторону находим по теореме косинусов : |
| | | | |
| - | [[Image:24-06-58.jpg]]<br><br>Теперь, имея три стороны, по теореме косинусов находим косинусы двух неизвестных углов и сами углы: | + | [[Image:24-06-58.jpg]]<br><br>Теперь, имея три стороны, по теореме косинусов находим косинусы двух неизвестных углов и сами углы: |
| | | | |
| - | [[Image:24-06-59.jpg]]<br><br>Задача (28). 5) В треугольнике даны две стороны а = 6, b = 8 и противолежащий стороне [[Image:24-06-52.jpg]] угол [[Image:24-06-52.jpg]] = 30°. Найдите остальные два угла и третью сторону.<br>Решение. По теореме синусов находим значение sin [[Image:24-06-53.jpg]]: | + | [[Image:24-06-59.jpg]]<br><br>Задача (28). 5) В треугольнике даны две стороны а = 6, b = 8 и противолежащий стороне [[Image:24-06-52.jpg]] угол [[Image:24-06-52.jpg]] = 30°. Найдите остальные два угла и третью сторону.<br>Решение. По теореме синусов находим значение sin [[Image:24-06-53.jpg]]: |
| | | | |
| - | <br>[[Image:24-06-60.jpg]]<br><br>[[Image:24-06-61.jpg]] | + | <br>[[Image:24-06-60.jpg]]<br><br>[[Image:24-06-61.jpg]] |
| | | | |
| - | <br>Рассмотрим сначала угол [[Image:24-06-62.jpg]] По нему находим третий угол [[Image:24-06-63.jpg]] и по теореме синусов третью сторону | + | <br>Рассмотрим сначала угол [[Image:24-06-62.jpg]] По нему находим третий угол [[Image:24-06-63.jpg]] и по теореме синусов третью сторону |
| | | | |
| - | [[Image:24-06-64.jpg]]<br> | + | [[Image:24-06-64.jpg]]<br> |
| | | | |
| - | [[Image:24-06-65.jpg]]<br><br>Замечание. Мы видим, что эта задача в отличие от предыдущих имеет два решения (рис. 269). При других численных данных, например при [[Image:24-06-52.jpg]][[Image:24-06-66.jpg]] 90°, задача может иметь лишь одно решение или вовсе не иметь решений. | + | [[Image:24-06-65.jpg]]<br><br>Замечание. Мы видим, что эта задача в отличие от предыдущих имеет два решения (рис. 269). При других численных данных, например при [[Image:24-06-52.jpg]][[Image:24-06-66.jpg]] 90°, задача может иметь лишь одно решение или вовсе не иметь решений. |
| | | | |
| - | Задача (29). 1) Даны три стороны треугольника: а = 2, b = 3, с=4. Найдите его углы. | + | Задача (29). 1) Даны три стороны треугольника: а = 2, b = 3, с=4. Найдите его углы. |
| | | | |
| - | Решение. Углы находятся по теореме косинусов: | + | Решение. Углы находятся по теореме косинусов: |
| | | | |
| - | <br>c[[Image:24-06-67.jpg]]<br> | + | <br>[[Image:24-06-67.jpg]]<br> |
| | | | |
| | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> | | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> |
Версия 11:24, 24 июня 2010
Гипермаркет знаний>>Математика>>Математика 9 класс>>Математика:Решение треугольников
РЕШЕНИЕ ТРЕУГОЛЬНИКОВ
Решение треугольников состоит в нахождении неизвестных сторон и углов треугольника по известным его углам и сторонам. Будем обозначать стороны треугольника через а, b, с, а противолежащие им углы через 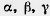 (рис. 268). (рис. 268).
Задача (26). 1) В треугольнике даны сторона а = 5 и два угла  = 30°, = 30°, 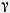 = 45°. Найдите третий угол и остальные две стороны. = 45°. Найдите третий угол и остальные две стороны.
Решение. Так как сумма углов треугольника равна 180°, то третий угол а выражается через заданные углы:
 = 180°- = 180°- - -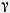 = 180°-30°-45° = 105°. = 180°-30°-45° = 105°.
Зная сторону и все три угла, по теореме синусов находим две остальные стороны:
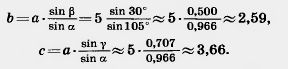
Задача (27). 1) В треугольнике даны две стороны a=12, b = 8 и угол между ними 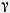 = 60°. Найдите остальные два угла и третью сторону. = 60°. Найдите остальные два угла и третью сторону.
Решение. Третью сторону находим по теореме косинусов :
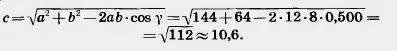
Теперь, имея три стороны, по теореме косинусов находим косинусы двух неизвестных углов и сами углы:

Задача (28). 5) В треугольнике даны две стороны а = 6, b = 8 и противолежащий стороне  угол угол  = 30°. Найдите остальные два угла и третью сторону. = 30°. Найдите остальные два угла и третью сторону.
Решение. По теореме синусов находим значение sin  : :
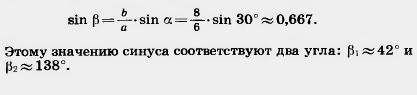
Рассмотрим сначала угол 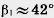 По нему находим третий угол По нему находим третий угол 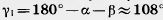 и по теореме синусов третью сторону и по теореме синусов третью сторону

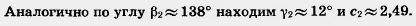
Замечание. Мы видим, что эта задача в отличие от предыдущих имеет два решения (рис. 269). При других численных данных, например при  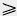 90°, задача может иметь лишь одно решение или вовсе не иметь решений. 90°, задача может иметь лишь одно решение или вовсе не иметь решений.
Задача (29). 1) Даны три стороны треугольника: а = 2, b = 3, с=4. Найдите его углы.
Решение. Углы находятся по теореме косинусов:
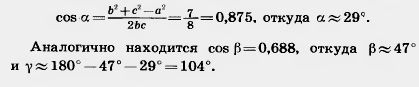
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Книги и учебники согласно календарному плануванння по математике 9 класса скачать, помощь школьнику онлайн
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|