|
|
|
| Строка 5: |
Строка 5: |
| | <br> | | <br> |
| | | | |
| - | '''ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ'''<br> | + | '''ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ'''<br> |
| | | | |
| - | <br>'''''Выпуклый многоугольник называется правильным, если у него все стороны равны и все углы равны.''''' | + | <br>'''''Выпуклый многоугольник называется правильным, если у него все стороны равны и все углы равны.''''' |
| | | | |
| - | Многоугольник называется '''''вписанным в окружность''''', если все его вершины лежат на некоторой окружности. Многоугольник называется '''''описанным около окружности''''', если все его стороны касаются некоторой окружности.<br> | + | Многоугольник называется '''''вписанным в окружность''''', если все его вершины лежат на некоторой окружности. Многоугольник называется '''''описанным около окружности''''', если все его стороны касаются некоторой окружности.<br> |
| | | | |
| - | Теорема 13.3. '''''Правильный выпуклый многоугольник является вписанным в окружность и описанным около окружности.'''''<br> | + | Теорема 13.3. '''''Правильный выпуклый многоугольник является вписанным в окружность и описанным около окружности.'''''<br> |
| | | | |
| - | Доказательство. Пусть А и В — две соседние вершины правильного многоугольника (рис. 280). Проведем биссектрисы углов многоугольника из вершин А и В. Пусть О — точка их пересечения. Треугольник АОВ равнобедренный с основанием АВ и углами при основании, равными [[Image:24-06-76.jpg]] где [[Image:24-06-52.jpg]] —угол многоугольника.<br> | + | Доказательство. Пусть А и В — две соседние вершины правильного многоугольника (рис. 280). Проведем биссектрисы углов многоугольника из вершин А и В. Пусть О — точка их пересечения. Треугольник АОВ равнобедренный с основанием АВ и углами при основании, равными [[Image:24-06-76.jpg]] где [[Image:24-06-52.jpg]] —угол многоугольника.<br> |
| | | | |
| - | Соединим точку О с вершиной С, соседней с В. Треугольники АВО и СВО равны по первому признаку равенства треугольников. У них сторона ОВ общая, стороны АВ и ВС равны как стороны многоугольника, а углы при вершине В равны Из равенства треугольников следует, что треугольник ОВС равнобедренный с углом при вершине С, равным [[Image:24-06-76.jpg]], т. е. СО есть биссектриса угла С.<br>Теперь соединяем точку О с вершиной D, соседней с С, и доказываем, что треугольник COD равнобедренный и DO — биссектриса угла D многоугольника. И т. д.<br> <br>В итоге получается, что каждый треугольник, у которого одна сторона есть сторона многоугольника, а противолежащая вершина — точка О, является равнобедренным. Все эти треугольники имеют равные боковые стороны и равные высоты, опущенные на их основания. Отсюда следует, что все вершины многоугольника находятся на окружности с центром О и радиусом, равным боковым сторонам треугольников, а все стороны многоугольника касаются окружности с центром О и радиусом,<br>равным высотам треугольников, опущенным из вершины О. Теорема доказана.<br>Вписанная и описанная окружности<br>правильного многоугольника имеют<br>один и тот же центр. Его называют<br>центром многоугольника. Угол, под ко-<br>торым видна сторона правильного мно-<br>гоугольника из его центра, называет-<br>ся центральным углом многоуголь-<br>Рис. 280 ника.<br><br><br><br> | + | Соединим точку О с вершиной С, соседней с В. Треугольники АВО и СВО равны по первому признаку равенства треугольников. У них сторона ОВ общая, стороны АВ и ВС равны как стороны многоугольника, а углы при вершине В равны [[Image:24-06-76.jpg]] Из равенства треугольников следует, что треугольник ОВС равнобедренный с углом при вершине С, равным [[Image:24-06-76.jpg]], т. е. СО есть биссектриса угла С.<br>Теперь соединяем точку О с вершиной D, соседней с С, и доказываем, что треугольник COD равнобедренный и DO — биссектриса угла D многоугольника. И т. д.<br> <br>В итоге получается, что каждый треугольник, у которого одна сторона есть сторона многоугольника, а противолежащая вершина — точка О, является равнобедренным. Все эти треугольники имеют равные боковые стороны и равные высоты, опущенные на их основания. Отсюда следует, что все вершины многоугольника находятся на окружности с центром О и радиусом, равным боковым сторонам треугольников, а все стороны многоугольника касаются окружности с центром О и радиусом, равным высотам треугольников, опущенным из вершины О. Теорема доказана. |
| | + | |
| | + | Вписанная и описанная окружности правильного многоугольника имеют один и тот же центр. Его называют центром многоугольника. Угол, под которым видна сторона правильного многоугольника из его центра, называется центральным углом многоугольника.<br><br>[[Image:24-06-77.jpg]]<br><br> |
| | | | |
| | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> | | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> |
Версия 13:17, 24 июня 2010
Гипермаркет знаний>>Математика>>Математика 9 класс>>Математика:Правильные многоугольники
ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ
Выпуклый многоугольник называется правильным, если у него все стороны равны и все углы равны.
Многоугольник называется вписанным в окружность, если все его вершины лежат на некоторой окружности. Многоугольник называется описанным около окружности, если все его стороны касаются некоторой окружности.
Теорема 13.3. Правильный выпуклый многоугольник является вписанным в окружность и описанным около окружности.
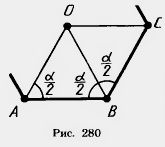
Доказательство. Пусть А и В — две соседние вершины правильного многоугольника (рис. 280). Проведем биссектрисы углов многоугольника из вершин А и В. Пусть О — точка их пересечения. Треугольник АОВ равнобедренный с основанием АВ и углами при основании, равными 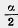 где где  —угол многоугольника. —угол многоугольника.
Соединим точку О с вершиной С, соседней с В. Треугольники АВО и СВО равны по первому признаку равенства треугольников. У них сторона ОВ общая, стороны АВ и ВС равны как стороны многоугольника, а углы при вершине В равны 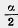 Из равенства треугольников следует, что треугольник ОВС равнобедренный с углом при вершине С, равным Из равенства треугольников следует, что треугольник ОВС равнобедренный с углом при вершине С, равным 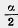 , т. е. СО есть биссектриса угла С. , т. е. СО есть биссектриса угла С.
Теперь соединяем точку О с вершиной D, соседней с С, и доказываем, что треугольник COD равнобедренный и DO — биссектриса угла D многоугольника. И т. д.
В итоге получается, что каждый треугольник, у которого одна сторона есть сторона многоугольника, а противолежащая вершина — точка О, является равнобедренным. Все эти треугольники имеют равные боковые стороны и равные высоты, опущенные на их основания. Отсюда следует, что все вершины многоугольника находятся на окружности с центром О и радиусом, равным боковым сторонам треугольников, а все стороны многоугольника касаются окружности с центром О и радиусом, равным высотам треугольников, опущенным из вершины О. Теорема доказана.
Вписанная и описанная окружности правильного многоугольника имеют один и тот же центр. Его называют центром многоугольника. Угол, под которым видна сторона правильного многоугольника из его центра, называется центральным углом многоугольника.
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Книги, учебники математике скачать, конспект на помощь учителю и ученикам, учиться онлайн
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|











