|
|
|
| Строка 5: |
Строка 5: |
| | <br> | | <br> |
| | | | |
| - | ''' ДЛИНА ОКРУЖНОСТИ''' | + | ''' ДЛИНА ОКРУЖНОСТИ''' |
| | | | |
| - | <br>Наглядное представление о длине окружности получается следующим образом. Представим себе нить в форме окружности. Разрежем ее и растянем за концы. Длина полученного отрезка и есть длина окружности. Как найти длину окружности, зная ее радиус? Ясно, что при неограниченном увеличении числа сторон вписанного в окружность правильного многоугольника его периметр неограниченно приближается к длине окружности (рис. 288). Исходя из этого, докажем некоторые свойства длины окружности. | + | <br>Наглядное представление о длине окружности получается следующим образом. Представим себе нить в форме окружности. Разрежем ее и растянем за концы. Длина полученного отрезка и есть длина окружности. Как найти длину окружности, зная ее радиус? Ясно, что при неограниченном увеличении числа сторон вписанного в окружность правильного многоугольника его периметр неограниченно приближается к длине окружности (рис. 288). Исходя из этого, докажем некоторые свойства длины окружности. |
| | | | |
| | + | <br> |
| | | | |
| | + | [[Image:24-06-89.jpg]] |
| | | | |
| - | [[Image:24-06-89.jpg]]
| + | <br> |
| | | | |
| | + | Теорема 13.5. '''''Отношение длины окружности к ее диаметру не зависит от окружности, т. е. одно и то же для любых двух окружностей.''''' |
| | | | |
| | + | <br>Доказательство. Возьмем две произвольные окружности. Пусть R<sub>1</sub> и R<sub>2</sub> — их радиусы, а l<sub>1</sub>, и I<sub>2</sub> — их длины.<br><br> |
| | | | |
| - | Теорема 13.5. '''''Отношение длины окружности к ее диаметру не зависит от окружности, т. е. одно и то же для любых двух окружностей.'''''
| + | Допустим, что утверждение теоремы неверно и [[Image:24-06-89.jpg]]<br>например: |
| | | | |
| - | <br>Доказательство. Возьмем две произвольные окружности. Пусть R<sub>1</sub> и R<sub>2</sub> — их радиусы, а l<sub>1</sub>, и I<sub>2</sub> — их длины.<br><br> | + | [[Image:24-06-90.jpg]]<br> <br>Впишем в наши окружности правильные выпуклые многоугольники с большим числом сторон n. Если n очень велико, то длины наших окружностей будут очень мало отличаться от периметров р<sub>1</sub> и р<sub>2</sub> вписанных многоугольников. Поэтому неравенство (*) не нарушится, если в нем заменить l<sub>1</sub> на р<sub>1</sub>, а l<sub>2</sub> на р<sub>2</sub>: |
| | | | |
| - | Допустим, что утверждение теоремы неверно и [[Image:24-06-89.jpg]]<br>например:
| + | [[Image:24-06-91.jpg]]<br><br>Но, как мы знаем, периметры правильных выпуклых n-угольников относятся как радиусы описанных окружностей: |
| | | | |
| - | [[Image:24-06-90.jpg]]<br> <br>Впишем в наши окружности правильные выпуклые многоугольники с большим числом сторон n. Если n очень велико, то длины наших окружностей будут очень мало отличаться от периметров р<sub>1</sub> и р<sub>2</sub> вписанных многоугольников. Поэтому неравенство (*) не нарушится, если в нем заменить l<sub>1</sub> на р<sub>1</sub>, а l<sub>2</sub> на р<sub>2</sub>: | + | [[Image:24-06-92.jpg]]<br><br>Отсюда [[Image:24-06-92.jpg]] А это противоречит неравенству (**). Теорема доказана. |
| | | | |
| - | [[Image:24-06-91.jpg]]<br><br>Но, как мы знаем, периметры правильных выпуклых n-угольников относятся как радиусы описанных окружностей: | + | Отношение длины окружности к диаметру принято обозначать греческой буквой [[Image:24-06-93.jpg]] (читается «пи»): |
| | | | |
| - | [[Image:24-06-92.jpg]]<br><br>Отсюда [[Image:24-06-92.jpg]] А это противоречит неравенству (**). Теорема доказана. | + | [[Image:24-06-94.jpg]]<br> <br>Число [[Image:24-06-93.jpg]] иррациональное. Приближенное значение |
| | | | |
| - | Отношение длины окружности к диаметру принято обозначать греческой буквой [[Image:24-06-93.jpg]] (читается «пи»):
| + | [[Image:24-06-95.jpg]]<br><br>Приближенное значение числа [[Image:24-06-93.jpg]] было известно уже древним грекам. Очень простое приближенное значение [[Image:24-06-93.jpg]] нашел Архимед: [[Image:24-06-96.jpg]] . Оно отличается от точного значения [[Image:24-06-93.jpg]] меньше чем на 0,002. |
| | | | |
| - | [[Image:24-06-94.jpg]]<br> <br>Число [[Image:24-06-93.jpg]] иррациональное. Приближенное значение
| |
| | | | |
| - | [[Image:24-06-95.jpg]]<br><br>Приближенное значение числа л было известно уже древним грекам. Очень простое приближенное значение л нашел 22<br>Архимед: — . Оно отличается от точного значения л меньше чем на 0,002.<br>Так как = л, то длина окружности<br>вычисляется по формуле<br><br><br> | + | |
| | + | [[Image:24-06-97.jpg]] |
| | + | |
| | + | <br>Так как [[Image:24-06-98.jpg]], то длина окружности вычисляется по формуле |
| | + | |
| | + | [[Image:24-06-99.jpg]]<br><br><br> |
| | | | |
| | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> | | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> |
Версия 19:02, 24 июня 2010
Гипермаркет знаний>>Математика>>Математика 9 класс>>Математика:Длина окружности
ДЛИНА ОКРУЖНОСТИ
Наглядное представление о длине окружности получается следующим образом. Представим себе нить в форме окружности. Разрежем ее и растянем за концы. Длина полученного отрезка и есть длина окружности. Как найти длину окружности, зная ее радиус? Ясно, что при неограниченном увеличении числа сторон вписанного в окружность правильного многоугольника его периметр неограниченно приближается к длине окружности (рис. 288). Исходя из этого, докажем некоторые свойства длины окружности.
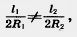
Теорема 13.5. Отношение длины окружности к ее диаметру не зависит от окружности, т. е. одно и то же для любых двух окружностей.
Доказательство. Возьмем две произвольные окружности. Пусть R1 и R2 — их радиусы, а l1, и I2 — их длины.
Допустим, что утверждение теоремы неверно и 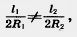
например:

Впишем в наши окружности правильные выпуклые многоугольники с большим числом сторон n. Если n очень велико, то длины наших окружностей будут очень мало отличаться от периметров р1 и р2 вписанных многоугольников. Поэтому неравенство (*) не нарушится, если в нем заменить l1 на р1, а l2 на р2:

Но, как мы знаем, периметры правильных выпуклых n-угольников относятся как радиусы описанных окружностей:
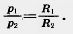
Отсюда 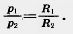 А это противоречит неравенству (**). Теорема доказана. А это противоречит неравенству (**). Теорема доказана.
Отношение длины окружности к диаметру принято обозначать греческой буквой 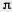 (читается «пи»): (читается «пи»):
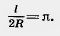
Число 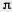 иррациональное. Приближенное значение иррациональное. Приближенное значение
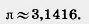
Приближенное значение числа 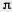 было известно уже древним грекам. Очень простое приближенное значение было известно уже древним грекам. Очень простое приближенное значение 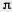 нашел Архимед: нашел Архимед: 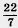 . Оно отличается от точного значения . Оно отличается от точного значения 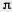 меньше чем на 0,002. меньше чем на 0,002.

Так как 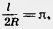 , то длина окружности вычисляется по формуле , то длина окружности вычисляется по формуле
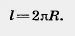
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Учебники и книги по всему предметам, домашняя работа, онлайн библиотеки книжек, планы конспектов уроков по математике, рефераты и конспекты уроков по математике для 9 класса скачать
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|











