|
|
|
| Строка 2: |
Строка 2: |
| | | | |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 9 класс|Математика 9 класс]]>>Математика:Понятие площади''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 9 класс|Математика 9 класс]]>>Математика:Понятие площади''' |
| - | <br>
| |
| - | '''ПОНЯТИЕ ПЛОЩАДИ'''
| |
| | | | |
| - | <br>'''''Геометрическую фигуру будем называть простой, если ее можно разбить на конечное число плоских треугольников'''''. Напомним, что '''''плоским треугольником мы называем конечную часть плоскости, ограниченную треугольником''''' (рис. 294).<br>Примером простой фигуры является выпуклый плоский многоугольник. Он разбивается на плоские треугольники диа-<br> <br>[[Image:29-06-16.jpg]]<br><br>гоналями, проведенными из какой-нибудь его вершины (рис. 295). В этом параграфе мы рассматриваем только плоские многоугольники и поэтому повторять каждый раз слово «плоский» не будем.
| |
| | | | |
| - | Дадим определение площади для простых фигур.
| |
| | | | |
| - | Для простых фигур '''''площадь — это положительная величина, численное значение которой обладает следующими свойствами:'''''
| + | <br> '''ПОНЯТИЕ ПЛОЩАДИ''' |
| | | | |
| - | 1) Равные фигуры имеют равные площади.
| + | <br>'''''Геометрическую фигуру будем называть простой, если ее можно разбить на конечное число плоских треугольников'''''. Напомним, что '''''плоским треугольником мы называем конечную часть плоскости, ограниченную треугольником''''' (рис. 294).<br>Примером простой фигуры является выпуклый плоский многоугольник. Он разбивается на плоские треугольники диа-<br> <br>[[Image:29-06-16.jpg]]<br><br>гоналями, проведенными из какой-нибудь его вершины (рис. 295). В этом параграфе мы рассматриваем только плоские многоугольники и поэтому повторять каждый раз слово «плоский» не будем. |
| | | | |
| - | 2) Если фигура разбивается на части, являющиеся простыми фигурами, то площадь этой фигуры равна сумме площадей ее частей.
| + | Дадим определение площади для простых фигур. |
| | | | |
| - | 3) Площадь квадрата со стороной, равной единице измерения, равна единице.
| + | Для простых фигур '''''площадь — это положительная величина, численное значение которой обладает следующими свойствами:''''' |
| | | | |
| - | Если квадрат, о котором идет речь в определении, имеет сторону 1 м, то площадь будет в квадратных метрах (м<sup>2</sup>). Если сторона квадрата 100 м, то площадь будет в гектарах. Если сторона квадрата 1 км, то площадь будет в квадратных километрах, и т. п.<br> | + | 1) Равные фигуры имеют равные площади. |
| | + | |
| | + | 2) Если фигура разбивается на части, являющиеся простыми фигурами, то площадь этой фигуры равна сумме площадей ее частей. |
| | + | |
| | + | 3) Площадь квадрата со стороной, равной единице измерения, равна единице. |
| | + | |
| | + | Если квадрат, о котором идет речь в определении, имеет сторону 1 м, то площадь будет в квадратных метрах (м<sup>2</sup>). Если сторона квадрата 100 м, то площадь будет в гектарах. Если сторона квадрата 1 км, то площадь будет в квадратных километрах, и т. п.<br> |
| | | | |
| | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> | | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> |
Версия 06:21, 29 июня 2010
Гипермаркет знаний>>Математика>>Математика 9 класс>>Математика:Понятие площади
ПОНЯТИЕ ПЛОЩАДИ
Геометрическую фигуру будем называть простой, если ее можно разбить на конечное число плоских треугольников. Напомним, что плоским треугольником мы называем конечную часть плоскости, ограниченную треугольником (рис. 294).
Примером простой фигуры является выпуклый плоский многоугольник. Он разбивается на плоские треугольники диа-
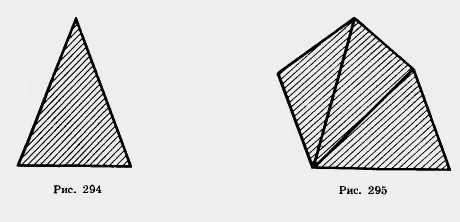
гоналями, проведенными из какой-нибудь его вершины (рис. 295). В этом параграфе мы рассматриваем только плоские многоугольники и поэтому повторять каждый раз слово «плоский» не будем.
Дадим определение площади для простых фигур.
Для простых фигур площадь — это положительная величина, численное значение которой обладает следующими свойствами:
1) Равные фигуры имеют равные площади.
2) Если фигура разбивается на части, являющиеся простыми фигурами, то площадь этой фигуры равна сумме площадей ее частей.
3) Площадь квадрата со стороной, равной единице измерения, равна единице.
Если квадрат, о котором идет речь в определении, имеет сторону 1 м, то площадь будет в квадратных метрах (м2). Если сторона квадрата 100 м, то площадь будет в гектарах. Если сторона квадрата 1 км, то площадь будет в квадратных километрах, и т. п.
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Календарно-тематическое планирование по математике, задачи и ответы школьнику онлайн, курсы учителю по математике скачать
Содержание урока
 конспект урока
опорный каркас
презентация урока
акселеративные методы
интерактивные технологии
Практика
задачи и упражнения
самопроверка
практикумы, тренинги, кейсы, квесты
домашние задания
дискуссионные вопросы
риторические вопросы от учеников
Иллюстрации
аудио-, видеоклипы и мультимедиа
фотографии, картинки
графики, таблицы, схемы
юмор, анекдоты, приколы, комиксы
притчи, поговорки, кроссворды, цитаты
Дополнения
рефераты
статьи
фишки для любознательных
шпаргалки
учебники основные и дополнительные
словарь терминов
прочие
Совершенствование учебников и уроков
исправление ошибок в учебнике
обновление фрагмента в учебнике
элементы новаторства на уроке
замена устаревших знаний новыми
Только для учителей
идеальные уроки
календарный план на год
методические рекомендации
программы
обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|
