|
|
|
| Строка 7: |
Строка 7: |
| | ''' 17. Деление'''<br><br>Задача. Площадь прямоугольника [[Image:20-07-368.jpg]] м<sup>2</sup> . Длина одной стороны [[Image:20-07-369.jpg]] м. Найдем длину другой стороны. | | ''' 17. Деление'''<br><br>Задача. Площадь прямоугольника [[Image:20-07-368.jpg]] м<sup>2</sup> . Длина одной стороны [[Image:20-07-369.jpg]] м. Найдем длину другой стороны. |
| | | | |
| - | Решение. Обозначим длину другой стороны через х м. По формуле площади прямоугольника должно выполняться равенство [[Image:20-07-369.jpg]]х= [[Image:20-07-368.jpg]] Умножим обе части равенства на число [[Image:20-07-370.jpg]] обратное числу [[Image:20-07-369.jpg]]. Так как произведение [[Image:20-07-369.jpg]]•—равно 1, то полу-<br>4 4 3<br>чим, что дс=у~ —, или х = ^ . Таким образом, длина другой<br>20<br>стороны прямоугольника равна — м.<br>В этой задаче мы нашли неизвестный множитель в произ-<br>3 5<br>ведении — • д:——. По смыслу деления это число равно част-<br>5 3 «<br>ному от деления числа — на число —. Видим, что это частное<br>равно произведению делимого и числа, обратного делителю, т. е.<br>5 . 3 _ 5 4 _ 20 7 ' 4 _ 7 ' 3 _ 21'<br>Чтобы разделить одну дробь на другую, надо делимое умножить на число, обратное делителю.<br>2 1<br>Пример 1. Разделим 2 — на 1 — .<br>О 1и<br>2 1<br>Решение. Представим сначала числа 2 — и 1 — в виде не-<br>л „ „ 2 12 Л 1 16 правильных дробей: 2 —=— ; 1 — =— .<br>тт о 2 ., 1 12.16 12 15 12 15 3-3 9 „ 1<br>Поэтому 2y.l-=T.-=T.-=—=Т=Т=2Т.<br>Пример 2. Разделим — на 6.<br>О<br>О<br>о<br>Решение. Числом, обратным делителю, является , так как 6"i-=l. Значит, .<br>Сформулируйте правило деления дробей. Как выполняется деление смешанных чисел?<br>580. Выполните деление:<br>")f:f: ")f:f= д>-Н?: ж>т:3= <br><br>и) 8:f; М>4Т: T)0:5-L;<br>к)<br>7 2 H)lf: Р) 4-f-:»; У) 3-^:1;<br>л> Зт:т: о) ю f 0 ф) 3-!:i_L 39 31<br><br>D<br> Частное двух дробей можно читать разными способами: 2 .11<br>—:— — две седьмых разделить на и. п.<br>одиннадцать четырнадцатых;<br>в. п.<br>— частное чисел две седьмых и<br>в. п.<br>одиннадцать четырнадцатых; в. п.<br>— частное двух седьмых и<br>р. п.<br>одиннадцати четырнадцатых.<br>р. п.<br>581. Представьте в виде дроби частное:<br>a) -2L:J2-; б) в) г)<br>пк b а к п i<br>582. Найдите по формуле площади прямоугольника S—ab значение:<br>a) S, если а—44- и Ь=-~; б) а, если <S=15 и Ь — 7—.<br>6 7' 2<br>583. С какой скоростью должен передвигаться трактор,<br>чтобы пройти 15 км за 4~ ч; за ч?<br>в з<br>584. За 4- кг сухарей заплатили -§- р. Сколько стоит 1 кг<br>б 5<br>сухарей? Сколько сухарей можно купить на 1 р.?<br>585. Сумма двух чисел равна 12 Одно из них в 1 раза больше другого. Найдите эти числа.<br>586. Если задуманное число умножить на 2 ^ и к произве-<br>С с<br>дению прибавить 1 , то получится 8 — . Найдите задуманное число.<br>587. Площадь прямоугольника м2. Найдите периметр<br>64<br>прямоугольника, если его ширина м.<br>о<br>588. Длина и ширина прямоугольника соответственно рав-<br>ны5-§-ми2-§-м. Найдите ширину другого прямоугольника,<br>5 8<br>длина которого 3 м, а площадь равна площади первого<br>5<br>прямоугольника.<br>589. Представьте делимое в виде обыкновенной дроби<br>3 2<br>и выполните действие: а) 0,25: —; б) 0,6: — .<br>4 5<br>590. Представьте делимое в виде десятичной дроби и<br>Л О<br>выполните действие: а) —:0,2; б) —:0,375.<br>25 8<br>591. Выполните действия:<br>"> т-т-Ь ):2 +<br>«гЛЬ ")(2f+1f +<br>&)(2f+lf).li: M,(ei-}):(3l+li).<br>592. Найдите значение выражения:<br>а) (т^0,25 + |-):1^; в) 6,25 8-^-3|-:5,5 + 2,4 4^ ;<br>б) 8:0,16 —3 6,4; г) ((l J-)2-1,6 ): 0,12. <br><br>593. Решите уравнение:<br>а) -2-х —2-2-; ж) m + =<br>r)3-|-:*=li-:2; Ю 3f (f *+f )=2-L;<br>2<br>594. Коля и Митя нашли 64 гриба. Коля нашел в 1 — раза больше грибов, чем Митя. Сколько грибов нашел каждый?<br>595. Луч ОМ разделил угол СОК, равный 90°, на два угла<br>СОМ и МОК. Угол СОМ больше угла МОК в 2 -f- раза. Чему рав-<br>5<br>ны углы СОМ и МОК? Постройте эти углы с помощью транспортира.<br>596. Отец старше сына в 3 -J- раза, а сын моложе отца на<br>О<br>28 лет. Сколько лет отцу и сколько лет сыну?<br>597. За два дня турист прошел 26 км. Путь, пройденный<br>g<br>в первый день, составлял — пути, пройденного во второй день.<br>Сколько километров прошел турист в каждый из этих дней?<br>598. Месячный заработок сына составил 75% заработка отца. Сколько заработал каждый из них, если вместе они заработали 350 р.?<br>599. Первый плотник сделал на 9 оконных рам меньше, чем второй. Сколько рам сделал каждый плотник, если число рам,<br>5<br>сделанных первым плотником, составляет -—- числа рам, сделан-<br>о<br>ных вторым?<br>600. Два пешехода вышли одновременно навстречу друг другу из двух пунктов, расстояние между которыми 5 км. Ско-<br>2<br>рость первого пешехода составляла — скорости второго. Най-<br>з<br>J_ •2*<br>3 <br>1 1<br>3 3 ;<br> <br> * 14 '<br>2<br>. 3<br>дите скорости каждого пешехода, если они встретились через полчаса. <br> <br>601. Мотоциклист стал догонять велосипедиста, когда<br>3 <br>между ними было 33 км, и догнал его через — ч. Известно, что<br>4 <br>скорость велосипедиста составляла -гт скорости мотоциклиста.<br>14<br>Найдите скорости мотоциклиста и велосипедиста.<br>3 1<br>602. За 8 — м сукна и 7 — м сатина заплатили 225 р.<br>Сколько стоит 1 м сатина и сколько стоит 1 м сукна, если за сукно заплатили в 14 раз больше, чем за сатин?<br>603. За 32 м ткани и 20 м клеенки заплатили 80 р. Стои-<br>2<br>мость ткани составила — стоимости клеенки. Что дороже: 1 м<br>о<br>ткани или 1 м клеенки? На' сколько рублей?<br>604. Турист 3 ч шел пешком со скоростью 5 км/ч, а далее 4 ч он ехал на поезде, скорость которого в 12 раз больше. Оставшийся путь турист проехал на автобусе за 8 ч. С какой средней скоростью двигался турист за время путешествия, если<br>скорость автобуса составляла скорости поезда?<br>О<br>^^ 605. Вычислите устно:<br>а) 184-112 б) 700 : 14 в) 0,64 : 0,8 г) 3,6 • 0,1 д) 1-0,44<br>: 8 -9 -9 :0,6 : 0,7<br>-1-45 +90 +2,8 +3,6 ¦ 0,5<br>: 3 : 18 : 100 : 1,4 -0,12 <br><br>Подумайте, какие натуральные числа являются решениями неравенства:<br>а) *<4; б) 5<дс<9; в) 3<х<5.<br>610. Найдите число, обратное числу:<br>а)|-; 6)4; в)3-|-; г) 0,8; д) 1,4.<br>611. Докажите, что числа а и Ъ взаимно обратны, если: а) а = 0,5, Ъ = 2; б) а=1,25, Ь=-|-; в) а = 0,15, Ь = б|-.<br>612. Выполните деление и результат округлите до сотых: а) 3,2:0,7; б) 14,28:3,6; в) 175:23; г) 0,00677:1,3.<br>613. Округлите числа:<br>а) 0,479; 1,071; 2,750; 4,4981 до десятых;<br>б) 0,0825; 0,8537; 1,3576; 4,57003 до тысячных.<br>614. Баян стоил 106 р. Сколько стал стоить баян после снижения его цены на 15%?<br>615. Решите задачу:<br>1) Из 250 лошадей было 30 вороных, а 0,7 всех лошадей были серыми. Кроме вороных и серых, были лишь лошади рыжей масти. Сколько было лошадей рыжей масти?<br>2) Купили 120 тюбиков клея. Из них в 30 тюбиках был резиновый клей, а в 0,4 остальных тюбиков был казеиновый клей. Кроме резинового и казеинового клея, был куплен и силикатный клей. Сколько тюбиков силикатного клея было куплено?<br>616. Решите уравнение:<br>1) (0,2* + 0,4х)-3,5 = 6,3; 3) {х—0,2х):0,4 = 1,6;<br>2) (0,7х — 0,2jc) • 6,4 = 9,6; 4) (0,4* +дс): 0,7 = 1,6.<br>Щ 617. Выполните деление:<br>а) -Н-; в) JJJ:д) 8:-f-; ж) 2f:lii;„) 2А:7§;<br>б>-Иг: г) §1:9; е) 7:3; а) 3 f: 1 |i ; к) 2 12 f.<br>618. Найдите значение выражения:<br>a) 7j-:4f.8;6) 11^:4};») lf'2f:lf; г) .<br>619. Выполните действия:<br>97<br>а> т:т+ т-т-1:1т-<br>4 Зак. 607 <br><br>е) ((i j-j'-f)^.<br>620. Решите уравнение:<br>а) (*_8)~§—2; б) 2 2 ^=2 -1-.<br>621. Сколько оборотов сделает колесо на расстоянии 48 м,<br>б з 4 о<br>если длина окружности колеса равна — м; — м; —- м?<br>Zo 4 5<br>2 2<br>622. За —- ч мотоциклист проехал 20 — км. С какой ско-<br>3 5<br>ростью ехал мотоциклист?<br>623. На изготовлейие 16 одинаковых деталей требуется<br>п<br>6 — ч. Сколько времени занимает изготовление одной детали?<br>О<br>624. В двух сосудах 35 л жидкости. Известно, что в одном<br>сосуде жидкости в 1-^- раза меньше, чем в другом. Сколько<br>з<br>жидкости в каждом сосуде?<br>625. В двух пачках 156 тетрадей. Число тетрадей в одной<br>с<br>пачке составляет — числа тетрадей другой пачки. Сколько<br>тетрадей в каждой пачке?<br>626. Стоимость зимнего пальто на 84 р. больше стоимости летнего пальто. Сколько стоит каждое пальто, если стоимость летнего пальто составляет 60% стоимости зимнего?<br>627. Два катера движутся навстречу друг другу. Сейчас<br>7<br>между ними 25 км. Скорость одного из них составляет — ско-<br>о<br>г<br>рости другого. Найдите скорость каждого катера, если известно, что они встретятся через ч.<br>628. Турист ехал на автобусе 1 4- ч и на поезде 4-^- ч.<br>о 15<br>Всего этими видами транспорта турист проехал 456 км. При<br>g<br>этом на автобусе он проехал — того пути, который он проехал<br>на поезде. С какой скоростью турист ехал на автобусе и с какой — на поезде?<br>629. Выполните деление и округлите ответ до тысячных: а) 1,765:1,3; б) 5,394:23; в) 2,6:11,2.<br>630. Вычислите:<br>а) 74:100-0,4:10 + 17,8:1000;<br>б) 0,35 • 10 + 0,0237 • 100 - 0,00087 1000;<br>в) 37-0,01-0,2-0,1 + 8,9-Х),001;<br>г) 0,7:0,1 + 0,0474:0,01 — 0,00174:0,001.<br><br><br><br><br>
| + | Решение. Обозначим длину другой стороны через х м. По формуле площади прямоугольника должно выполняться равенство [[Image:20-07-369.jpg]]х= [[Image:20-07-368.jpg]] Умножим обе части равенства на число [[Image:20-07-370.jpg]] обратное числу [[Image:20-07-369.jpg]]. Так как произведение [[Image:20-07-369.jpg]]•[[Image:20-07-370.jpg]]равно 1, то получим, что х=[[Image:20-07-368.jpg]] •[[Image:20-07-370.jpg]], или х = [[Image:20-07-371.jpg]] . Таким образом, длина другой<br>стороны прямоугольника равна [[Image:20-07-371.jpg]] м. |
| | + | |
| | + | В этой задаче мы нашли неизвестный множитель в произведении [[Image:20-07-369.jpg]] • х=[[Image:20-07-368.jpg]]. По смыслу деления это число равно частному от деления числа [[Image:20-07-368.jpg]] на число [[Image:20-07-369.jpg]]. Видим, что это частное равно произведению делимого и числа, обратного делителю, т. е. |
| | + | |
| | + | [[Image:20-07-368.jpg]]:[[Image:20-07-369.jpg]]=[[Image:20-07-368.jpg]]•[[Image:20-07-370.jpg]]=[[Image:20-07-371.jpg]]<br><br>'''''Чтобы разделить одну дробь на другую, надо делимое умножить на число, обратное делителю.'''''<br><u><br>Пример 1.</u> Разделим 2[[Image:20-07-372.jpg]] на 1 [[Image:20-07-373.jpg]] .<br>Решение. Представим сначала числа 2 — и 1 — в виде не-<br>л „ „ 2 12 Л 1 16 правильных дробей: 2 —=— ; 1 — =— .<br>тт о 2 ., 1 12.16 12 15 12 15 3-3 9 „ 1<br>Поэтому 2y.l-=T.-=T.-=—=Т=Т=2Т.<br>Пример 2. Разделим — на 6.<br>О<br>О<br>о<br>Решение. Числом, обратным делителю, является , так как 6"i-=l. Значит, .<br>Сформулируйте правило деления дробей. Как выполняется деление смешанных чисел?<br>580. Выполните деление:<br>")f:f: ")f:f= д>-Н?: ж>т:3= <br><br>и) 8:f; М>4Т: T)0:5-L;<br>к)<br>7 2 H)lf: Р) 4-f-:»; У) 3-^:1;<br>л> Зт:т: о) ю f 0 ф) 3-!:i_L 39 31<br><br>D<br> Частное двух дробей можно читать разными способами: 2 .11<br>—:— — две седьмых разделить на и. п.<br>одиннадцать четырнадцатых;<br>в. п.<br>— частное чисел две седьмых и<br>в. п.<br>одиннадцать четырнадцатых; в. п.<br>— частное двух седьмых и<br>р. п.<br>одиннадцати четырнадцатых.<br>р. п.<br>581. Представьте в виде дроби частное:<br>a) -2L:J2-; б) в) г)<br>пк b а к п i<br>582. Найдите по формуле площади прямоугольника S—ab значение:<br>a) S, если а—44- и Ь=-~; б) а, если <S=15 и Ь — 7—.<br>6 7' 2<br>583. С какой скоростью должен передвигаться трактор,<br>чтобы пройти 15 км за 4~ ч; за ч?<br>в з<br>584. За 4- кг сухарей заплатили -§- р. Сколько стоит 1 кг<br>б 5<br>сухарей? Сколько сухарей можно купить на 1 р.?<br>585. Сумма двух чисел равна 12 Одно из них в 1 раза больше другого. Найдите эти числа.<br>586. Если задуманное число умножить на 2 ^ и к произве-<br>С с<br>дению прибавить 1 , то получится 8 — . Найдите задуманное число.<br>587. Площадь прямоугольника м2. Найдите периметр<br>64<br>прямоугольника, если его ширина м.<br>о<br>588. Длина и ширина прямоугольника соответственно рав-<br>ны5-§-ми2-§-м. Найдите ширину другого прямоугольника,<br>5 8<br>длина которого 3 м, а площадь равна площади первого<br>5<br>прямоугольника.<br>589. Представьте делимое в виде обыкновенной дроби<br>3 2<br>и выполните действие: а) 0,25: —; б) 0,6: — .<br>4 5<br>590. Представьте делимое в виде десятичной дроби и<br>Л О<br>выполните действие: а) —:0,2; б) —:0,375.<br>25 8<br>591. Выполните действия:<br>"> т-т-Ь ):2 +<br>«гЛЬ ")(2f+1f +<br>&)(2f+lf).li: M,(ei-}):(3l+li).<br>592. Найдите значение выражения:<br>а) (т^0,25 + |-):1^; в) 6,25 8-^-3|-:5,5 + 2,4 4^ ;<br>б) 8:0,16 —3 6,4; г) ((l J-)2-1,6 ): 0,12. <br><br>593. Решите уравнение:<br>а) -2-х —2-2-; ж) m + =<br>r)3-|-:*=li-:2; Ю 3f (f *+f )=2-L;<br>2<br>594. Коля и Митя нашли 64 гриба. Коля нашел в 1 — раза больше грибов, чем Митя. Сколько грибов нашел каждый?<br>595. Луч ОМ разделил угол СОК, равный 90°, на два угла<br>СОМ и МОК. Угол СОМ больше угла МОК в 2 -f- раза. Чему рав-<br>5<br>ны углы СОМ и МОК? Постройте эти углы с помощью транспортира.<br>596. Отец старше сына в 3 -J- раза, а сын моложе отца на<br>О<br>28 лет. Сколько лет отцу и сколько лет сыну?<br>597. За два дня турист прошел 26 км. Путь, пройденный<br>g<br>в первый день, составлял — пути, пройденного во второй день.<br>Сколько километров прошел турист в каждый из этих дней?<br>598. Месячный заработок сына составил 75% заработка отца. Сколько заработал каждый из них, если вместе они заработали 350 р.?<br>599. Первый плотник сделал на 9 оконных рам меньше, чем второй. Сколько рам сделал каждый плотник, если число рам,<br>5<br>сделанных первым плотником, составляет -—- числа рам, сделан-<br>о<br>ных вторым?<br>600. Два пешехода вышли одновременно навстречу друг другу из двух пунктов, расстояние между которыми 5 км. Ско-<br>2<br>рость первого пешехода составляла — скорости второго. Най-<br>з<br>J_ •2*<br>3 <br>1 1<br>3 3 ;<br> <br> * 14 '<br>2<br>. 3<br>дите скорости каждого пешехода, если они встретились через полчаса. <br> <br>601. Мотоциклист стал догонять велосипедиста, когда<br>3 <br>между ними было 33 км, и догнал его через — ч. Известно, что<br>4 <br>скорость велосипедиста составляла -гт скорости мотоциклиста.<br>14<br>Найдите скорости мотоциклиста и велосипедиста.<br>3 1<br>602. За 8 — м сукна и 7 — м сатина заплатили 225 р.<br>Сколько стоит 1 м сатина и сколько стоит 1 м сукна, если за сукно заплатили в 14 раз больше, чем за сатин?<br>603. За 32 м ткани и 20 м клеенки заплатили 80 р. Стои-<br>2<br>мость ткани составила — стоимости клеенки. Что дороже: 1 м<br>о<br>ткани или 1 м клеенки? На' сколько рублей?<br>604. Турист 3 ч шел пешком со скоростью 5 км/ч, а далее 4 ч он ехал на поезде, скорость которого в 12 раз больше. Оставшийся путь турист проехал на автобусе за 8 ч. С какой средней скоростью двигался турист за время путешествия, если<br>скорость автобуса составляла скорости поезда?<br>О<br>^^ 605. Вычислите устно:<br>а) 184-112 б) 700 : 14 в) 0,64 : 0,8 г) 3,6 • 0,1 д) 1-0,44<br>: 8 -9 -9 :0,6 : 0,7<br>-1-45 +90 +2,8 +3,6 ¦ 0,5<br>: 3 : 18 : 100 : 1,4 -0,12 <br><br>Подумайте, какие натуральные числа являются решениями неравенства:<br>а) *<4; б) 5<дс<9; в) 3<х<5.<br>610. Найдите число, обратное числу:<br>а)|-; 6)4; в)3-|-; г) 0,8; д) 1,4.<br>611. Докажите, что числа а и Ъ взаимно обратны, если: а) а = 0,5, Ъ = 2; б) а=1,25, Ь=-|-; в) а = 0,15, Ь = б|-.<br>612. Выполните деление и результат округлите до сотых: а) 3,2:0,7; б) 14,28:3,6; в) 175:23; г) 0,00677:1,3.<br>613. Округлите числа:<br>а) 0,479; 1,071; 2,750; 4,4981 до десятых;<br>б) 0,0825; 0,8537; 1,3576; 4,57003 до тысячных.<br>614. Баян стоил 106 р. Сколько стал стоить баян после снижения его цены на 15%?<br>615. Решите задачу:<br>1) Из 250 лошадей было 30 вороных, а 0,7 всех лошадей были серыми. Кроме вороных и серых, были лишь лошади рыжей масти. Сколько было лошадей рыжей масти?<br>2) Купили 120 тюбиков клея. Из них в 30 тюбиках был резиновый клей, а в 0,4 остальных тюбиков был казеиновый клей. Кроме резинового и казеинового клея, был куплен и силикатный клей. Сколько тюбиков силикатного клея было куплено?<br>616. Решите уравнение:<br>1) (0,2* + 0,4х)-3,5 = 6,3; 3) {х—0,2х):0,4 = 1,6;<br>2) (0,7х — 0,2jc) • 6,4 = 9,6; 4) (0,4* +дс): 0,7 = 1,6.<br>Щ 617. Выполните деление:<br>а) -Н-; в) JJJ:д) 8:-f-; ж) 2f:lii;„) 2А:7§;<br>б>-Иг: г) §1:9; е) 7:3; а) 3 f: 1 |i ; к) 2 12 f.<br>618. Найдите значение выражения:<br>a) 7j-:4f.8;6) 11^:4};») lf'2f:lf; г) .<br>619. Выполните действия:<br>97<br>а> т:т+ т-т-1:1т-<br>4 Зак. 607 <br><br>е) ((i j-j'-f)^.<br>620. Решите уравнение:<br>а) (*_8)~§—2; б) 2 2 ^=2 -1-.<br>621. Сколько оборотов сделает колесо на расстоянии 48 м,<br>б з 4 о<br>если длина окружности колеса равна — м; — м; —- м?<br>Zo 4 5<br>2 2<br>622. За —- ч мотоциклист проехал 20 — км. С какой ско-<br>3 5<br>ростью ехал мотоциклист?<br>623. На изготовлейие 16 одинаковых деталей требуется<br>п<br>6 — ч. Сколько времени занимает изготовление одной детали?<br>О<br>624. В двух сосудах 35 л жидкости. Известно, что в одном<br>сосуде жидкости в 1-^- раза меньше, чем в другом. Сколько<br>з<br>жидкости в каждом сосуде?<br>625. В двух пачках 156 тетрадей. Число тетрадей в одной<br>с<br>пачке составляет — числа тетрадей другой пачки. Сколько<br>тетрадей в каждой пачке?<br>626. Стоимость зимнего пальто на 84 р. больше стоимости летнего пальто. Сколько стоит каждое пальто, если стоимость летнего пальто составляет 60% стоимости зимнего?<br>627. Два катера движутся навстречу друг другу. Сейчас<br>7<br>между ними 25 км. Скорость одного из них составляет — ско-<br>о<br>г<br>рости другого. Найдите скорость каждого катера, если известно, что они встретятся через ч.<br>628. Турист ехал на автобусе 1 4- ч и на поезде 4-^- ч.<br>о 15<br>Всего этими видами транспорта турист проехал 456 км. При<br>g<br>этом на автобусе он проехал — того пути, который он проехал<br>на поезде. С какой скоростью турист ехал на автобусе и с какой — на поезде?<br>629. Выполните деление и округлите ответ до тысячных: а) 1,765:1,3; б) 5,394:23; в) 2,6:11,2.<br>630. Вычислите:<br>а) 74:100-0,4:10 + 17,8:1000;<br>б) 0,35 • 10 + 0,0237 • 100 - 0,00087 1000;<br>в) 37-0,01-0,2-0,1 + 8,9-Х),001;<br>г) 0,7:0,1 + 0,0474:0,01 — 0,00174:0,001.<br><br><br><br><br> |
| | | | |
| | <br> ''Н.Я.Виленкин, А.С. Чесноков, С.И. Шварцбурд, В.И.Жохов, Математика для 6 класса, Учебник для средней школы'' <br> | | <br> ''Н.Я.Виленкин, А.С. Чесноков, С.И. Шварцбурд, В.И.Жохов, Математика для 6 класса, Учебник для средней школы'' <br> |
Версия 17:23, 20 июля 2010
Гипермаркет знаний>>Математика>>Математика 6 класс>>Математика: Деление-6 класс
17. Деление
Задача. Площадь прямоугольника 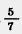 м2 . Длина одной стороны м2 . Длина одной стороны 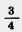 м. Найдем длину другой стороны. м. Найдем длину другой стороны.
Решение. Обозначим длину другой стороны через х м. По формуле площади прямоугольника должно выполняться равенство 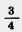 х= х= 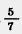 Умножим обе части равенства на число Умножим обе части равенства на число 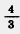 обратное числу обратное числу 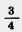 . Так как произведение . Так как произведение 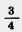 • •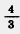 равно 1, то получим, что х= равно 1, то получим, что х=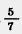 • •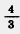 , или х = , или х = 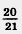 . Таким образом, длина другой . Таким образом, длина другой
стороны прямоугольника равна 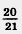 м. м.
В этой задаче мы нашли неизвестный множитель в произведении 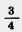 • х= • х=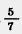 . По смыслу деления это число равно частному от деления числа . По смыслу деления это число равно частному от деления числа 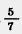 на число на число 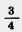 . Видим, что это частное равно произведению делимого и числа, обратного делителю, т. е. . Видим, что это частное равно произведению делимого и числа, обратного делителю, т. е.
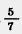 : :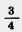 = =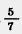 • •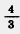 = =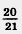
Чтобы разделить одну дробь на другую, надо делимое умножить на число, обратное делителю.
Пример 1. Разделим 2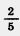 на 1 на 1 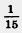 . .
Решение. Представим сначала числа 2 — и 1 — в виде не-
л „ „ 2 12 Л 1 16 правильных дробей: 2 —=— ; 1 — =— .
тт о 2 ., 1 12.16 12 15 12 15 3-3 9 „ 1
Поэтому 2y.l-=T.-=T.-=—=Т=Т=2Т.
Пример 2. Разделим — на 6.
О
О
о
Решение. Числом, обратным делителю, является , так как 6"i-=l. Значит, .
Сформулируйте правило деления дробей. Как выполняется деление смешанных чисел?
580. Выполните деление:
")f:f: ")f:f= д>-Н?: ж>т:3=
и) 8:f; М>4Т: T)0:5-L;
к)
7 2 H)lf: Р) 4-f-:»; У) 3-^:1;
л> Зт:т: о) ю f 0 ф) 3-!:i_L 39 31
D
Частное двух дробей можно читать разными способами: 2 .11
—:— — две седьмых разделить на и. п.
одиннадцать четырнадцатых;
в. п.
— частное чисел две седьмых и
в. п.
одиннадцать четырнадцатых; в. п.
— частное двух седьмых и
р. п.
одиннадцати четырнадцатых.
р. п.
581. Представьте в виде дроби частное:
a) -2L:J2-; б) в) г)
пк b а к п i
582. Найдите по формуле площади прямоугольника S—ab значение:
a) S, если а—44- и Ь=-~; б) а, если <S=15 и Ь — 7—.
6 7' 2
583. С какой скоростью должен передвигаться трактор,
чтобы пройти 15 км за 4~ ч; за ч?
в з
584. За 4- кг сухарей заплатили -§- р. Сколько стоит 1 кг
б 5
сухарей? Сколько сухарей можно купить на 1 р.?
585. Сумма двух чисел равна 12 Одно из них в 1 раза больше другого. Найдите эти числа.
586. Если задуманное число умножить на 2 ^ и к произве-
С с
дению прибавить 1 , то получится 8 — . Найдите задуманное число.
587. Площадь прямоугольника м2. Найдите периметр
64
прямоугольника, если его ширина м.
о
588. Длина и ширина прямоугольника соответственно рав-
ны5-§-ми2-§-м. Найдите ширину другого прямоугольника,
5 8
длина которого 3 м, а площадь равна площади первого
5
прямоугольника.
589. Представьте делимое в виде обыкновенной дроби
3 2
и выполните действие: а) 0,25: —; б) 0,6: — .
4 5
590. Представьте делимое в виде десятичной дроби и
Л О
выполните действие: а) —:0,2; б) —:0,375.
25 8
591. Выполните действия:
"> т-т-Ь ):2 +
«гЛЬ ")(2f+1f +
&)(2f+lf).li: M,(ei-}):(3l+li).
592. Найдите значение выражения:
а) (т^0,25 + |-):1^; в) 6,25 8-^-3|-:5,5 + 2,4 4^ ;
б) 8:0,16 —3 6,4; г) ((l J-)2-1,6 ): 0,12.
593. Решите уравнение:
а) -2-х —2-2-; ж) m + =
r)3-|-:*=li-:2; Ю 3f (f *+f )=2-L;
2
594. Коля и Митя нашли 64 гриба. Коля нашел в 1 — раза больше грибов, чем Митя. Сколько грибов нашел каждый?
595. Луч ОМ разделил угол СОК, равный 90°, на два угла
СОМ и МОК. Угол СОМ больше угла МОК в 2 -f- раза. Чему рав-
5
ны углы СОМ и МОК? Постройте эти углы с помощью транспортира.
596. Отец старше сына в 3 -J- раза, а сын моложе отца на
О
28 лет. Сколько лет отцу и сколько лет сыну?
597. За два дня турист прошел 26 км. Путь, пройденный
g
в первый день, составлял — пути, пройденного во второй день.
Сколько километров прошел турист в каждый из этих дней?
598. Месячный заработок сына составил 75% заработка отца. Сколько заработал каждый из них, если вместе они заработали 350 р.?
599. Первый плотник сделал на 9 оконных рам меньше, чем второй. Сколько рам сделал каждый плотник, если число рам,
5
сделанных первым плотником, составляет -—- числа рам, сделан-
о
ных вторым?
600. Два пешехода вышли одновременно навстречу друг другу из двух пунктов, расстояние между которыми 5 км. Ско-
2
рость первого пешехода составляла — скорости второго. Най-
з
J_ •2*
3
1 1
3 3 ;
* 14 '
2
. 3
дите скорости каждого пешехода, если они встретились через полчаса.
601. Мотоциклист стал догонять велосипедиста, когда
3
между ними было 33 км, и догнал его через — ч. Известно, что
4
скорость велосипедиста составляла -гт скорости мотоциклиста.
14
Найдите скорости мотоциклиста и велосипедиста.
3 1
602. За 8 — м сукна и 7 — м сатина заплатили 225 р.
Сколько стоит 1 м сатина и сколько стоит 1 м сукна, если за сукно заплатили в 14 раз больше, чем за сатин?
603. За 32 м ткани и 20 м клеенки заплатили 80 р. Стои-
2
мость ткани составила — стоимости клеенки. Что дороже: 1 м
о
ткани или 1 м клеенки? На' сколько рублей?
604. Турист 3 ч шел пешком со скоростью 5 км/ч, а далее 4 ч он ехал на поезде, скорость которого в 12 раз больше. Оставшийся путь турист проехал на автобусе за 8 ч. С какой средней скоростью двигался турист за время путешествия, если
скорость автобуса составляла скорости поезда?
О
^^ 605. Вычислите устно:
а) 184-112 б) 700 : 14 в) 0,64 : 0,8 г) 3,6 • 0,1 д) 1-0,44
: 8 -9 -9 :0,6 : 0,7
-1-45 +90 +2,8 +3,6 ¦ 0,5
: 3 : 18 : 100 : 1,4 -0,12
Подумайте, какие натуральные числа являются решениями неравенства:
а) *<4; б) 5<дс<9; в) 3<х<5.
610. Найдите число, обратное числу:
а)|-; 6)4; в)3-|-; г) 0,8; д) 1,4.
611. Докажите, что числа а и Ъ взаимно обратны, если: а) а = 0,5, Ъ = 2; б) а=1,25, Ь=-|-; в) а = 0,15, Ь = б|-.
612. Выполните деление и результат округлите до сотых: а) 3,2:0,7; б) 14,28:3,6; в) 175:23; г) 0,00677:1,3.
613. Округлите числа:
а) 0,479; 1,071; 2,750; 4,4981 до десятых;
б) 0,0825; 0,8537; 1,3576; 4,57003 до тысячных.
614. Баян стоил 106 р. Сколько стал стоить баян после снижения его цены на 15%?
615. Решите задачу:
1) Из 250 лошадей было 30 вороных, а 0,7 всех лошадей были серыми. Кроме вороных и серых, были лишь лошади рыжей масти. Сколько было лошадей рыжей масти?
2) Купили 120 тюбиков клея. Из них в 30 тюбиках был резиновый клей, а в 0,4 остальных тюбиков был казеиновый клей. Кроме резинового и казеинового клея, был куплен и силикатный клей. Сколько тюбиков силикатного клея было куплено?
616. Решите уравнение:
1) (0,2* + 0,4х)-3,5 = 6,3; 3) {х—0,2х):0,4 = 1,6;
2) (0,7х — 0,2jc) • 6,4 = 9,6; 4) (0,4* +дс): 0,7 = 1,6.
Щ 617. Выполните деление:
а) -Н-; в) JJJ:д) 8:-f-; ж) 2f:lii;„) 2А:7§;
б>-Иг: г) §1:9; е) 7:3; а) 3 f: 1 |i ; к) 2 12 f.
618. Найдите значение выражения:
a) 7j-:4f.8;6) 11^:4};») lf'2f:lf; г) .
619. Выполните действия:
97
а> т:т+ т-т-1:1т-
4 Зак. 607
е) ((i j-j'-f)^.
620. Решите уравнение:
а) (*_8)~§—2; б) 2 2 ^=2 -1-.
621. Сколько оборотов сделает колесо на расстоянии 48 м,
б з 4 о
если длина окружности колеса равна — м; — м; —- м?
Zo 4 5
2 2
622. За —- ч мотоциклист проехал 20 — км. С какой ско-
3 5
ростью ехал мотоциклист?
623. На изготовлейие 16 одинаковых деталей требуется
п
6 — ч. Сколько времени занимает изготовление одной детали?
О
624. В двух сосудах 35 л жидкости. Известно, что в одном
сосуде жидкости в 1-^- раза меньше, чем в другом. Сколько
з
жидкости в каждом сосуде?
625. В двух пачках 156 тетрадей. Число тетрадей в одной
с
пачке составляет — числа тетрадей другой пачки. Сколько
тетрадей в каждой пачке?
626. Стоимость зимнего пальто на 84 р. больше стоимости летнего пальто. Сколько стоит каждое пальто, если стоимость летнего пальто составляет 60% стоимости зимнего?
627. Два катера движутся навстречу друг другу. Сейчас
7
между ними 25 км. Скорость одного из них составляет — ско-
о
г
рости другого. Найдите скорость каждого катера, если известно, что они встретятся через ч.
628. Турист ехал на автобусе 1 4- ч и на поезде 4-^- ч.
о 15
Всего этими видами транспорта турист проехал 456 км. При
g
этом на автобусе он проехал — того пути, который он проехал
на поезде. С какой скоростью турист ехал на автобусе и с какой — на поезде?
629. Выполните деление и округлите ответ до тысячных: а) 1,765:1,3; б) 5,394:23; в) 2,6:11,2.
630. Вычислите:
а) 74:100-0,4:10 + 17,8:1000;
б) 0,35 • 10 + 0,0237 • 100 - 0,00087 1000;
в) 37-0,01-0,2-0,1 + 8,9-Х),001;
г) 0,7:0,1 + 0,0474:0,01 — 0,00174:0,001.
Н.Я.Виленкин, А.С. Чесноков, С.И. Шварцбурд, В.И.Жохов, Математика для 6 класса, Учебник для средней школы
Планирование уроков по математике онлайн, задачи и ответы по классам, домашнее задание по математике 6 класса скачать
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|










