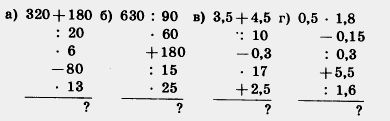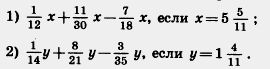|
|
|
| Строка 33: |
Строка 33: |
| | 867. Найдите площадь [[Image:21-07-169.jpg]] круга, у которого радиус 8 см. Найдите площадь второго круга, у которого радиус составляет [[Image:21-07-169.jpg]] радиуса первого круга. | | 867. Найдите площадь [[Image:21-07-169.jpg]] круга, у которого радиус 8 см. Найдите площадь второго круга, у которого радиус составляет [[Image:21-07-169.jpg]] радиуса первого круга. |
| | | | |
| - | 868. Решите задачу:<br>1) В -двух строительных бригадах 88 человек. В первой бригаде в 2 [[Image:21-07-170.jpg]] раза меньше людей, чем во второй. Сколько человек в каждой бригаде? | + | 868. Решите задачу:<br>1) В -двух строительных бригадах 88 человек. В первой бригаде в 2[[Image:21-07-171.jpg]] раза меньше людей, чем во второй. Сколько человек в каждой бригаде? |
| | | | |
| | 2) На двух животноводческих фермах работают 26 человек. | | 2) На двух животноводческих фермах работают 26 человек. |
| | | | |
| - | На первой ферме работают в 1 -4- раза больше людей, чем на<br>b<br>второй. Сколько человек работают на каждой ферме?<br>869. Найдите значение выражения:<br>г) Т2*+М*-Т8 если *=5ТГ; 2) ъУ+^У—кУ'*0™ У=1-П'<br>®<br> 870. Длина экватора Луны примерно равна 10,9 тыс. км. Чему равен диаметр Луны? (Результат округлите до сотен километров.) <br>871. Длина окружности 3,5 дм. Чему равна длина второй окружности, у которой диаметр составляет — диаметра первой окружности?<br>872. Найдите площадь круга, у которого диаметр равен 12 см. Найдите площадь круга, у которого диаметр в 2 раза меньше диаметра первого круга.<br>873. Для перевозки картофеля выделили две автомашины. На первую машину погрузили в 1,2 раза больше картофеля, чем на вторую. Сколько тонн картофеля погрузили на каждую автомашину, если на вторую погрузили на 0,9 т меньше, чем на первую?<br>874. Найдите значение выражения:<br>а) 150,88: (3,2 • 2,3) - 60,27: (4,1 • 1,4);<br>б) 592,92:(2,7 • 7,2) -102,48:(6,1 1,6).<br>Н Слово «пропорция» (от латинского proportio) означает «соразмерность», «определенное соотношение частей между собой».<br>Учение об отношениях и пропорциях особенно успешно развивалось в IV в. до н. э. в Древней Греции, славившейся произведениями искусства, архитектуры, развитыми ремеслами. С пропорциями связывались представления о красоте, порядке и гармонии, о созвучных аккордах в музыке. Теория отношений и пропорций была подробно изложена в «Началах» Евклида (III в. до н. э.), там, в частности, приводится и доказательство основного свойства пропорции.<br>С глубокой древности люди пользовались различными рычагами. Весло, лом, весы, ножницы, качели, тачка и т. д.— примеры рычагов. Выигрыш, который дает рычаг в прилагаемом<br> <br> <br><br>M L<br>усилии, определяется пропорцией —=—, где Мит — массы<br>т I<br>грузов, a L и I — «плечи» рычага.<br> <br>Рис. 47<br>Пропорциональность в природе, искусстве, архитектуре означает соблюдение определенных соотношений между размерами отдельных частей растения, скульптуры, здания и является непременным условием правильного и красивого изображения предмета.<br>Золотым сечением и даже «божественной пропорцией» называли математики древности и средневековья деление отрезка, при котором длина всего отрезка так относится к длине его большей части, как длина большей части к меньшей. На рисунке 47 точка С делит отрезок АВ в отношении золотого сечения.<br>Это отношение приближенно равно 0,618» — . Золотое сечение<br>о<br>чаще всёго применяется в произведениях искусства, архитектуре, встречается в природе.<br>На рисунке изображена знаменитая скульптура Аполлона Бельведерского, разделенная в таком отношении (точка С делит отрезок AD, точка В делит отрезок АС).<br>Красивейшее произведение древнегреческой архитектуры — Парфенон — построено в V в. до н. э. Отношение высоты здания к его длине равно 0,618.<br> <br> <br> <br>Окружающие нас предметы также часто дают примеры золотого сечения. Например, переплеты многих книг имеют отношение ширины и длины, близкое к- числу 0,618.<br>Рассматривая расположение листьев на общем стебле растений, можно заметить, чтр между каждыми двумя парами листьев (А и С) третья расположена в месте золотого сечения (точка В). <br><br><br><br><br> | + | На первой ферме работают в 1[[Image:21-07-170.jpg]] раза больше людей, чем на второй. Сколько человек работают на каждой ферме?<br>869. Найдите значение выражения:<br> |
| | + | |
| | + | [[Image:21-07-172.jpg]]<br><br> '''Д ''' 870. Длина экватора Луны примерно равна 10,9 тыс. км. Чему равен диаметр Луны? (Результат округлите до сотен километров.) <br> |
| | + | |
| | + | 871. Длина окружности 3,5 дм. Чему равна длина второй окружности, у которой диаметр составляет [[Image:21-07-173.jpg]] диаметра первой окружности?<br> |
| | + | |
| | + | 872. Найдите площадь круга, у которого диаметр равен 12 см. Найдите площадь круга, у которого диаметр в 2 раза меньше диаметра первого круга.<br> |
| | + | |
| | + | 873. Для перевозки картофеля выделили две автомашины. На первую машину погрузили в 1,2 раза больше картофеля, чем на вторую. Сколько тонн картофеля погрузили на каждую автомашину, если на вторую погрузили на 0,9 т меньше, чем на первую?<br> |
| | + | |
| | + | 874. Найдите значение выражения:<br> |
| | + | |
| | + | а) 150,88: (3,2 • 2,3) - 60,27: (4,1 • 1,4);<br>б) 592,92:(2,7 • 7,2) -102,48:(6,1 1,6).<br> |
| | + | |
| | + | '''А''' Слово «пропорция» (от латинского proportio) означает «соразмерность», «определенное соотношение частей между собой».<br> |
| | + | |
| | + | Учение об отношениях и пропорциях особенно успешно развивалось в IV в. до н. э. в Древней Греции, славившейся произведениями искусства, архитектуры, развитыми ремеслами. С пропорциями связывались представления о красоте, порядке и гармонии, о созвучных аккордах в музыке. Теория отношений и пропорций была подробно изложена в «Началах» Евклида (III в. до н. э.), там, в частности, приводится и доказательство основного свойства пропорции.<br> |
| | + | |
| | + | С глубокой древности люди пользовались различными рычагами. Весло, лом, весы, ножницы, качели, тачка и т. д.— примеры рычагов. Выигрыш, который дает рычаг в прилагаемом<br> <br>[[Image:21-07-174.jpg]] <br> |
| | + | |
| | + | <br>усилии, определяется пропорцией [[Image:21-07-175.jpg]], где ''М'' и ''m'' — массы грузов, a ''L'' и''I'' — «плечи» рычага.<br> |
| | + | |
| | + | Пропорциональность в природе, искусстве, архитектуре означает соблюдение определенных соотношений между размерами отдельных частей растения, скульптуры, здания и является непременным условием правильного и красивого изображения предмета.<br> |
| | + | |
| | + | [[Image:21-07-176.jpg]]<br> |
| | + | |
| | + | Золотым сечением и даже «божественной пропорцией» называли математики древности и средневековья деление отрезка, при котором длина всего отрезка так относится к длине его большей части, как длина большей части к меньшей. На рисунке 47 точка С делит отрезок АВ в отношении золотого сечения.<br>Это отношение приближенно равно [[Image:21-07-177.jpg]] . Золотое сечение чаще всёго применяется в произведениях искусства, архитектуре, встречается в природе.<br> |
| | + | |
| | + | На рисунке изображена знаменитая скульптура Аполлона Бельведерского, разделенная в таком отношении (точка С делит отрезок AD, точка В делит отрезок АС).<br>Красивейшее произведение древнегреческой архитектуры — Парфенон — построено в V в. до н. э. Отношение высоты здания к его длине равно 0,618.<br> <br> [[Image:21-07-178.jpg]] |
| | + | |
| | + | |
| | + | |
| | + | [[Image:21-07-179.jpg]]<br> <br>Окружающие нас предметы также часто дают примеры золотого сечения. Например, переплеты многих книг имеют отношение ширины и длины, близкое к числу 0,618. |
| | + | |
| | + | Рассматривая расположение листьев на общем стебле растений, можно заметить, чтр между каждыми двумя парами листьев (А и С) третья расположена в месте золотого сечения (точка В). <br><br><br><br><br> |
| | | | |
| | <br> ''Н.Я.Виленкин, А.С. Чесноков, С.И. Шварцбурд, В.И.Жохов, Математика для 6 класса, Учебник для средней школы'' <br> | | <br> ''Н.Я.Виленкин, А.С. Чесноков, С.И. Шварцбурд, В.И.Жохов, Математика для 6 класса, Учебник для средней школы'' <br> |
Версия 11:24, 21 июля 2010
Гипермаркет знаний>>Математика>>Математика 6 класс>>Математика: Шар-6 класс
25. Шар
Футбольный мяч, глобус, арбуз дают нам представление о шаре. Все точки поверхности шара одинаково удалены от центра шара. Отрезок, соединяющий точку поверхности шара с центром, называют радиусом шара. Отрезок, соединяющий две точки поверхности шара и проходящий через центр шара, называют диаметром шара. Диаметр шара равен двум радиусам. Поверхность шара называют сферой.
? Что называется радиусом шара? диаметром шара? Что такое сфера?
К 858. Диаметр земного шара приближенно равен 12,7 тыс. км. Скольким тысячам километров равен радиус и длина экватора Земли? (Число тысяч округлите до десятых.)
859. Один из самых больших глобусов Земли был изготовлен в 1889 г. для Парижской всемирной выставки. Его диаметр был 12,7 м. В каком масштабе этот глобус изображал Землю? Какова длина экватора и меридианов на этом глобусе?
860. Площадь поверхности Луны приближенно равна 38 млн. км2, что составляет 0,075 площади поверхности Земли. Найдите площадь поверхности Земли. (Результат округлите до миллионов квадратных километров.)
861. Диаметр планеты Меркурий приближенно равен 5 тыс. км. Диаметр планеты Венера в 2,48 раз больше, а диаметр планеты Марс составляет 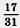 диаметра планеты Венера. Найдите диаметр планеты Венера и планеты Марс. диаметра планеты Венера. Найдите диаметр планеты Венера и планеты Марс.
П 862. Вычислите устно:
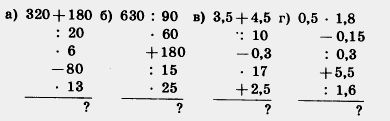
863. Масштаб плана 1:1000. На плане изображен круглый бассейн. Определите диаметр бассейна и его площадь, если на плане радиус бассейна 1 см.
864. Заполните таблицу:
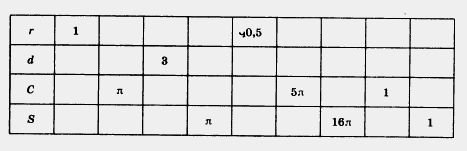
М 865. Цифры 1, 2, 3, 4, 5, 6, 7, 8, 9 расставьте в клетки так, чтобы равенства были верными:

866. Длина окружности 1,2 м. Чему равна длина другой окружности, у которой диаметр в 2 раза больше диаметра первой окружности?
867. Найдите площадь 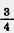 круга, у которого радиус 8 см. Найдите площадь второго круга, у которого радиус составляет круга, у которого радиус 8 см. Найдите площадь второго круга, у которого радиус составляет 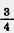 радиуса первого круга. радиуса первого круга.
868. Решите задачу:
1) В -двух строительных бригадах 88 человек. В первой бригаде в 2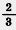 раза меньше людей, чем во второй. Сколько человек в каждой бригаде? раза меньше людей, чем во второй. Сколько человек в каждой бригаде?
2) На двух животноводческих фермах работают 26 человек.
На первой ферме работают в 1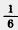 раза больше людей, чем на второй. Сколько человек работают на каждой ферме? раза больше людей, чем на второй. Сколько человек работают на каждой ферме?
869. Найдите значение выражения:
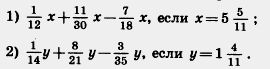
Д 870. Длина экватора Луны примерно равна 10,9 тыс. км. Чему равен диаметр Луны? (Результат округлите до сотен километров.)
871. Длина окружности 3,5 дм. Чему равна длина второй окружности, у которой диаметр составляет 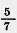 диаметра первой окружности? диаметра первой окружности?
872. Найдите площадь круга, у которого диаметр равен 12 см. Найдите площадь круга, у которого диаметр в 2 раза меньше диаметра первого круга.
873. Для перевозки картофеля выделили две автомашины. На первую машину погрузили в 1,2 раза больше картофеля, чем на вторую. Сколько тонн картофеля погрузили на каждую автомашину, если на вторую погрузили на 0,9 т меньше, чем на первую?
874. Найдите значение выражения:
а) 150,88: (3,2 • 2,3) - 60,27: (4,1 • 1,4);
б) 592,92:(2,7 • 7,2) -102,48:(6,1 1,6).
А Слово «пропорция» (от латинского proportio) означает «соразмерность», «определенное соотношение частей между собой».
Учение об отношениях и пропорциях особенно успешно развивалось в IV в. до н. э. в Древней Греции, славившейся произведениями искусства, архитектуры, развитыми ремеслами. С пропорциями связывались представления о красоте, порядке и гармонии, о созвучных аккордах в музыке. Теория отношений и пропорций была подробно изложена в «Началах» Евклида (III в. до н. э.), там, в частности, приводится и доказательство основного свойства пропорции.
С глубокой древности люди пользовались различными рычагами. Весло, лом, весы, ножницы, качели, тачка и т. д.— примеры рычагов. Выигрыш, который дает рычаг в прилагаемом
усилии, определяется пропорцией 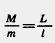 , где М и m — массы грузов, a L иI — «плечи» рычага. , где М и m — массы грузов, a L иI — «плечи» рычага.
Пропорциональность в природе, искусстве, архитектуре означает соблюдение определенных соотношений между размерами отдельных частей растения, скульптуры, здания и является непременным условием правильного и красивого изображения предмета.
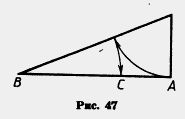
Золотым сечением и даже «божественной пропорцией» называли математики древности и средневековья деление отрезка, при котором длина всего отрезка так относится к длине его большей части, как длина большей части к меньшей. На рисунке 47 точка С делит отрезок АВ в отношении золотого сечения.
Это отношение приближенно равно  . Золотое сечение чаще всёго применяется в произведениях искусства, архитектуре, встречается в природе. . Золотое сечение чаще всёго применяется в произведениях искусства, архитектуре, встречается в природе.
На рисунке изображена знаменитая скульптура Аполлона Бельведерского, разделенная в таком отношении (точка С делит отрезок AD, точка В делит отрезок АС).
Красивейшее произведение древнегреческой архитектуры — Парфенон — построено в V в. до н. э. Отношение высоты здания к его длине равно 0,618.

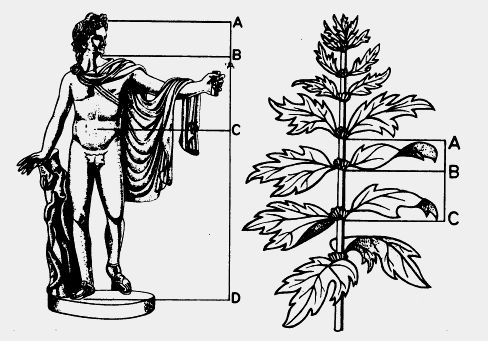
Окружающие нас предметы также часто дают примеры золотого сечения. Например, переплеты многих книг имеют отношение ширины и длины, близкое к числу 0,618.
Рассматривая расположение листьев на общем стебле растений, можно заметить, чтр между каждыми двумя парами листьев (А и С) третья расположена в месте золотого сечения (точка В).
Н.Я.Виленкин, А.С. Чесноков, С.И. Шварцбурд, В.И.Жохов, Математика для 6 класса, Учебник для средней школы
Математика для 6 класса, учебники и книги по математике скачать, библиотека онлайн
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|