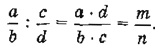|
|
|
| Строка 54: |
Строка 54: |
| | ''Обмен значениями двух переменных'' | | ''Обмен значениями двух переменных'' |
| | | | |
| - | Рассмотрим еще один очень полезный алгоритм, с которым при программировании часто приходится встречаться. Даны две переменные величины X и Y. Требуется произвести между ними обмен значениями. Например, если первоначально было:X= 1; Y = 2, то после обмена должно стать:X = 2, Y = 1. | + | Рассмотрим еще один очень полезный алгоритм, с которым при программировании часто приходится встречаться. Даны две переменные величины X и Y. Требуется произвести между ними обмен значениями. Например, если первоначально было: X= 1; Y = 2, то после обмена должно стать: X = 2, Y = 1. |
| | | | |
| | Хорошим аналогом для решения такой задачи является следующая: даны два стакана, в первом — молоко, во втором — вода; требуется произвести обмен их содержимым. Всякому ясно, что в этом случае нужен дополнительный третий пустой стакан. Последовательность действий будет следующей: | | Хорошим аналогом для решения такой задачи является следующая: даны два стакана, в первом — молоко, во втором — вода; требуется произвести обмен их содержимым. Всякому ясно, что в этом случае нужен дополнительный третий пустой стакан. Последовательность действий будет следующей: |
| Строка 109: |
Строка 109: |
| | 1. Числитель первой дроби умножить на знаменатель второй.<br>2. Знаменатель первой дроби умножить на числитель второй.<br>3. Записать дробь, числителем которой является результат выполнения пункта 1, а знаменателем — результат выполнения пункта 2. | | 1. Числитель первой дроби умножить на знаменатель второй.<br>2. Знаменатель первой дроби умножить на числитель второй.<br>3. Записать дробь, числителем которой является результат выполнения пункта 1, а знаменателем — результат выполнения пункта 2. |
| | | | |
| - | В алгебраической форме это выглядит следующим образом: | + | В алгебраической форме это выглядит следующим образом: |
| | | | |
| - | [[Image:Informatika_9_198.jpg]] | + | [[Image:Informatika 9 198.jpg]] |
| | | | |
| | Теперь построим алгоритм деления дробей для компьютера. В этом алгоритме сохраним те же обозначения для переменных, которые использованы в записанной выше формуле. Исходными данными являются целочисленные переменные а, b, с, d. Результатом — также целые величины m и n. | | Теперь построим алгоритм деления дробей для компьютера. В этом алгоритме сохраним те же обозначения для переменных, которые использованы в записанной выше формуле. Исходными данными являются целочисленные переменные а, b, с, d. Результатом — также целые величины m и n. |
| Строка 119: |
Строка 119: |
| | Раньше прямоугольник в схемах алгоритмов управления мы называли блоком простой команды. Для вычислительных алгоритмов такой простой командой является команда присваивания. Прямоугольник будем называть блоком присваивания, или вычислительным блоком. В форме параллелограмма рисуется блок ввода/вывода. Полученный алгоритм имеет линейную структуру (рис. 6.1). | | Раньше прямоугольник в схемах алгоритмов управления мы называли блоком простой команды. Для вычислительных алгоритмов такой простой командой является команда присваивания. Прямоугольник будем называть блоком присваивания, или вычислительным блоком. В форме параллелограмма рисуется блок ввода/вывода. Полученный алгоритм имеет линейную структуру (рис. 6.1). |
| | | | |
| - | [[Image:Informatika_9_199.jpg]] | + | [[Image:Informatika 9 199.jpg]] |
| | | | |
| | В алгоритме на АЯ строка, стоящая после заголовка алгоритма, называется описанием переменных. Служебное слово цел означает целый тип. Величины этого типа могут иметь только целочисленные значения. Описание переменных имеет вид: | | В алгоритме на АЯ строка, стоящая после заголовка алгоритма, называется описанием переменных. Служебное слово цел означает целый тип. Величины этого типа могут иметь только целочисленные значения. Описание переменных имеет вид: |
| Строка 155: |
Строка 155: |
| | Постарайтесь использовать минимальное количество дополнительных переменных. Выполните трассировку алгоритмов.<br>9. Запишите алгоритм циклического обмена значениями трех переменных А, В, С. Схема циклического обмена: | | Постарайтесь использовать минимальное количество дополнительных переменных. Выполните трассировку алгоритмов.<br>9. Запишите алгоритм циклического обмена значениями трех переменных А, В, С. Схема циклического обмена: |
| | | | |
| - | [[Image:Informatika_9_200.jpg]]<br> | + | [[Image:Informatika 9 200.jpg]]<br> |
| | | | |
| | Например, если до обмена было: А = 1, В = 2, С = 3, то после обмена должно стать: А = 3, В = 1, С=2. Выполните трассировку. | | Например, если до обмена было: А = 1, В = 2, С = 3, то после обмена должно стать: А = 3, В = 1, С=2. Выполните трассировку. |
Версия 16:13, 22 июля 2010
Гипермаркет знаний>>Информатика>>Информатика 9 класс>>Информатика: Линейные вычислительные алгоритмы
ЛИНЕЙНЫЕ ВЫЧИСЛИТЕЛЬНЫЕ АЛГОРИТМЫ
§ 34. Линейные вычислительные алгоритмы
Основные темы параграфа:
♦ присваивание; свойства присваивания;
♦ обмен значениями двух переменных;
♦ описание линейного вычислительного алгоритма.
Присваивание; свойства присваивания
Поскольку присваивание является важнейшей операцией в алгоритмах, работающих с величинами, то поговорим о ней более подробно.
Переменная величина получает значение в результате присваивания.
Присваивание производится компьютером при выполнении одной из двух команд из представленной выше системы: команды присваивания или команды ввода.
Рассмотрим последовательность выполнения четырех команд присваивания, в которых участвуют две переменные а и b. В приведенной ниже таблице против каждой команды указываются значения переменных, которые устанавливаются после ее выполнения. Такая таблица называется трассировочной таблицей, а процесс ее заполнения называется трассировкой алгоритма. Компьютер выполняет команды в порядке их записи в алгоритме.
Команда
| a
| b
|
a:= 1
| 1
| —
|
b:= 2 x a
| 1
| 2
|
a:= b
| 2
| 2
|
b:= a + b
| 2
| 4
|
Прочерк в таблице обозначает неопределенное значение переменной. Конечные значения, которые получают переменные а и b, соответственно равны 2 и 4.
Этот пример иллюстрирует три основных свойства присваивания. Вот эти свойства:
1) пока переменной не присвоена значения, она остается неопределенной;
2) значение, присвоенное переменной, сохраняется вплоть до выполнения следующего присваивания этой переменной нового значения;
3) новое значение, присвоенное переменной, заменяет ее предыдущее значение.
Обмен значениями двух переменных
Рассмотрим еще один очень полезный алгоритм, с которым при программировании часто приходится встречаться. Даны две переменные величины X и Y. Требуется произвести между ними обмен значениями. Например, если первоначально было: X= 1; Y = 2, то после обмена должно стать: X = 2, Y = 1.
Хорошим аналогом для решения такой задачи является следующая: даны два стакана, в первом — молоко, во втором — вода; требуется произвести обмен их содержимым. Всякому ясно, что в этом случае нужен дополнительный третий пустой стакан. Последовательность действий будет следующей:
1) перелить из 1-го в 3-й;
2) перелить из 2-го в 1-й;
3) перелить из 3-го во 2-й.
Цель достигнута!
По аналогии для обмена значениями двух переменных нужна третья дополнительная переменная, Назовем ее Z. Тогда задача решается последовательным выполнением трех операторов присваивания (пусть начальные значения 1 и 2 для переменных X и Y задаются вводом):
| Команда
| X
| Y
| Z
|
| ввод X, Y
| 1
| 2
| -
|
| Z:=X
| 1
| 2
| 1
|
| X:=Y
| 2
| 2
| 1
|
| Y:=Z
| 2
| 1
| 1
|
| вывод X, Y
| 2
| 1
| 1
|
Действительно, в итоге переменные X и Y поменялись значениями. На экран будут выведены значения X и Y в таком порядке: 2, 1. В трассировочной таблице выводимые значения выделены жирным шрифтом.
Аналогия со стаканами не совсем точна в том смысле, что при переливании из одного стакана в другой первый становится пустым. В результате же присваивания (Х:=Y) переменная, стоящая справа (Y), сохраняет свое значение.
Описание линейного вычислительного алгоритма
И наконец, рассмотрим пример составления алгоритма для решения следующей математической задачи: даны две простые дроби; получить дробь, являющуюся результатов их деления.
В школьном учебнике математики правила деления обыкновенных дробей описаны так:
1. Числитель первой дроби умножить на знаменатель второй.
2. Знаменатель первой дроби умножить на числитель второй.
3. Записать дробь, числителем которой является результат выполнения пункта 1, а знаменателем — результат выполнения пункта 2.
В алгебраической форме это выглядит следующим образом:
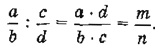
Теперь построим алгоритм деления дробей для компьютера. В этом алгоритме сохраним те же обозначения для переменных, которые использованы в записанной выше формуле. Исходными данными являются целочисленные переменные а, b, с, d. Результатом — также целые величины m и n.
Ниже алгоритм представлен в двух формах; в виде блок-схемы и на Алгоритмическом языке (АЯ).
Раньше прямоугольник в схемах алгоритмов управления мы называли блоком простой команды. Для вычислительных алгоритмов такой простой командой является команда присваивания. Прямоугольник будем называть блоком присваивания, или вычислительным блоком. В форме параллелограмма рисуется блок ввода/вывода. Полученный алгоритм имеет линейную структуру (рис. 6.1).
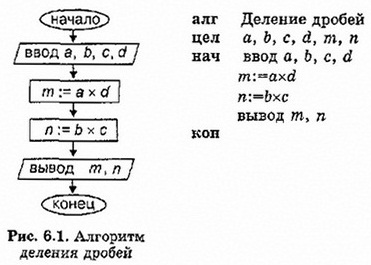
В алгоритме на АЯ строка, стоящая после заголовка алгоритма, называется описанием переменных. Служебное слово цел означает целый тип. Величины этого типа могут иметь только целочисленные значения. Описание переменных имеет вид:
<тип переменных> <список переменных>
Список переменных включает все переменные величины данного типа, входящие в алгоритм.
В блок-схемах типы переменных не указываются, но подразумеваются. Запись алгоритма на АЯ ближе по форме к языкам программирования, чем блок-схемы.
Коротко о главном
Основные свойства присваивания:
• значение переменной не определено, если ей не присвоено никакого значения;
• новое значение, присваиваемое переменной, заменяет ее старое значение;
• присвоенное переменной значение сохраняется в ней вплоть до нового присваивания.
Обмен значениями двух переменных производится через третью дополнительную переменную.
Трассировочная таблица используется для «ручного» исполнения алгоритма с целью его проверки.
В алгоритмах на АЯ указываются типы всех переменных. Такое указание называется описанием переменных.
Числовые величины, принимающие только целочисленные значения, описываются с помощью служебного слова цел (целый).
Вопросы и задания
1. Из каких команд составляется линейный вычислительный алгоритм?
2. Что такое трассировка? Как она производится?
3. В каком случае значение переменной считается неопределенным?
4. Что происходит с предыдущим значением переменной после присваивания ей нового значения?
5. Как вы думаете, можно ли использовать в арифметическом выражении оператора присваивания неопределенную переменную? К каким последствиям это может привести?
6. Напишите на АЯ алгоритм сложения двух простых дробей (без сокращения дроби).
7. Напишите на АЯ алгоритм вычисления у по формуле
у = (1 - х2 + 5х4)2,
где х — заданное целое число. Учтите следующие ограничения:
1) в арифметических выражениях можно использовать только операций сложения, вычитания и умножений; 2) выражение может содержать только одну арифметическую операцию. Выполните трассировку алгоритма при х = 2.
8. Пользуясь ограничениями предыдущей задачи, напишите наиболее короткие алгоритмы вычисления выражений:
y = х8; y = x10; y = х15; у = х19.
Постарайтесь использовать минимальное количество дополнительных переменных. Выполните трассировку алгоритмов.
9. Запишите алгоритм циклического обмена значениями трех переменных А, В, С. Схема циклического обмена:
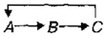
Например, если до обмена было: А = 1, В = 2, С = 3, то после обмена должно стать: А = 3, В = 1, С=2. Выполните трассировку.
И. Семакин, Л. Залогова, С. Русаков, Л. Шестакова, Информатика, 9 класс
Отослано читателями из интернет-сайтов
Основы информатики, подборка рефератов к урокам информатики, скачать рефераты, уроки информатики 9 класс онлайн, домашняя работа
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|