|
|
|
| Строка 68: |
Строка 68: |
| | На рис. 6.8 приведена блок-схема алгоритма Евклида. | | На рис. 6.8 приведена блок-схема алгоритма Евклида. |
| | | | |
| - | [[Image:Informatika 9 231.jpg]] | + | [[Image:Informatika_9_231_1.jpg]]<br> |
| | | | |
| | Структура алгоритма — цикл-пока с вложенным ветвлением. Цикл повторяется, пока значения М и N не равны друг другу. В ветвлении большее из двух значений заменяется на их разность. | | Структура алгоритма — цикл-пока с вложенным ветвлением. Цикл повторяется, пока значения М и N не равны друг другу. В ветвлении большее из двух значений заменяется на их разность. |
| Строка 169: |
Строка 169: |
| | В итоге получился верный результат. | | В итоге получился верный результат. |
| | | | |
| - | ''Программа на АЯ и на Паскале'' | + | ''Программа на АЯ и на Паскале'' |
| | | | |
| | Запишем алгоритм на АЯ и программу на Паскале. | | Запишем алгоритм на АЯ и программу на Паскале. |
| | | | |
| - | [[Image:Informatika_9_232.jpg]] | + | [[Image:Informatika_9_232_1.jpg]]<br> |
| | | | |
| - | <u>''Коротко о главном''</u> | + | <u>''Коротко о главном''</u> |
| | | | |
| - | Алгоритм Евклида предназначен для получения наибольшего общего делителя двух натуральных чисел. Структура алгоритма Евклида — цикл с вложенным ветвлением. | + | Алгоритм Евклида предназначен для получения наибольшего общего делителя двух натуральных чисел. Структура алгоритма Евклида — цикл с вложенным ветвлением. |
| | | | |
| - | Ручная трассировка может использоваться для проверки правильности лишь сравнительно простых алгоритмов. Правильность программ проверяется путем тестирования на компьютере. | + | Ручная трассировка может использоваться для проверки правильности лишь сравнительно простых алгоритмов. Правильность программ проверяется путем тестирования на компьютере. |
| | | | |
| - | <u>''Вопросы и задания''</u> | + | <u>''Вопросы и задания''</u> |
| | | | |
| | 1. Выполните на компьютере программу Еvklid. Протестируйте ее на значениях М= 32, N = 24; М = 696, N = 234.<br>2. Составьте программу нахождения наибольшего общего делителя трех чисел, используя следующую формулу:<br>НОД(А, B, С) = НОД(НОД(A, В), С).<br>3. Составьте программу нахождения наименьшего общего кратного (НОК) двух чисел, используя формулу:<br>А·В = НОД(А, В)·HOK(А, В).<br><br> ''И. Семакин, Л. Залогова, С. Русаков, Л. Шестакова, Информатика, 9 класс<br>Отослано читателями из интернет-сайтов'' | | 1. Выполните на компьютере программу Еvklid. Протестируйте ее на значениях М= 32, N = 24; М = 696, N = 234.<br>2. Составьте программу нахождения наибольшего общего делителя трех чисел, используя следующую формулу:<br>НОД(А, B, С) = НОД(НОД(A, В), С).<br>3. Составьте программу нахождения наименьшего общего кратного (НОК) двух чисел, используя формулу:<br>А·В = НОД(А, В)·HOK(А, В).<br><br> ''И. Семакин, Л. Залогова, С. Русаков, Л. Шестакова, Информатика, 9 класс<br>Отослано читателями из интернет-сайтов'' |
Версия 13:10, 29 июля 2010
Гипермаркет знаний>>Информатика>>Информатика 9 класс>>Информатика: Алгоритм Евклида
АЛГОРИТМ ЕВКЛИДА
§ 40. Алгоритм Евклида
Основные темы параграфа:
♦ наибольший общий делитель;
♦ идея алгоритма Евклида;
♦ описание алгоритма Евклида блок-схемой;
♦ программа на AЯ и на Паскале.
Наибольший общий делитель
Рассмотрим следующую задачу: требуется составить программу определения наибольшего общего делителя (НОД) двух натуральных чисел.
Вспомним математику. Наибольший общий делитель двух натуральных чисел — это самое большое натуральное число, на которое они делятся нацело. Например, у чисел 12 и 18 имеются общие делители: 2, 3, 6. Наибольшим общим делителем является число 6. Это записывается так:
НOД(12, 18) = 6.
Обозначим исходные данные как М и N. Постановка задачи выглядит следующим образом:
Дано: М, N
Найти: НОД(M, N).
В данном случае какой-то дополнительной математической формализации не требуется. Сама постановка задачи носит формальный математический характер. Не существует формулы для вычисления НОД(М, N) по значениям М и N. Но зато достаточно давно, задолго до появления ЭВМ, был известен алгоритмический способ решения этой задачи. Называется он алгоритмом Евклида.
Идея алгоритма Евклида
Идея этого алгоритма основана на том свойстве, что если М>N, то
НОД(М, N) = НОД(М – N, N).
Иначе говоря, НОД двух натуральных чисел равен НОД их положительной разности (модуля их разности) и меньшего числа.
Легко доказать это свойство. Пусть К — общий делитель М и N (М > Н). Это значит, что М = mК, N = nК, где m,n — натуральные числа, причем m > n. Тогда М - N = К(m - n), откуда следует, что К — делитель числа М - N. Значит, все общие делители чисел М и N являются делителями их разности М - N в том числе и наибольший общий делитель.
Второе очевидное свойство:
НОД(М, М) = М.
Для «ручного» счета алгоритм Евклида выглядит так:
1) если числа равны, то взять любое из них в качестве ответа, в противном случае продолжить выполнение алгоритма;
2) затенить большее число разностью большего и меньшего из чисел;
3) вернуться к выполнению п. 1.
Рассмотрим этот алгоритм на примере М=32, N=24:
Получили: НОД(32, 24) = НОД(8, 8) = 8, что верно.
Описание алгоритма Евклида блок-схемой
На рис. 6.8 приведена блок-схема алгоритма Евклида.
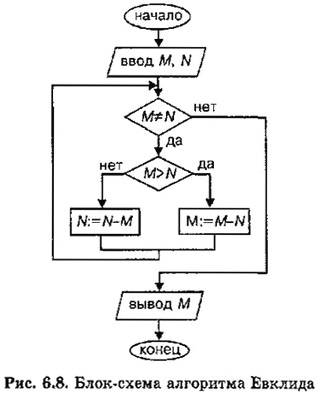
Структура алгоритма — цикл-пока с вложенным ветвлением. Цикл повторяется, пока значения М и N не равны друг другу. В ветвлении большее из двух значений заменяется на их разность.
А теперь посмотрите на трассировочную таблицу алгоритма для исходных значений М = 32, N = 24.
| Шаг
| Операция
| M
| N
| Условие
|
| 1
| ввод M
| 32
|
|
|
| 2
| ввод N
|
| 24
|
|
| 3
| M≠N
|
|
| 32≠24, да
|
| 4
| M>N
|
|
| 32>24, да
|
| 5
| M:=M-N
| 8
|
|
|
| 6
| M≠N
|
|
| 8≠24, да
|
| 7
| M>N
|
|
| 8>24, нет
|
| 8
| N:=N-M
|
| 16
|
|
| 9
| M≠N
|
|
| 8≠16, да
|
| 10
| M>N
|
|
| 8>16, нет
|
| 11
| N:=N-M
|
| 8
|
|
| 12
| M≠N
|
|
| 8≠8, нет
|
| 13
| вывод М
| 8
|
|
|
| 14
| конец
|
|
|
|
В итоге получился верный результат.
Программа на АЯ и на Паскале
Запишем алгоритм на АЯ и программу на Паскале.

Коротко о главном
Алгоритм Евклида предназначен для получения наибольшего общего делителя двух натуральных чисел. Структура алгоритма Евклида — цикл с вложенным ветвлением.
Ручная трассировка может использоваться для проверки правильности лишь сравнительно простых алгоритмов. Правильность программ проверяется путем тестирования на компьютере.
Вопросы и задания
1. Выполните на компьютере программу Еvklid. Протестируйте ее на значениях М= 32, N = 24; М = 696, N = 234.
2. Составьте программу нахождения наибольшего общего делителя трех чисел, используя следующую формулу:
НОД(А, B, С) = НОД(НОД(A, В), С).
3. Составьте программу нахождения наименьшего общего кратного (НОК) двух чисел, используя формулу:
А·В = НОД(А, В)·HOK(А, В).
И. Семакин, Л. Залогова, С. Русаков, Л. Шестакова, Информатика, 9 класс
Отослано читателями из интернет-сайтов
Вся информатика онлайн, список тем по предметам, сборник конспектов по информатике, домашняя работа, вопросы и ответы, рефераты по информатике 9 класс, планы уроков
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|












