|
|
|
| Строка 1: |
Строка 1: |
| - | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Информатика|Информатика]]>>[[Информатика 10 класс|Информатика 10 класс]]>>Информатика: Представление числовой информации с помощью систем счисления''' | + | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Информатика|Информатика]]>>[[Информатика 10 класс|Информатика 10 класс]]>>Информатика: Представление числовой информации с помощью систем счисления''' <metakeywords>Представление, числовой, информации, помощью, систем, счисления</metakeywords> <br> Для записи информации о количестве объектов используются числа. Числа записываются с использованием особых знаковых систем, которые называются системами счисления. Алфавит системы счисления состоит из символов, которые называются цифрами. |
| - | <metakeywords>Представление, числовой, информации, помощью, систем, счисления</metakeywords> | + | |
| - | <br> | + | '''Система счисления''' — это знаковая система, в которой числа записываются по определенным правилам с помощью символов некоторого алфавита, называемых цифрами. Все системы счисления делятся на две большие группы: позиционные и непозиционные. В позиционных системах счисления количественное значение цифры зависит от ее положения в числе, а в непозиционных — не зависит. |
| | + | |
| | + | '''Непозиционные системы счисления.''' Примером непозиционной системы, которая сохранилась до наших дней, может служить римская система счисления, которая начала применяться более двух с половиной тысяч лет назад в Древнем Риме. В основе римской системы счисления лежат знаки I (один палец) для числа 1, V (раскрытая ладонь) для числа 5, X (две сложенные ладони) для числа 10, а для обозначения чисел 50, 100, 500 и 1000 используются латинские буквы L, С, D и М. В римской системе счисления количественное значение цифры не зависит от ее положения в числе. Например, в римском числе XXX (30) цифра X встречается трижды и в каждом случае обозначает одну и ту же величину — число 10, три раза по 10 в сумме дают 30. |
| | + | |
| | + | '''Позиционные системы счисления.''' Каждая позиционная система счисления имеет определенный алфавит цифр и основание. Основание системы равно количеству цифр (знаков) в ее алфавите. В позиционных системах счисления количественное значение цифры зависит от ее позиции в числе. Позиция цифры в числе называется разрядом. Разряды числа возрастают справа налево, от младших разрядов к старшим. Основание показывает, во сколько раз изменяется значение цифры при перемещении ее в соседний разряд. В настоящее время наиболее распространенными позиционными системами счисления являются десятичная и двоичная. |
| | + | |
| | + | Десятичная система счисления имеет алфавит цифр, который состоит из десяти всем известных, так называемых арабских, цифр {0,1,2,3,4,5,6,7,8,9}, а двоичная — две цифры {0,1} (табл. 1.1). |
| | + | |
| | + | [[Image:информатика 10 24 1.jpeg]] |
| | + | |
| | + | Десятичная система счисления. В десятичной системе счисления цифра в крайней справа позиции обозначает единицы, цифра, смещенная на одну позицию влево, обозначает десятки, еще левее — сотни, затем — тысячи и т. д. |
| | + | |
| | + | Рассмотрим в качестве примера десятичное число 333. Цифра 3 встречается в числе трижды, причем самая правая обозначает три единицы, вторая справа — три десятка и, наконец, третья — три сотни. Выше десятичное число 333 было записано в привычной для нас свернутой форме. Мы настолько привыкли к такой форме записи, что уже не замечаем, как в уме умножаем цифры числа на различные степени числа 10, которое является основанием десятичной системы счисления. |
| | + | |
| | + | В '''развернутой форме записи числа''' умножение цифр числа на основание производится в явной форме. Так, в развернутой форме запись числа 333 в десятичной системе будет выглядеть следующим образом: 33310 - 3 • 102 + 3 • 101 + 3 • 100. Для записи десятичных дробей используются разряды с отрицательными значениями степеней основания. Например, число 333,33 в развернутой форме будет записываться следующим образом: |
| | + | |
| | + | 333,33<sub>10</sub> = 3 • 10<sup>2</sup> + 3 • 10<sup>1</sup> + 3 • 10<sup>0</sup>+ 3• 10<sup>-1</sup> + 3 • 10<sup>-2</sup>. |
| | + | |
| | + | Числа в позиционных системах счисления записываются '''в виде суммы числового ряда степеней''' основания, в качестве коэффициентов которых выступают цифры данного числа. Умножение или деление десятичного числа на 10 (величину основания) приводит к перемещению запятой, отделяющей |
| | + | |
| | + | целую часть от дробной, на один разряд вправо или влево. Например: |
| | + | |
| | + | 333,33<sub>10</sub> • 10 = 3333,3<sub>10</sub>, |
| | + | |
| | + | 333,33<sub>10</sub> • 10 = 33,333<sub>10</sub>. |
| | + | |
| | + | '''Двоичная система счисления.''' Числа в двоичной системе в развернутой форме записываются в виде суммы ряда степеней основания 2 с коэффициентами, в качестве которых выступают цифры 0 или 1. Например, развернутая запись двоичного числа выглядит следующим образом: |
| | + | |
| | + | А2 = 1 • 2<sup>2</sup> + 1 • 2<sup>1</sup> + 0 • 2<sup>0</sup> + 0 • 2<sup>-1</sup> + 1 • 2<sup>-2</sup>, а в свернутой форме: А<sub>2</sub> = 110,01<sub>2</sub>. Умножение или деление двоичного числа на 2 (величину основания) приводит к перемещению запятой, отделяющей целую часть от дробной на один разряд вправо или влево. Например: |
| | + | |
| | + | 110,01<sub>2</sub> • 2 = 1100,1<sub>2</sub>, |
| | + | |
| | + | 110,01<sub>2</sub> : 2 = 11,001<sub>2</sub>. |
| | + | |
| | + | '''Контрольные вопросы''' |
| | + | |
| | + | 1. Чем отличаются позиционные системы счисления от непозиционных? |
| | + | |
| | + | 2. Каково основание десятичной системы счисления? Двоичной системы счисления? |
| | + | |
| | + | 3. Какие цифры входят в алфавит десятичной системы счисления? Двоичиой системы счисления? |
| | + | |
| | + | 4. На какую величину в позиционных системах счисления различаются цифры соседних разрядов числа? |
| | | | |
| | <br> ''Информатика и ИКТ: Учебник для 10 кл. Н.Д. Угринович''<br> | | <br> ''Информатика и ИКТ: Учебник для 10 кл. Н.Д. Угринович''<br> |
| | | | |
| | + | <br> |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
Версия 04:52, 21 августа 2010
Гипермаркет знаний>>Информатика>>Информатика 10 класс>>Информатика: Представление числовой информации с помощью систем счисления
Для записи информации о количестве объектов используются числа. Числа записываются с использованием особых знаковых систем, которые называются системами счисления. Алфавит системы счисления состоит из символов, которые называются цифрами.
Система счисления — это знаковая система, в которой числа записываются по определенным правилам с помощью символов некоторого алфавита, называемых цифрами. Все системы счисления делятся на две большие группы: позиционные и непозиционные. В позиционных системах счисления количественное значение цифры зависит от ее положения в числе, а в непозиционных — не зависит.
Непозиционные системы счисления. Примером непозиционной системы, которая сохранилась до наших дней, может служить римская система счисления, которая начала применяться более двух с половиной тысяч лет назад в Древнем Риме. В основе римской системы счисления лежат знаки I (один палец) для числа 1, V (раскрытая ладонь) для числа 5, X (две сложенные ладони) для числа 10, а для обозначения чисел 50, 100, 500 и 1000 используются латинские буквы L, С, D и М. В римской системе счисления количественное значение цифры не зависит от ее положения в числе. Например, в римском числе XXX (30) цифра X встречается трижды и в каждом случае обозначает одну и ту же величину — число 10, три раза по 10 в сумме дают 30.
Позиционные системы счисления. Каждая позиционная система счисления имеет определенный алфавит цифр и основание. Основание системы равно количеству цифр (знаков) в ее алфавите. В позиционных системах счисления количественное значение цифры зависит от ее позиции в числе. Позиция цифры в числе называется разрядом. Разряды числа возрастают справа налево, от младших разрядов к старшим. Основание показывает, во сколько раз изменяется значение цифры при перемещении ее в соседний разряд. В настоящее время наиболее распространенными позиционными системами счисления являются десятичная и двоичная.
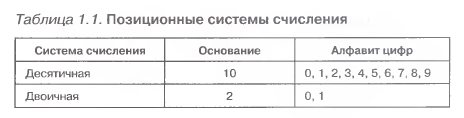
Десятичная система счисления имеет алфавит цифр, который состоит из десяти всем известных, так называемых арабских, цифр {0,1,2,3,4,5,6,7,8,9}, а двоичная — две цифры {0,1} (табл. 1.1).
Десятичная система счисления. В десятичной системе счисления цифра в крайней справа позиции обозначает единицы, цифра, смещенная на одну позицию влево, обозначает десятки, еще левее — сотни, затем — тысячи и т. д.
Рассмотрим в качестве примера десятичное число 333. Цифра 3 встречается в числе трижды, причем самая правая обозначает три единицы, вторая справа — три десятка и, наконец, третья — три сотни. Выше десятичное число 333 было записано в привычной для нас свернутой форме. Мы настолько привыкли к такой форме записи, что уже не замечаем, как в уме умножаем цифры числа на различные степени числа 10, которое является основанием десятичной системы счисления.
В развернутой форме записи числа умножение цифр числа на основание производится в явной форме. Так, в развернутой форме запись числа 333 в десятичной системе будет выглядеть следующим образом: 33310 - 3 • 102 + 3 • 101 + 3 • 100. Для записи десятичных дробей используются разряды с отрицательными значениями степеней основания. Например, число 333,33 в развернутой форме будет записываться следующим образом:
333,3310 = 3 • 102 + 3 • 101 + 3 • 100+ 3• 10-1 + 3 • 10-2.
Числа в позиционных системах счисления записываются в виде суммы числового ряда степеней основания, в качестве коэффициентов которых выступают цифры данного числа. Умножение или деление десятичного числа на 10 (величину основания) приводит к перемещению запятой, отделяющей
целую часть от дробной, на один разряд вправо или влево. Например:
333,3310 • 10 = 3333,310,
333,3310 • 10 = 33,33310.
Двоичная система счисления. Числа в двоичной системе в развернутой форме записываются в виде суммы ряда степеней основания 2 с коэффициентами, в качестве которых выступают цифры 0 или 1. Например, развернутая запись двоичного числа выглядит следующим образом:
А2 = 1 • 22 + 1 • 21 + 0 • 20 + 0 • 2-1 + 1 • 2-2, а в свернутой форме: А2 = 110,012. Умножение или деление двоичного числа на 2 (величину основания) приводит к перемещению запятой, отделяющей целую часть от дробной на один разряд вправо или влево. Например:
110,012 • 2 = 1100,12,
110,012 : 2 = 11,0012.
Контрольные вопросы
1. Чем отличаются позиционные системы счисления от непозиционных?
2. Каково основание десятичной системы счисления? Двоичной системы счисления?
3. Какие цифры входят в алфавит десятичной системы счисления? Двоичиой системы счисления?
4. На какую величину в позиционных системах счисления различаются цифры соседних разрядов числа?
Информатика и ИКТ: Учебник для 10 кл. Н.Д. Угринович
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|











