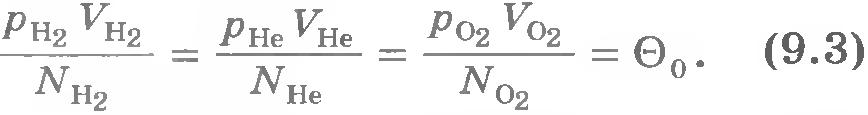|
|
|
| Строка 5: |
Строка 5: |
| | <metakeywords>Физика, 10 класс, Определение температуры</metakeywords> | | <metakeywords>Физика, 10 класс, Определение температуры</metakeywords> |
| | | | |
| - | При тепловом равновесии средняя кинетическая энергия поступательного движения молекул всех газов одинакова. В этом вы скоро убедитесь.<br> '''Средняя кинетическая энергия молекул газа при тепловом равновесии.''' Возьмем сосуд, разделенный пополам перегородкой, проводящей тепло. В одну половину сосуда поместим кислород, а в другую - водород, имеющие разную температуру. Спустя некоторое время газы будут иметь одинаковую температуру, не зависящую от рода газа, т. е. будут находиться в состоянии теплового равновесия. Для определения температуры выясним, какая физическая величина в молекулярно-кинетической теории обладает таким же свойством.<br> Из курса физики 7 класса известно, что, чем быстрее движутся молекулы, тем выше температура тела. При нагревании газа в замкнутом сосуде давление газа возрастает. Согласно же основному уравнению молекулярно-кинетической теории (8.15) давление газа ''p'' прямо пропорционально средней кинетической энергии поступательного движения молекул: [[Image:a65-8.jpg]]. При тепловом равновесии, если давление газа данной массы и его объем фиксированы, средняя кинетическая энергия молекул газа должна иметь строго определенное значение, как и температура.<br> Можно предположить, что ''при тепловом равновесии именно средние кинетические энергии молекул всех газов одинаковы''. Конечно, это пока только предположение. Его нужно экспериментально проверить. Практически такую проверку произвести непосредственно невозможно, так как измерить среднюю кинетическую энергию молекул очень трудно. Но с помощью основного уравнения молекулярно-кинетической теории ее можно выразить через макроскопические параметры.<br> Так как концентрация молекул газа [[Image:a65-9.jpg]], то из уравнения (8.15) получаем [[Image:a65-1.jpg]], или | + | При тепловом равновесии средняя кинетическая энергия поступательного движения молекул всех газов одинакова. В этом вы скоро убедитесь.<br> '''Средняя кинетическая энергия молекул газа при тепловом равновесии.''' Возьмем сосуд, разделенный пополам перегородкой, проводящей тепло. В одну половину сосуда поместим кислород, а в другую - водород, имеющие разную температуру. Спустя некоторое время газы будут иметь одинаковую температуру, не зависящую от рода газа, т. е. будут находиться в состоянии теплового равновесия. Для определения температуры выясним, какая физическая величина в молекулярно-кинетической теории обладает таким же свойством.<br> Из курса физики 7 класса известно, что, чем быстрее движутся молекулы, тем выше температура тела. При нагревании газа в замкнутом сосуде давление газа возрастает. Согласно же основному уравнению молекулярно-кинетической теории (8.15) давление газа ''p'' прямо пропорционально средней кинетической энергии поступательного движения молекул: [[Image:A65-8.jpg|83x37px]]. При тепловом равновесии, если давление газа данной массы и его объем фиксированы, средняя кинетическая энергия молекул газа должна иметь строго определенное значение, как и температура.<br> Можно предположить, что ''при тепловом равновесии именно средние кинетические энергии молекул всех газов одинаковы''. Конечно, это пока только предположение. Его нужно экспериментально проверить. Практически такую проверку произвести непосредственно невозможно, так как измерить среднюю кинетическую энергию молекул очень трудно. Но с помощью основного уравнения молекулярно-кинетической теории ее можно выразить через макроскопические параметры.<br> Так как концентрация молекул газа [[Image:A65-9.jpg|55x33px]], то из уравнения (8.15) получаем [[Image:A65-1.jpg|96x36px]], или |
| | | | |
| - | [[Image:a65-2.jpg|center]] Давление ''p'' и объем ''V'' измеряются непосредственно. Число молекул ''N'' можно определить, зная массу газа ''m'', постоянную Авогадро ''N<sub>A</sub>'' и молярную массу ''M''. Согласно формуле (8.8)<br>[[Image:a65-3.jpg|center]] Если кинетическая энергия [[Image:a63-18.jpg]] действительно одинакова для всех газов в состоянии теплового равновесия, то и величина ''p'' должна быть тоже одинаковой для всех газов. Только опыт может подтвердить или опровергнуть данное предположение.<br> '''Газы в состоянии теплового равновесия.''' Опыт можно осуществить так. Возьмем несколько сосудов, заполненных различными газами, например водородом, гелием и кислородом. Сосуды имеют определенные объемы и снабжены манометрами. Это позволяет измерить давление в каждом сосуде. Массы газов известны, тем самым известно число молекул в каждом сосуде.<br> Приведем газы в состояние теплового равновесия. Для этого поместим их в тающий лед и подождем, пока не установится тепловое равновесие и давление газов перестанет меняться (''рис.9.2''). После этого можно утверждать, что все газы имеют одинаковую температуру 0°С. Давления газов ''p'', их объемы ''V'' и число молекул ''N'' различны. Найдем отношение [[Image:a65-10.jpg]] для водорода. Если, к примеру, водород, количество вещества которого равно 1 моль, занимает объем ''V<sub>H2</sub>''=0,1 м<sup>3</sup>, то при температуре 0°С давление оказывается равным ''p<sub>H2</sub>''=2,265•10<sup>4</sup> Па. Отсюда<br>[[Image:a65-4.jpg|center]][[Image:a9.2.jpg|center]] Такое же значение отношения произведения давления газа на его объем к числу молекул получается и для всех других газов при температуре тающего льда. Обозначим это отношение через [[Image:a65-11.jpg]]. Тогда<br>[[Image:a65-5.jpg|center]] Таким образом, наше предположение оказалось верным.<br> Правда, соотношение (9.3) не является абсолютно точным. При давлениях в сотни атмосфер, когда газы становятся весьма плотными, отношение [[Image:a65-10.jpg]] перестает быть строго определенным, не зависящим от занимаемых газами объемов. ''Оно выполняется для газов, когда их можно считать идеальными.''<br> Если же сосуды с газами поместить в кипящую воду при нормальном атмосферном давлении, то упомянутое отношение по-прежнему будет одним и тем же для всех газов, но больше, чем предыдущее. Как показывает опыт,<br>[[Image:a65-7.jpg|center]] '''Определение температуры.''' Можно, следовательно, утверждать, что величина [[Image:a65-12.jpg]] растет с повышением температуры. Более того, [[Image:a65-12.jpg]] ни от чего, кроме температуры, не зависит. Ведь для идеальных газов [[Image:a65-12.jpg]] не зависит ни от рода газа, ни от его объема или давления, а также от числа частиц в сосуде и формы самого сосуда. Этот опытный факт позволяет рассматривать величину [[Image:a65-12.jpg]] как естественную меру температуры, определяемую через другие макроскопические параметры газа. В принципе можно было бы считать температурой и саму величину [[Image:a65-12.jpg]] и измерять температуру в энергетических единицах - джоулях. Однако, во-первых, это неудобно для практического использования (температуре 100°С соответствовала бы очень малая величина - порядка 10<sup>-21</sup> Дж), а во-вторых, и это главное, уже давно ''принято выражать температуру в градусах.''<br> Мы нашли способ получать значения температуры, не зависящие от свойств газов, которые при этом используются. Пока что температуру мы выразили в энергетических единицах.<br><br><br> ???<br> 1. На каком основании можно предполагать существование связи между температурой и кинетической энергией молекул?<br> 2. Как связаны объем, давление и число молекул различных газов в состоянии теплового равновесия?<br> | + | [[Image:A65-2.jpg|center|174x35px]] Давление ''p'' и объем ''V'' измеряются непосредственно. Число молекул ''N'' можно определить, зная массу газа ''m'', постоянную Авогадро ''N<sub>A</sub>'' и молярную массу ''M''. Согласно формуле (8.8)<br>[[Image:A65-3.jpg|center|105x34px]] Если кинетическая энергия [[Image:A63-18.jpg|17x20px]] действительно одинакова для всех газов в состоянии теплового равновесия, то и величина ''p'' должна быть тоже одинаковой для всех газов. Только опыт может подтвердить или опровергнуть данное предположение.<br> '''Газы в состоянии теплового равновесия.''' Опыт можно осуществить так. Возьмем несколько сосудов, заполненных различными газами, например водородом, гелием и кислородом. Сосуды имеют определенные объемы и снабжены манометрами. Это позволяет измерить давление в каждом сосуде. Массы газов известны, тем самым известно число молекул в каждом сосуде.<br> Приведем газы в состояние теплового равновесия. Для этого поместим их в тающий лед и подождем, пока не установится тепловое равновесие и давление газов перестанет меняться (''рис.9.2''). После этого можно утверждать, что все газы имеют одинаковую температуру 0°С. Давления газов ''p'', их объемы ''V'' и число молекул ''N'' различны. Найдем отношение [[Image:A65-10.jpg|30x43px]] для водорода. Если, к примеру, водород, количество вещества которого равно 1 моль, занимает объем ''V<sub>H2</sub>''=0,1 м<sup>3</sup>, то при температуре 0°С давление оказывается равным ''p<sub>H2</sub>''=2,265•10<sup>4</sup> Па. Отсюда<br>[[Image:A65-4.jpg|center|458x41px]][[Image:A9.2.jpg|center|445x153px]] Такое же значение отношения произведения давления газа на его объем к числу молекул получается и для всех других газов при температуре тающего льда. Обозначим это отношение через [[Image:A65-11.jpg|21x21px]]. Тогда<br>[[Image:A65-5.jpg|center|378x50px]] Таким образом, наше предположение оказалось верным.<br> Правда, соотношение (9.3) не является абсолютно точным. При давлениях в сотни атмосфер, когда газы становятся весьма плотными, отношение [[Image:A65-10.jpg|24x35px]] перестает быть строго определенным, не зависящим от занимаемых газами объемов. ''Оно выполняется для газов, когда их можно считать идеальными.''<br> Если же сосуды с газами поместить в кипящую воду при нормальном атмосферном давлении, то упомянутое отношение по-прежнему будет одним и тем же для всех газов, но больше, чем предыдущее. Как показывает опыт,<br>[[Image:A65-7.jpg|center|293x35px]] '''Определение температуры.''' Можно, следовательно, утверждать, что величина [[Image:A65-12.jpg|15x16px]] растет с повышением температуры. Более того, [[Image:A65-12.jpg|15x16px]] ни от чего, кроме температуры, не зависит. Ведь для идеальных газов [[Image:A65-12.jpg|17x18px]] не зависит ни от рода газа, ни от его объема или давления, а также от числа частиц в сосуде и формы самого сосуда. Этот опытный факт позволяет рассматривать величину [[Image:A65-12.jpg|15x16px]] как естественную меру температуры, определяемую через другие макроскопические параметры газа. В принципе можно было бы считать температурой и саму величину [[Image:A65-12.jpg|16x17px]] и измерять температуру в энергетических единицах - джоулях. Однако, во-первых, это неудобно для практического использования (температуре 100°С соответствовала бы очень малая величина - порядка 10<sup>-21</sup> Дж), а во-вторых, и это главное, уже давно ''принято выражать температуру в градусах.''<br> Мы нашли способ получать значения температуры, не зависящие от свойств газов, которые при этом используются. Пока что температуру мы выразили в энергетических единицах.<br><br><br> ???<br> 1. На каком основании можно предполагать существование связи между температурой и кинетической энергией молекул?<br> 2. Как связаны объем, давление и число молекул различных газов в состоянии теплового равновесия?<br> |
| | | | |
| - | | + | <br> ''Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский, Физика 10 класс'' |
| - | ''Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский, Физика 10 класс'' | + | |
| | | | |
| | <br> | | <br> |
Версия 10:53, 21 августа 2010
Гипермаркет знаний>>Физика и астрономия>>Физика 10 класс>>Физика: Определение температуры
При тепловом равновесии средняя кинетическая энергия поступательного движения молекул всех газов одинакова. В этом вы скоро убедитесь.
Средняя кинетическая энергия молекул газа при тепловом равновесии. Возьмем сосуд, разделенный пополам перегородкой, проводящей тепло. В одну половину сосуда поместим кислород, а в другую - водород, имеющие разную температуру. Спустя некоторое время газы будут иметь одинаковую температуру, не зависящую от рода газа, т. е. будут находиться в состоянии теплового равновесия. Для определения температуры выясним, какая физическая величина в молекулярно-кинетической теории обладает таким же свойством.
Из курса физики 7 класса известно, что, чем быстрее движутся молекулы, тем выше температура тела. При нагревании газа в замкнутом сосуде давление газа возрастает. Согласно же основному уравнению молекулярно-кинетической теории (8.15) давление газа p прямо пропорционально средней кинетической энергии поступательного движения молекул: 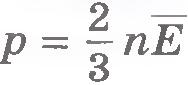 . При тепловом равновесии, если давление газа данной массы и его объем фиксированы, средняя кинетическая энергия молекул газа должна иметь строго определенное значение, как и температура. . При тепловом равновесии, если давление газа данной массы и его объем фиксированы, средняя кинетическая энергия молекул газа должна иметь строго определенное значение, как и температура.
Можно предположить, что при тепловом равновесии именно средние кинетические энергии молекул всех газов одинаковы. Конечно, это пока только предположение. Его нужно экспериментально проверить. Практически такую проверку произвести непосредственно невозможно, так как измерить среднюю кинетическую энергию молекул очень трудно. Но с помощью основного уравнения молекулярно-кинетической теории ее можно выразить через макроскопические параметры.
Так как концентрация молекул газа 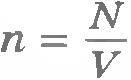 , то из уравнения (8.15) получаем , то из уравнения (8.15) получаем 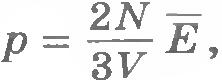 , или , или
Давление p и объем V измеряются непосредственно. Число молекул N можно определить, зная массу газа m, постоянную Авогадро NA и молярную массу M. Согласно формуле (8.8)
Если кинетическая энергия 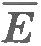 действительно одинакова для всех газов в состоянии теплового равновесия, то и величина p должна быть тоже одинаковой для всех газов. Только опыт может подтвердить или опровергнуть данное предположение. действительно одинакова для всех газов в состоянии теплового равновесия, то и величина p должна быть тоже одинаковой для всех газов. Только опыт может подтвердить или опровергнуть данное предположение.
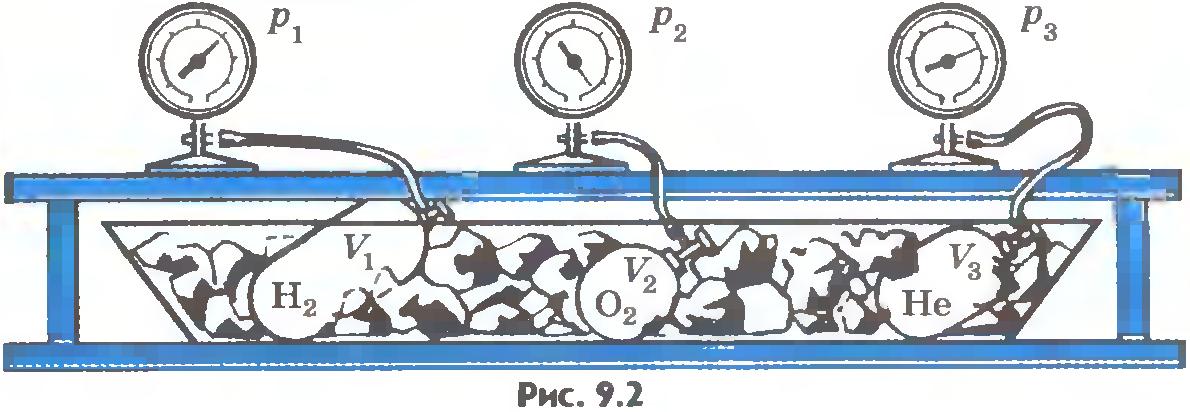
Газы в состоянии теплового равновесия. Опыт можно осуществить так. Возьмем несколько сосудов, заполненных различными газами, например водородом, гелием и кислородом. Сосуды имеют определенные объемы и снабжены манометрами. Это позволяет измерить давление в каждом сосуде. Массы газов известны, тем самым известно число молекул в каждом сосуде.
Приведем газы в состояние теплового равновесия. Для этого поместим их в тающий лед и подождем, пока не установится тепловое равновесие и давление газов перестанет меняться (рис.9.2). После этого можно утверждать, что все газы имеют одинаковую температуру 0°С. Давления газов p, их объемы V и число молекул N различны. Найдем отношение 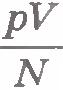 для водорода. Если, к примеру, водород, количество вещества которого равно 1 моль, занимает объем VH2=0,1 м3, то при температуре 0°С давление оказывается равным pH2=2,265•104 Па. Отсюда для водорода. Если, к примеру, водород, количество вещества которого равно 1 моль, занимает объем VH2=0,1 м3, то при температуре 0°С давление оказывается равным pH2=2,265•104 Па. Отсюда
Такое же значение отношения произведения давления газа на его объем к числу молекул получается и для всех других газов при температуре тающего льда. Обозначим это отношение через  . Тогда . Тогда
Таким образом, наше предположение оказалось верным.
Правда, соотношение (9.3) не является абсолютно точным. При давлениях в сотни атмосфер, когда газы становятся весьма плотными, отношение 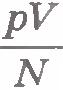 перестает быть строго определенным, не зависящим от занимаемых газами объемов. Оно выполняется для газов, когда их можно считать идеальными. перестает быть строго определенным, не зависящим от занимаемых газами объемов. Оно выполняется для газов, когда их можно считать идеальными.
Если же сосуды с газами поместить в кипящую воду при нормальном атмосферном давлении, то упомянутое отношение по-прежнему будет одним и тем же для всех газов, но больше, чем предыдущее. Как показывает опыт,
Определение температуры. Можно, следовательно, утверждать, что величина  растет с повышением температуры. Более того, растет с повышением температуры. Более того,  ни от чего, кроме температуры, не зависит. Ведь для идеальных газов ни от чего, кроме температуры, не зависит. Ведь для идеальных газов  не зависит ни от рода газа, ни от его объема или давления, а также от числа частиц в сосуде и формы самого сосуда. Этот опытный факт позволяет рассматривать величину не зависит ни от рода газа, ни от его объема или давления, а также от числа частиц в сосуде и формы самого сосуда. Этот опытный факт позволяет рассматривать величину  как естественную меру температуры, определяемую через другие макроскопические параметры газа. В принципе можно было бы считать температурой и саму величину как естественную меру температуры, определяемую через другие макроскопические параметры газа. В принципе можно было бы считать температурой и саму величину  и измерять температуру в энергетических единицах - джоулях. Однако, во-первых, это неудобно для практического использования (температуре 100°С соответствовала бы очень малая величина - порядка 10-21 Дж), а во-вторых, и это главное, уже давно принято выражать температуру в градусах. и измерять температуру в энергетических единицах - джоулях. Однако, во-первых, это неудобно для практического использования (температуре 100°С соответствовала бы очень малая величина - порядка 10-21 Дж), а во-вторых, и это главное, уже давно принято выражать температуру в градусах.
Мы нашли способ получать значения температуры, не зависящие от свойств газов, которые при этом используются. Пока что температуру мы выразили в энергетических единицах.
???
1. На каком основании можно предполагать существование связи между температурой и кинетической энергией молекул?
2. Как связаны объем, давление и число молекул различных газов в состоянии теплового равновесия?
Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский, Физика 10 класс
Материалы по физике, задание и ответы по классам, планы конспектов уроков по физике для 10 класса
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|