|
|
|
| Строка 3: |
Строка 3: |
| | ---- | | ---- |
| | | | |
| - | <u>'''<metakeywords>Геометрия, Планиметрия, 7 класс, Отрезок</metakeywords>Отрезок'''</u> | + | <u>'''<metakeywords>Геометрия, Планиметрия, 7 класс, Отрезок</metakeywords>Отрезок'''</u> |
| | | | |
| - | Отрезком называется часть прямой, которая содержит две разные точки A и B этой прямой (концы отрезка) и все точки прямой, которые лежат между ними (внутренние точки отрезка).<br> | + | Отрезком называется часть прямой, которая содержит две разные точки A и B этой прямой (концы отрезка) и все точки прямой, которые лежат между ними (внутренние точки отрезка).<br> |
| | | | |
| - | '''Отрезок прямой''' — это множество (часть прямой), состоящее из двух различных точек и всех точек, лежащих между ними. Отрезок прямой, соединяющий две точки A и B (которые называются концами отрезка), обозначается следующим образом — [A;B]. Если в обозначении отрезка опускаются квадратные скобки, то пишут «отрезок AB». Любая точка, лежащая между концами отрезка, называется его внутренней точкой. Расстояние между концами отрезка называют его длиной и обозначают как |AB|. | + | '''Отрезок прямой''' — это множество (часть прямой), состоящее из двух различных точек и всех точек, лежащих между ними. Отрезок прямой, соединяющий две точки A и B (которые называются концами отрезка), обозначается следующим образом — [A;B]. Если в обозначении отрезка опускаются квадратные скобки, то пишут «отрезок AB». Любая точка, лежащая между концами отрезка, называется его внутренней точкой. Расстояние между концами отрезка называют его длиной и обозначают как |AB|. |
| | | | |
| - | <br>Для обозначения отрезка с концами в точках A и B будем использовать символ [AB].<br><br>О точке C, принадлежащей отрезку AB, говорят также, что точка C лежит между точками A и B (если C – внутренняя точка отрезка), а также, что отрезок AB содержит точку C.<br> | + | <br>Для обозначения отрезка с концами в точках A и B будем использовать символ [AB].<br><br>О точке C, принадлежащей отрезку AB, говорят также, что точка C лежит между точками A и B (если C – внутренняя точка отрезка), а также, что отрезок AB содержит точку C.<br> |
| | | | |
| - | ''Свойство отрезка задается аксиомой:''<br>'' | + | ''Свойство отрезка задается аксиомой:''<br> |
| | | | |
| - | '''''Аксиома:'''''<br>Каждый отрезок имеет определенную длину, большую нуля. Длина отрезка равняется сумме длин частей, на которые он разбивается любой своей внутренней точкой. AB = AC + CB.<br> | + | '''''Аксиома:'''''<br>Каждый отрезок имеет определенную длину, большую нуля. Длина отрезка равняется сумме длин частей, на которые он разбивается любой своей внутренней точкой. AB = AC + CB.<br> |
| | | | |
| - | [[Image:221102010_3.jpg]] | + | [[Image:221102010 3.jpg]] |
| | | | |
| - | <br>Расстоянием между двумя точками A и B называется '''длина отрезка''' AB.<br>При этом, если точки A и B совпадают, будем считать, что расстояние между ними равно нулю.<br>Два отрезка называются равными, если равны их длины.<br><br>[[Image:221102010_4.jpg]]<br> | + | <br>Расстоянием между двумя точками A и B называется '''длина отрезка''' AB.<br>При этом, если точки A и B совпадают, будем считать, что расстояние между ними равно нулю.<br>Два отрезка называются равными, если равны их длины.<br><br>[[Image:221102010 4.jpg]]<br> |
| | | | |
| - | Отрезок '''АС=DE, CB=EF '''и'''АВ=DF''' | + | Отрезок '''АС=DE, CB=EF '''и'''АВ=DF''' |
| | | | |
| - | <br>На ''рисунке 1'' изображена прямая a и 3 точки на этой прямой: A, B, C. Точка B лежит между точками A и C, можно сказать, она разделяет точки A и C. Точки A и C лежат по разные стороны от точки B. Точки B и C расположены по одну сторону от точки A, точки A и B лежат по одну сторону от точки C. | + | <br>На ''рисунке 1'' изображена прямая a и 3 точки на этой прямой: A, B, C. Точка B лежит между точками A и C, можно сказать, она разделяет точки A и C. Точки A и C лежат по разные стороны от точки B. Точки B и C расположены по одну сторону от точки A, точки A и B лежат по одну сторону от точки C. |
| | | | |
| | + | <br> |
| | | | |
| | + | [[Image:221102010 0.jpg]]''рисунок 1''<br><br>'''Отрезок '''– часть прямой, который состоит из всех точек этой прямой, лежащих между данными точками, которые называются концами отрезка. Отрезок обозначается указанием его конечных точек. Когда говорят отрезок AB, т подразумевают отрезок с концами в точках A и B. |
| | | | |
| - | [[Image:221102010_0.jpg]]''рисунок 1''<br><br>'''Отрезок '''– часть прямой, который состоит из всех точек этой прямой, лежащих между данными точками, которые называются концами отрезка. Отрезок обозначается указанием его конечных точек. Когда говорят отрезок AB, т подразумевают отрезок с концами в точках A и B.<br><br>На данном ''рисунке 2'' мы видим отрезок AB, он является частью прямой. Точка X лежит между точками A и B, поэтому она принадлежит отрезку AB, точка Y не лежит между точками A и B, поэтому она не принадлежит отрезку AB.<br>
| + | <br>На данном ''рисунке 2'' мы видим отрезок AB, он является частью прямой. Точка X лежит между точками A и B, поэтому она принадлежит отрезку AB, точка Y не лежит между точками A и B, поэтому она не принадлежит отрезку AB.<br> |
| | | | |
| | + | <br> |
| | | | |
| - | | + | [[Image:221102010 1.jpg]]''рисунок 2'' |
| - | [[Image:221102010_1.jpg]]''рисунок 2'' | + | |
| | | | |
| | <br>''Основное свойство расположения точек на прямой – из трех точек на прямой только одна лежит между двумя точками.''<br> | | <br>''Основное свойство расположения точек на прямой – из трех точек на прямой только одна лежит между двумя точками.''<br> |
| | | | |
| - | Точка А лежит между X и Y. | + | Точка А лежит между X и Y. |
| - | | + | |
| - | Точка X [[Image:]][[Image:]]разделяет отрезок AB.
| + | |
| - | | + | |
| - | | + | |
| | | | |
| - | Обычно у отрезка прямой неважно, в каком порядке рассматриваются его концы: то есть отрезки AB и BA представляют собой один и тот же отрезок. Если у отрезка определить '''направление''', то есть порядок перечисления его концов, то такой отрезок называется направленным. Например, выше указанные направленные отрезки не совпадают. Особого обозначения у направленных отрезков нет — то, что у отрезка важно его направление обычно указывается особо.
| + | Точка X разделяет отрезок AB. |
| | | | |
| - | [[Image:221102010_5.png]]
| + | <br> |
| | | | |
| | + | Обычно у отрезка прямой неважно, в каком порядке рассматриваются его концы: то есть отрезки AB и BA представляют собой один и тот же отрезок. Если у отрезка определить '''направление''', то есть порядок перечисления его концов, то такой отрезок называется направленным. Например, выше указанные направленные отрезки не совпадают. Особого обозначения у направленных отрезков нет — то, что у отрезка важно его направление обычно указывается особо. |
| | | | |
| | + | [[Image:221102010 5.png]] |
| | | | |
| - | Дальнейшее обобщение приводит к понятию '''вектора '''— класса всех равных по длине и сонаправленных направленных отрезков.
| + | <br> |
| | | | |
| - | [[Image:221102010_6.jpg]]
| + | Дальнейшее обобщение приводит к понятию '''вектора '''— класса всех равных по длине и сонаправленных направленных отрезков. |
| | | | |
| - | <u>'''Вопросы:'''</u>
| + | [[Image:221102010 6.jpg]] |
| | | | |
| - | 1) Что такое отрезок?
| + | <u>'''Вопросы:'''</u> |
| | | | |
| - | 2) Чему равняется длина отрезка?
| + | 1) Что такое отрезок? |
| | | | |
| - | 3) Разница между отрезком и вектором?
| + | 2) Чему равняется длина отрезка? |
| | | | |
| | + | 3) Разница между отрезком и вектором? |
| | | | |
| | + | <br> |
| | | | |
| - | <u>'''Список использованных источников:'''</u> | + | <u>'''Список использованных источников:'''</u> |
| | | | |
| - | <u</u>1) http://ru.wikipedia.org
| + | 1) http://ru.wikipedia.org |
| | | | |
| - | 2) Киселев А.П. "Геометрия" (планиметрия, стереометрия) | + | 2) Киселев А.П. "Геометрия" (планиметрия, стереометрия) |
| | | | |
| - | 3) Погорелов А.В. «Геометрия. 7-9 класс» | + | 3) Погорелов А.В. «Геометрия. 7-9 класс» |
| | | | |
| | ---- | | ---- |
| Строка 75: |
Строка 77: |
| | Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - [http://xvatit.com/forum/ Образовательный форум]. | | Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - [http://xvatit.com/forum/ Образовательный форум]. |
| | | | |
| - | [[категория: Математика 7 класс]] | + | [[Category:Математика_7_класс]] |
Версия 18:11, 21 октября 2010
Гипермаркет знаний>>Математика>>Математика 7 класс. Полные уроки>>Геометрия: Отрезок. Полные уроки
Отрезок
Отрезком называется часть прямой, которая содержит две разные точки A и B этой прямой (концы отрезка) и все точки прямой, которые лежат между ними (внутренние точки отрезка).
Отрезок прямой — это множество (часть прямой), состоящее из двух различных точек и всех точек, лежащих между ними. Отрезок прямой, соединяющий две точки A и B (которые называются концами отрезка), обозначается следующим образом — [A;B]. Если в обозначении отрезка опускаются квадратные скобки, то пишут «отрезок AB». Любая точка, лежащая между концами отрезка, называется его внутренней точкой. Расстояние между концами отрезка называют его длиной и обозначают как |AB|.
Для обозначения отрезка с концами в точках A и B будем использовать символ [AB].
О точке C, принадлежащей отрезку AB, говорят также, что точка C лежит между точками A и B (если C – внутренняя точка отрезка), а также, что отрезок AB содержит точку C.
Свойство отрезка задается аксиомой:
Аксиома:
Каждый отрезок имеет определенную длину, большую нуля. Длина отрезка равняется сумме длин частей, на которые он разбивается любой своей внутренней точкой. AB = AC + CB.
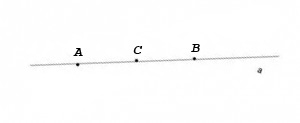
Расстоянием между двумя точками A и B называется длина отрезка AB.
При этом, если точки A и B совпадают, будем считать, что расстояние между ними равно нулю.
Два отрезка называются равными, если равны их длины.
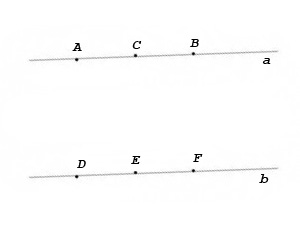
Отрезок АС=DE, CB=EF иАВ=DF
На рисунке 1 изображена прямая a и 3 точки на этой прямой: A, B, C. Точка B лежит между точками A и C, можно сказать, она разделяет точки A и C. Точки A и C лежат по разные стороны от точки B. Точки B и C расположены по одну сторону от точки A, точки A и B лежат по одну сторону от точки C.
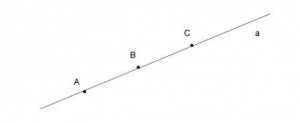 рисунок 1 рисунок 1
Отрезок – часть прямой, который состоит из всех точек этой прямой, лежащих между данными точками, которые называются концами отрезка. Отрезок обозначается указанием его конечных точек. Когда говорят отрезок AB, т подразумевают отрезок с концами в точках A и B.
На данном рисунке 2 мы видим отрезок AB, он является частью прямой. Точка X лежит между точками A и B, поэтому она принадлежит отрезку AB, точка Y не лежит между точками A и B, поэтому она не принадлежит отрезку AB.
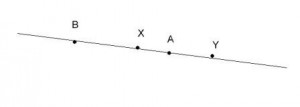 рисунок 2 рисунок 2
Основное свойство расположения точек на прямой – из трех точек на прямой только одна лежит между двумя точками.
Точка А лежит между X и Y.
Точка X разделяет отрезок AB.
Обычно у отрезка прямой неважно, в каком порядке рассматриваются его концы: то есть отрезки AB и BA представляют собой один и тот же отрезок. Если у отрезка определить направление, то есть порядок перечисления его концов, то такой отрезок называется направленным. Например, выше указанные направленные отрезки не совпадают. Особого обозначения у направленных отрезков нет — то, что у отрезка важно его направление обычно указывается особо.

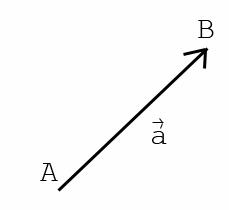
Дальнейшее обобщение приводит к понятию вектора — класса всех равных по длине и сонаправленных направленных отрезков.
Вопросы:
1) Что такое отрезок?
2) Чему равняется длина отрезка?
3) Разница между отрезком и вектором?
Список использованных источников:
1) http://ru.wikipedia.org
2) Киселев А.П. "Геометрия" (планиметрия, стереометрия)
3) Погорелов А.В. «Геометрия. 7-9 класс»
Отредактировано и выслано Потурнаком С .А.
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
Предмети > Математика > Математика 7 класс
|
















