|
|
|
| Строка 17: |
Строка 17: |
| | Повернем плоскость Н вокруг оси ОХ на 90° вниз, до совмещения с плоскостью V, как показано на рис. 105. Получим ортогональные проекции точки. Обратите внимание на то, что проекции а и а' расположились на одной прямой а'а (рис. 105). Линия аа' называется линией проекционной связи.<br> | | Повернем плоскость Н вокруг оси ОХ на 90° вниз, до совмещения с плоскостью V, как показано на рис. 105. Получим ортогональные проекции точки. Обратите внимание на то, что проекции а и а' расположились на одной прямой а'а (рис. 105). Линия аа' называется линией проекционной связи.<br> |
| | | | |
| - | [[Image:Чер85.jpg|181x306px]] | + | [[Image:Чер85.jpg|181x306px|Чер85.jpg]] |
| | | | |
| | '''Выводы:'''<br> <br>1. Фронтальная и горизонтальная проекции точки всегда находятся на перпендикуляре к оси проекций ох, называемом линией проекционной связи.<br>2. Отрезок аа<sub>x</sub> — есть расстояние точки А до плоскости V.<br>3. Отрезок а'а<sub>x</sub> — расстояние точки А до плоскости Н.<br>4. Положение точки в пространстве определяют две ее проекции.<br> Прямоугольное (ортогональное) проецирование точки на три плоскости проекций.<br>Рассмотрим проецирование точки А на три взаимно перпендикулярные плоскости. К фронтальной и горизонтальной плоскостям проекций добавим третью — профильную плоскость проекций (W — «дубль вэ»), которую расположим перпендикулярно к плоскостям V и Н. Используя метод ортогонального проецирования, отобразим точку на трех плоскостях проекций. На профильной плоскости проекций получим изображение, которое будем называть профильной проекцией точки. Профильная проекция обозначается а", а читается как «а два штриха» (рис. 106).<br> Плоскости проекций Н и W разворачивают до совмещения с плоскостью V, как показано на рис. 106, 107.<br> Линии пересечения плоскостей являются осями проекций ох, оу, ох (рис. 106). Обратим внимание на то, что проекции а' и а, а' и а", а и а" лежат на прямых, называемых линиями проекционной связи (рис. 107). Такая зависимость в расположении проекций точки называется проекционной связью и при выполнении чертежей должна обязательно соблюдаться. Чертеж, состоящий из нескольких прямоугольных проекций, называется чертежом в системе прямоугольных проекций, или ортогональным чертежом. | | '''Выводы:'''<br> <br>1. Фронтальная и горизонтальная проекции точки всегда находятся на перпендикуляре к оси проекций ох, называемом линией проекционной связи.<br>2. Отрезок аа<sub>x</sub> — есть расстояние точки А до плоскости V.<br>3. Отрезок а'а<sub>x</sub> — расстояние точки А до плоскости Н.<br>4. Положение точки в пространстве определяют две ее проекции.<br> Прямоугольное (ортогональное) проецирование точки на три плоскости проекций.<br>Рассмотрим проецирование точки А на три взаимно перпендикулярные плоскости. К фронтальной и горизонтальной плоскостям проекций добавим третью — профильную плоскость проекций (W — «дубль вэ»), которую расположим перпендикулярно к плоскостям V и Н. Используя метод ортогонального проецирования, отобразим точку на трех плоскостях проекций. На профильной плоскости проекций получим изображение, которое будем называть профильной проекцией точки. Профильная проекция обозначается а", а читается как «а два штриха» (рис. 106).<br> Плоскости проекций Н и W разворачивают до совмещения с плоскостью V, как показано на рис. 106, 107.<br> Линии пересечения плоскостей являются осями проекций ох, оу, ох (рис. 106). Обратим внимание на то, что проекции а' и а, а' и а", а и а" лежат на прямых, называемых линиями проекционной связи (рис. 107). Такая зависимость в расположении проекций точки называется проекционной связью и при выполнении чертежей должна обязательно соблюдаться. Чертеж, состоящий из нескольких прямоугольных проекций, называется чертежом в системе прямоугольных проекций, или ортогональным чертежом. |
| | | | |
| - | [[Image:Чер86.jpg|256x292px]][[Image:Чер87.jpg|455x294px]] | + | [[Image:Чер86.jpg|256x292px|Чер86.jpg]][[Image:Чер87.jpg|455x294px|Чер87.jpg]] |
| | | | |
| - | Чертеж точки в системе прямоугольных проекций представлен на рис. 107, б.Построение третьей проекции точки по двум заданным.<br>Если известны любые две проекции точки (например, а и а'), то можно найти третью проекцию (в нашем примере а"). Для этого можно использовать постоянную прямую чертежа, которая проводится под углом 45° (рис. 108). Через заданные проекции а и а' точки А проводим линии связи перпендикулярно к осям oz и оу. Точки пересечения линий связи дают искомую проекцию а". Перенос линии проекционной связи с оси оун на ось oyw осуществляется с помощью постоянной прямой I (рис. 108). Так с помощью вспомогательной прямой находится третья проекция а" точки А по двум заданным.<br> Профильную проекцию а" точки А можно найти способом координирования, показанным на рис. 109. Из точки а' проведем линию проекционной связи к оси z, на ней отложим отрезок aza" = аха. Обратите внимание на то, что расстояние от оси z до профильной проекции точки равно расстоянию от оси х до ее горизонтальной проекции.<br>[[Image:чер88.jpg]]<br> | + | Чертеж точки в системе прямоугольных проекций представлен на рис. 107, б.Построение третьей проекции точки по двум заданным.<br>Если известны любые две проекции точки (например, а и а'), то можно найти третью проекцию (в нашем примере а"). Для этого можно использовать постоянную прямую чертежа, которая проводится под углом 45° (рис. 108). Через заданные проекции а и а' точки А проводим линии связи перпендикулярно к осям oz и оу. Точки пересечения линий связи дают искомую проекцию а". Перенос линии проекционной связи с оси оун на ось oyw осуществляется с помощью постоянной прямой I (рис. 108). Так с помощью вспомогательной прямой находится третья проекция а" точки А по двум заданным. |
| | | | |
| | + | [[Image:Чер88.jpg|252x273px]]<br> Профильную проекцию а" точки А можно найти способом координирования, показанным на рис. 109. Из точки а' проведем линию проекционной связи к оси z, на ней отложим отрезок aza" = аха. Обратите внимание на то, что расстояние от оси z до профильной проекции точки равно расстоянию от оси х до ее горизонтальной проекции.<br>[[Image:чер89.jpg]]<br> |
| | | | |
| | + | |
| | + | |
| | + | <br> |
| | | | |
| | <br> | | <br> |
Версия 20:48, 27 декабря 2010
Гипермаркет знаний>>Черчение 9 класс>>Черчение: Чертежи в системе прямоугольных проекций
Вы научились строить аксонометрические изображения, в основу которых положено параллельное проецирование. С помощью параллельного проецирования можно построить и другие изображения.
Наиболее широко применяемыми в технике являются изображения, которые получены при прямоугольном проецировании на одну, две и три взаимно перпендикулярные плоскости проекций.
Прямоугольное (ортогональное) проецирование точки на одну плоскость проекций.Рассмотрим самый простой случай — ортогональное проецирование точки (рис. 102).
Перед плоскостью проекций поместим точку А и через нее проведем проецирующий луч ва под пря¬мым углом к плоскости проекций до пересечения с ней. Получим точку а — проекцию точки А.

Вывод:
1.Проекция точки на данную плоскость проекций есть точка.
2.Любая проецируемая точка имеет одну проекцию на выбранной плоскости проекций.
3.Проекция точки, лежащей на плоскости проекций, совпадает с самой точкой.
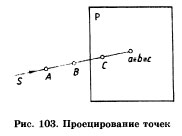
Рассмотрим другой пример. На проецирующем луче разместим три точки: А, В, С (рис. 103). Их проекцией на плоскости Р является точка а, следовательно, а=Ь=c. По одной проекции нельзя определить, сколько объектов (точек) было на нее спроецировано.
Вывод:
1. Любое количество точек, находящихся на одном проецирующем луче, проецируется в одну точку.
2. Для определения положения точки в пространстве одной ее проекции недостаточно.
Прямоугольное (ортогональное) проецирование точки на две плоскости проекций.
Метод выполнения прямоугольных изображений на две взаимно перпендикулярные плоскости проекций впервые был разработан в 1799 году французским инженером и ученым Гаспаром Монжем, который считается основоположником начертательной геометрии — науки об изображении предметов и графических способах решения задач.
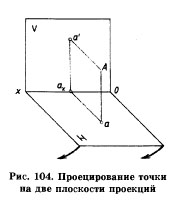
Для того чтобы получить две проекции точки, определяющих положение ее в пространстве, возьмем две взаимно перпендикулярные плоскости: V — фронтальную и Н — горизонтальную. Они будут пересекаться по прямой ох, которую называют осью проекций (рис. 104).
Расположим точку А в двугранном углу. Используя метод прямоугольного проецирования, спроецируем ее на плоскости проекций, получим фронтальную (а') и горизонтальную (а) проекции точки А. Запись а' читается как «а штрих».
Мы рассмотрели метод получения изображений точки А в системе двух плоскостей проекций. Чтобы решить обратную задачу: по изображениям точки найти ее положение в пространстве, необходимо от проекций а и а' провести проецирующие лучи перпендикулярно плоскостям проекций. Их пересечение определит положение точки А в пространстве.
Повернем плоскость Н вокруг оси ОХ на 90° вниз, до совмещения с плоскостью V, как показано на рис. 105. Получим ортогональные проекции точки. Обратите внимание на то, что проекции а и а' расположились на одной прямой а'а (рис. 105). Линия аа' называется линией проекционной связи.
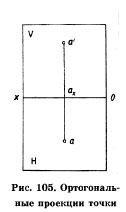
Выводы:
1. Фронтальная и горизонтальная проекции точки всегда находятся на перпендикуляре к оси проекций ох, называемом линией проекционной связи.
2. Отрезок ааx — есть расстояние точки А до плоскости V.
3. Отрезок а'аx — расстояние точки А до плоскости Н.
4. Положение точки в пространстве определяют две ее проекции.
Прямоугольное (ортогональное) проецирование точки на три плоскости проекций.
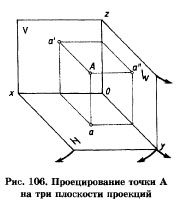
Рассмотрим проецирование точки А на три взаимно перпендикулярные плоскости. К фронтальной и горизонтальной плоскостям проекций добавим третью — профильную плоскость проекций (W — «дубль вэ»), которую расположим перпендикулярно к плоскостям V и Н. Используя метод ортогонального проецирования, отобразим точку на трех плоскостях проекций. На профильной плоскости проекций получим изображение, которое будем называть профильной проекцией точки. Профильная проекция обозначается а", а читается как «а два штриха» (рис. 106).
Плоскости проекций Н и W разворачивают до совмещения с плоскостью V, как показано на рис. 106, 107.
Линии пересечения плоскостей являются осями проекций ох, оу, ох (рис. 106). Обратим внимание на то, что проекции а' и а, а' и а", а и а" лежат на прямых, называемых линиями проекционной связи (рис. 107). Такая зависимость в расположении проекций точки называется проекционной связью и при выполнении чертежей должна обязательно соблюдаться. Чертеж, состоящий из нескольких прямоугольных проекций, называется чертежом в системе прямоугольных проекций, или ортогональным чертежом.
 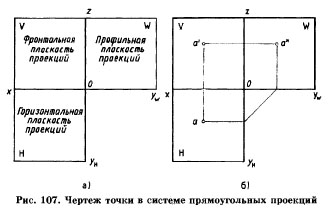
Чертеж точки в системе прямоугольных проекций представлен на рис. 107, б.Построение третьей проекции точки по двум заданным.
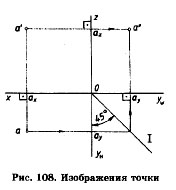
Если известны любые две проекции точки (например, а и а'), то можно найти третью проекцию (в нашем примере а"). Для этого можно использовать постоянную прямую чертежа, которая проводится под углом 45° (рис. 108). Через заданные проекции а и а' точки А проводим линии связи перпендикулярно к осям oz и оу. Точки пересечения линий связи дают искомую проекцию а". Перенос линии проекционной связи с оси оун на ось oyw осуществляется с помощью постоянной прямой I (рис. 108). Так с помощью вспомогательной прямой находится третья проекция а" точки А по двум заданным.
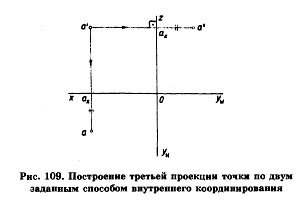
Профильную проекцию а" точки А можно найти способом координирования, показанным на рис. 109. Из точки а' проведем линию проекционной связи к оси z, на ней отложим отрезок aza" = аха. Обратите внимание на то, что расстояние от оси z до профильной проекции точки равно расстоянию от оси х до ее горизонтальной проекции.
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|


















