Построение и деление углов — Гипермаркет знаний

KNOWLEDGE HYPERMARKET

Построение и деление углов

 		Версия 13:36, 11 января 2011 (просмотреть исходный код)
User12  (Обсуждение | вклад)
← Предыдущая правка
		Текущая версия на 13:09, 27 августа 2012 (просмотреть исходный код)
ВикторияМора  (Обсуждение | вклад) 
 
		
Строка 1:
Строка 1:
- '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]&gt;&gt;[[Черчение 9 класс|Черчение 9 класс]]&gt;&gt;Черчение: Построение и деление углов '''   + '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]&gt;&gt;[[Черчение|Черчение]]&gt;&gt;[[Черчение 9 класс|Черчение 9 класс]]&gt;&gt;Черчение: Построение и деление углов '''  
  
 <metakeywords>Построение и деление углов</metakeywords><br>    <metakeywords>Построение и деление углов</metakeywords><br>  
Строка 5:
Строка 5:
 <br>    <br>  
  
- &nbsp;&nbsp;&nbsp;&nbsp;&nbsp; Построение углов при помощи угольников. При помощи линейки и угольников с углами 30°, 60°, 90° и 45°, 45°, 90° можно построить любой угол, кратный 15°, в зависимости от того, в какой комбинации будем сочетать их углы. Внимательно рассмотрите положение угольников при построении различных углов (рис. 62) и используйте эти знания при выполнении чертежей.<br>&nbsp;&nbsp;&nbsp;&nbsp; Деление углов на равные части. Чтобы разделить прямой угол (например угол ABC) на три равные части, из вершины угла (точки В) проводим дугу произвольного радиуса R до пересечения со сторонами угла в точках D и Е. Из точек D и Е, как из центров, радиусом R = ВЕ или BD, проводим дуги,пересекающие дугу БЕ в точках Р и Н, получим углы АВР = РВН = НВЕ = 30° (рис. 63).<br>&nbsp;&nbsp;&nbsp; Деление угла на две равные части и построение угла, равного данному, вы изучали на уроках геометрии. Вспомните этот материал самостоятельно, вам он понадобится на уроках черчения.<br>&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; [[Image:Чер52.jpg|275x340px|Чер52.jpg]]<br>&nbsp;&nbsp;&nbsp;&nbsp; С помощью транспортира можно построить любой угол и разделить его на равные части. + '''Построение '''[[Откладывание_отрезков_и_углов._Полные_уроки|'''углов''']]'''при помощи угольников'''. При помощи линейки и угольников с углами 30°, 60°, 90° и 45°, 45°, 90° можно построить любой угол, кратный 15°, в зависимости от того, в какой комбинации будем сочетать их углы. Внимательно рассмотрите положение угольников при построении различных углов (рис. 62) и используйте эти знания при выполнении чертежей.<br>  
  
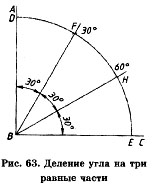
  + '''Деление углов на равные части'''. Чтобы разделить прямой угол (например угол ABC) на три равные части, из вершины угла (точки В) проводим дугу произвольного радиуса R до пересечения со сторонами угла в точках D и Е. Из точек D и Е, как из центров, радиусом R = ВЕ или BD, проводим дуги, пересекающие дугу БЕ в точках Р и Н, получим углы АВР = РВН = НВЕ = 30° (рис. 63).<br> 
  + 
  + Деление угла на две равные части и построение угла, равного данному, вы изучали на уроках [[Алгебра_и_геометрия|геометрии]]. Вспомните этот материал самостоятельно, вам он понадобится на уроках [[Черчение|черчения]]. 
  + 
  + <br>&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; [[Image:Чер52.jpg|200px|деление угла]]<br>
  + 
  + С помощью транспортира можно построить любой угол и разделить его на равные части. 
  + 
  + <br> 
  + 
  + ''Н.А.Гордеенко, В.В.Степакова - Черчение.,[[9_класс_уроки|9 класс]]<br>Отослано читателями из интернет-сайтов''
  
  
- Н.А.Гордеенко, В.В.Степакова - Черчение.,9 класс<br>Отослано читателями из интернет-сайтов  
  
   '''<u>Содержание урока</u>'''    '''<u>Содержание урока</u>'''
Строка 25:
Строка 35:
   [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы    [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы
   [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников    [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников
-   +  
   '''<u>Иллюстрации</u>'''    '''<u>Иллюстрации</u>'''
   '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа '''    '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа '''
Строка 47:
Строка 57:
   [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке      [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке  
   [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми      [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми  
-   +  
   '''<u>Только для учителей</u>'''    '''<u>Только для учителей</u>'''
   '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки '''    '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки '''
Строка 56:
Строка 66:
         
         
-   '''<u>Интегрированные уроки</u>'''<u> +  '''<u>Интегрированные уроки</u>'''<u>
   </u>    </u>
  

Текущая версия на 13:09, 27 августа 2012
Гипермаркет знаний>>Черчение>>Черчение 9 класс>>Черчение: Построение и деление углов  

 

 
Построение угловпри помощи угольников. При помощи линейки и угольников с углами 30°, 60°, 90° и 45°, 45°, 90° можно построить любой угол, кратный 15°, в зависимости от того, в какой комбинации будем сочетать их углы. Внимательно рассмотрите положение угольников при построении различных углов (рис. 62) и используйте эти знания при выполнении чертежей.
 
Деление углов на равные части. Чтобы разделить прямой угол (например угол ABC) на три равные части, из вершины угла (точки В) проводим дугу произвольного радиуса R до пересечения со сторонами угла в точках D и Е. Из точек D и Е, как из центров, радиусом R = ВЕ или BD, проводим дуги, пересекающие дугу БЕ в точках Р и Н, получим углы АВР = РВН = НВЕ = 30° (рис. 63).
 
Деление угла на две равные части и построение угла, равного данному, вы изучали на уроках геометрии. Вспомните этот материал самостоятельно, вам он понадобится на уроках черчения. 

                                                                       

С помощью транспортира можно построить любой угол и разделить его на равные части. 

 
Н.А.Гордеенко, В.В.Степакова - Черчение.,9 класс
Отослано читателями из интернет-сайтов



Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников

Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 

Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки



 
Если у вас есть исправления или предложения к данному уроку, напишите нам. 
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.

Источник — «http://edufuture.biz/index.php?title=%D0%9F%D0%BE%D1%81%D1%82%D1%80%D0%BE%D0%B5%D0%BD%D0%B8%D0%B5_%D0%B8_%D0%B4%D0%B5%D0%BB%D0%B5%D0%BD%D0%B8%D0%B5_%D1%83%D0%B3%D0%BB%D0%BE%D0%B2»
@@ Строка 1: / Строка 1: @@
-'''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]&gt;&gt;[[Черчение 9 класс|Черчение 9 класс]]&gt;&gt;Черчение: Построение и деление углов '''
+'''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]&gt;&gt;[[Черчение|Черчение]]&gt;&gt;[[Черчение 9 класс|Черчение 9 класс]]&gt;&gt;Черчение: Построение и деление углов '''
 <metakeywords>Построение и деление углов</metakeywords><br>
@@ Строка 5: / Строка 5: @@
 <br>
-&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; Построение углов при помощи угольников. При помощи линейки и угольников с углами 30°, 60°, 90° и 45°, 45°, 90° можно построить любой угол, кратный 15°, в зависимости от того, в какой комбинации будем сочетать их углы. Внимательно рассмотрите положение угольников при построении различных углов (рис. 62) и используйте эти знания при выполнении чертежей.<br>&nbsp;&nbsp;&nbsp;&nbsp; Деление углов на равные части. Чтобы разделить прямой угол (например угол ABC) на три равные части, из вершины угла (точки В) проводим дугу произвольного радиуса R до пересечения со сторонами угла в точках D и Е. Из точек D и Е, как из центров, радиусом R = ВЕ или BD, проводим дуги,пересекающие дугу БЕ в точках Р и Н, получим углы АВР = РВН = НВЕ = 30° (рис. 63).<br>&nbsp;&nbsp;&nbsp; Деление угла на две равные части и построение угла, равного данному, вы изучали на уроках геометрии. Вспомните этот материал самостоятельно, вам он понадобится на уроках черчения.<br>&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; [[Image:Чер52.jpg|275x340px|Чер52.jpg]]<br>&nbsp;&nbsp;&nbsp;&nbsp; С помощью транспортира можно построить любой угол и разделить его на равные части.
+'''Построение '''[[Откладывание_отрезков_и_углов._Полные_уроки|'''углов''']]'''при помощи угольников'''. При помощи линейки и угольников с углами 30°, 60°, 90° и 45°, 45°, 90° можно построить любой угол, кратный 15°, в зависимости от того, в какой комбинации будем сочетать их углы. Внимательно рассмотрите положение угольников при построении различных углов (рис. 62) и используйте эти знания при выполнении чертежей.<br>
+'''Деление углов на равные части'''. Чтобы разделить прямой угол (например угол ABC) на три равные части, из вершины угла (точки В) проводим дугу произвольного радиуса R до пересечения со сторонами угла в точках D и Е. Из точек D и Е, как из центров, радиусом R = ВЕ или BD, проводим дуги, пересекающие дугу БЕ в точках Р и Н, получим углы АВР = РВН = НВЕ = 30° (рис. 63).<br>
+Деление угла на две равные части и построение угла, равного данному, вы изучали на уроках [[Алгебра_и_геометрия|геометрии]]. Вспомните этот материал самостоятельно, вам он понадобится на уроках [[Черчение|черчения]].
+<br>&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; [[Image:Чер52.jpg|200px|деление угла]]<br>
+С помощью транспортира можно построить любой угол и разделить его на равные части.
+<br>
+''Н.А.Гордеенко, В.В.Степакова - Черчение.,[[9_класс_уроки|9 класс]]<br>Отослано читателями из интернет-сайтов''
-Н.А.Гордеенко, В.В.Степакова - Черчение.,9 класс<br>Отослано читателями из интернет-сайтов
   '''<u>Содержание урока</u>'''
@@ Строка 25: / Строка 35: @@
   [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы
   [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников
   '''<u>Иллюстрации</u>'''
   '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа '''
@@ Строка 47: / Строка 57: @@
   [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке
   [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми
   '''<u>Только для учителей</u>'''
   '''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки '''
@@ Строка 56: / Строка 66: @@
-  '''<u>Интегрированные уроки</u>'''<u>
+ '''<u>Интегрированные уроки</u>'''<u>
   </u>

При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов - гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.

Разработка - Гипермаркет знаний 2008-

Ждем Ваши замечания и предложения на email:
По вопросам рекламы и спонсорства пишите на email: