|
|
|
| Строка 11: |
Строка 11: |
| | <br> | | <br> |
| | | | |
| - | <br> 6. Тотожні вирази. Тотожні перетворення виразів<br>Мета: зрозуміти, що таке тотожності. Дізнатися, які вирази є тотожно рівними. Згадати формули скороченого множення. Дізнатися,що таке умовні тотожності.<br><br>1. Тотожнорівні вирази. Тотожне перетворення виразу.<br>2. Умовні тотожності.<br><br>1. Тотожнорівні вирази. Тотожне перетворення виразу<br><br>Розглянемо 2 приклада: х2-2х і 4х-5. При х=2 маємо: 2*2-2*2=0 і 4*2-5=3. Числа 0 та 3 називаються відповідними значеннями виразів х2-2х і 4х-5 при х=2. Знайдемо значення цих виразів при х=1. Маємо:<br>1*1-2*1=-1 і 4*1-5=-1.<br>Відповідні значення двох виразів можуть бути однаковими,а можуть і відрізнятися. Якщо значення рівні,то вирази назіваються тотожними.<br><br>Два вирази називаються тотожно рівними, якщо при будь-яких допустимих значеннях букв відповідні значення цих виразів дорівнюють одне одному.<br><br>Рівність, яка є правильною при будь-яких значеннях букв, називається тотожністю.<br><br>Заміна виразу тотожно рівним йому виразом називається тотожним перетворенням виразу.<br><br>Приклади тотожностей:<br>1) a+b=b+a<br>2)a+0=a<br>3) 3a+5a-7=8а-5-2.<br><br>А ось 4а-3с+1=2а+5с-2 не є тотожністю,бо ,наприклад, при а=1 та с=0 вони не дорівнюють один одному.<br><br><br>Тотожне перетворення алгебраїчного виразу – заміна цього виразу іншим, тотожно рівним йому. <br>Спростити алгебраїчний вираз – означає замінити його на тотожно рівний, але найпростіший за записом. Як видно з означення, спрощення алгебраїчного виразу є тотожним перетворенням. Розглянемо приклад спрощення. <br>1. Спростити вираз (x-y)(x+2y)-x2+2y2.<br>(x-y)(x+2y)-x2+2y2=x*x+2xy-xy-2y*y-x2+2y2=xy.<br><br><br>З деякими видами тотожних перетворень ви уже знайомі: розкриття дужок і, навпаки, винесення спільного множника за дужки; множення чисельника і знаменника дробу на одне й те ж саме число, що не дорівнює 0 – все це тотожні перетворення. <br>При проведенні тотожних перетворень часто стають корисними формули скороченого множення. Основні з них: <br><br><br><br>Пишеться Читається<br> <br>квадрат суми двох виразів дорівнює квадрат першого виразу додати подвоєний добуток цих виразів додати квадрат другого виразу.<br> <br>квадрат різниці двох виразів дорівнює квадрат першого виразу відняти подвоєний добуток цих виразів додати квадрат другого виразу.<br> <br>різниця квадратів двох виразів дорівнює добутку різниці та суми цих виразів.<br> <br> <br>куб суми двох виразів дорівнює куб першого виразу додати потроєний добуток квадрату першого та другого виразу додати потроєний добуток першого та квадрату другого виразу додати куб другого виразу.<br> <br>куб різниці двох виразів = куб першого виразу відняти потроєний добуток квадрату першого та другого виразу додати потроєний добуток першого та квадрату другого виразу відняти куб другого виразу.<br> <br>сума кубів двох виразів дорівнює добутку суми цих виразів та неповному квадрату різниці цих виразів (квадрат першого виразу відняти добуток цих виразів додати квадрат другого виразу).<br> <br>різниця кубів двох виразів дорівнює добутку різниці цих виразів та неповному квадрату суми цих виразів ( квадрат першого виразу додати добуток цих виразів додати квадрат другого виразу).<br> <br> <br>в четвертому степені сума двох виразів дорівнює в четвертому степені перший вираз додати помножений на 4 добуток кубу першого та другого виразу додати помножений на 6 добуток квадрату першого та квадрату другого виразу додати помножений на 4 добуток першого та кубу другого виразу додати в четвертому степені другий вираз.<br> <br>в четвертому степені різниця двох виразів дорівнює в четвертому степені перший вираз відняти помножений на 4 добуток кубу першого та другого виразу додати помножений на 6 добуток квадрату першого та квадрату другого виразу відняти помножений на 4 добуток першого та кубу другого виразу додати в четвертому степені другий вираз.<br> <br> <br> <br>квадрат суми трьох виразів дорівнює квадрат першого виразу додати квадрат другого виразу додати квадрат третього виразу додати подвоєний добуток першого та другого виразу додати подвоєний добуток першого та третього виразу додати подвоєний добуток другого та третього виразу.<br> <br>квадрат різниці трьох виразів дорівнює квадрат першого виразу додати квадрат другого виразу додати квадрат третього виразу відняти подвоєний добуток першого та другого виразу відняти подвоєний добуток першого та третього виразу додати подвоєний добуток другого та третього виразу.<br><br><br>Відмітимо, що всі ці формули – тотожності: вони правильні для будь-яких значень.<br><br>http://www.youtube.com/watch?v=yn8SLQzYx-I<br><br><br><br> <br><br>Перевір себе!<br>1. З написаних виразів складіть формули скороченого множення:<br>Виберіть у правій колонці формулу і сформулюйте правила, що відповідають даним формулам. <br>Квадрат суми<br>Квадрат різниці <br>Різниця квадратів <br>Куб суми <br>Куб різниці <br> <br>а2 – b2<br>( а + b)2<br>( а - b)3<br>( а - b)2<br>( а + b)3<br>а2 – 2а b + b2<br>( а – b)(а + b)<br>а2 + 2а b + b2<br>( а + b)( а2 – 2а b + b2)<br>( а - b)( а2 + 2а b + b2)<br><br><br>Кубу першого виразу, плюс потроєний добуток квадрата першого виразу на другий, плюс потроєний добуток першого на квадрат другого, плюс куб другого виразу. <br>Добутку їх суми на різницю.<br>Квадрату першого члена плюс подвоєний добуток першого на другий, плюс квадрат другого члена<br>Квадрату першого члена мінус подвоєний добуток першого на другий, плюс квадрат другого члена.<br>Кубу першого виразу, мінус потроєний добуток квадрата першого виразу на другий, плюс потроєний добуток першого на квадрат другого, мінус куб другого виразу. <br><br> <br><br>Список використаної літератури:<br>1. Урок на тему «Тотожні вирази» викладача Конченко Т. М. , Гімназії міжнародних відносин, м. Київ (СЗШ №323).<br>2. Урок на тему «Перетворення тотожних виразів» викладача Конченко Т. М. , Гімназії міжнародних відносин, м. Київ (СЗШ №323).<br>3. Істер О. А. «Алгебра. 7 клас».<br>4. Мерзляк А. Г., Полонський В. Б., Рабінович Ю. М., ЯкірМ. С. Збірник задачізавдань для тематичного оцінювання з алгебри для 7 класу. – Харків, Гімназія, 2004. – 112 с.: іл.<br><br><br>
| + | <br> <u>'''Мета:'''</u> зрозуміти, що таке тотожності. Дізнатися, які вирази є тотожно рівними. Згадати формули скороченого множення. Дізнатися,що таке умовні тотожності.<br><br>1. Тотожнорівні вирази. Тотожне перетворення виразу.<br>2. Умовні тотожності.<br><br><u>'''1. Тотожнорівні вирази. Тотожне перетворення виразу'''</u><br><br>Розглянемо 2 приклада: х2-2х і 4х-5. При х=2 маємо: 2*2-2*2=0 і 4*2-5=3. Числа 0 та 3 називаються відповідними значеннями виразів х2-2х і 4х-5 при х=2. Знайдемо значення цих виразів при х=1. Маємо:<br>1*1-2*1=-1 і 4*1-5=-1.<br>Відповідні значення двох виразів можуть бути однаковими,а можуть і відрізнятися. Якщо значення рівні,то вирази назіваються тотожними.<br><br>Два вирази називаються '''тотожно рівними''', якщо при будь-яких допустимих значеннях букв відповідні значення цих виразів дорівнюють одне одному.<br><br>Рівність, яка є правильною при будь-яких значеннях букв, називається '''тотожністю'''.<br><br>Заміна виразу тотожно рівним йому виразом називається '''тотожним перетворенням виразу.'''<br><br>Приклади тотожностей: |
| | + | |
| | + | 1) a+b=b+a<br>2) a+0=a<br>3) 3a+5a-7=8а-5-2.<br><br>''А ось 4а-3с+1=2а+5с-2 не є тотожністю,бо ,наприклад, при а=1 та с=0 вони не дорівнюють один одному.'' |
| | + | |
| | + | ''Тотожне перетворення алгебраїчного виразу'' – заміна цього виразу іншим, тотожно рівним йому. <br>Спростити алгебраїчний вираз – означає замінити його на тотожно рівний, але найпростіший за записом. Як видно з означення, спрощення алгебраїчного виразу є тотожним перетворенням. Розглянемо приклад спрощення. |
| | + | |
| | + | 1. Спростити вираз (x-y)(x+2y)-x2+2y2.<br>(x-y)(x+2y)-x2+2y2=x*x+2xy-xy-2y*y-x2+2y2=xy.<br><br>З деякими видами тотожних перетворень ви уже знайомі: розкриття дужок і, навпаки, винесення спільного множника за дужки; множення чисельника і знаменника дробу на одне й те ж саме число, що не дорівнює 0 – все це тотожні перетворення. <br>При проведенні тотожних перетворень часто стають корисними формули скороченого множення. Основні з них: <br><br> |
| | + | |
| | + | {| cellspacing="1" cellpadding="1" border="1" style="width: 797px; height: 360px;" |
| | + | |- |
| | + | | '''Пишеться <br>''' |
| | + | | ''' Читається''' |
| | + | |- |
| | + | | [[Image:1801-13.jpg]] |
| | + | | квадрат суми двох виразів дорівнює квадрат першого виразу додати подвоєний добуток цих виразів додати квадрат другого виразу. |
| | + | |- |
| | + | | [[Image:1801-14.jpg]] |
| | + | | квадрат різниці двох виразів дорівнює квадрат першого виразу відняти подвоєний добуток цих виразів додати квадрат другого виразу. |
| | + | |- |
| | + | | [[Image:1801-15.jpg]] |
| | + | | різниця квадратів двох виразів дорівнює добутку різниці та суми цих виразів. |
| | + | |- |
| | + | | |
| | + | | |
| | + | |- |
| | + | | |
| | + | | |
| | + | |- |
| | + | | |
| | + | | |
| | + | |- |
| | + | | |
| | + | | |
| | + | |- |
| | + | | |
| | + | | |
| | + | |- |
| | + | | |
| | + | | |
| | + | |- |
| | + | | |
| | + | | |
| | + | |- |
| | + | | |
| | + | | |
| | + | |- |
| | + | | |
| | + | | |
| | + | |- |
| | + | | |
| | + | | |
| | + | |- |
| | + | | |
| | + | | |
| | + | |- |
| | + | | |
| | + | | |
| | + | |- |
| | + | | |
| | + | | |
| | + | |} |
| | + | |
| | + | <br><br> <br><br> <br> <br>куб суми двох виразів дорівнює куб першого виразу додати потроєний добуток квадрату першого та другого виразу додати потроєний добуток першого та квадрату другого виразу додати куб другого виразу.<br> <br>куб різниці двох виразів = куб першого виразу відняти потроєний добуток квадрату першого та другого виразу додати потроєний добуток першого та квадрату другого виразу відняти куб другого виразу.<br> <br>сума кубів двох виразів дорівнює добутку суми цих виразів та неповному квадрату різниці цих виразів (квадрат першого виразу відняти добуток цих виразів додати квадрат другого виразу).<br> <br>різниця кубів двох виразів дорівнює добутку різниці цих виразів та неповному квадрату суми цих виразів ( квадрат першого виразу додати добуток цих виразів додати квадрат другого виразу).<br> <br> <br>в четвертому степені сума двох виразів дорівнює в четвертому степені перший вираз додати помножений на 4 добуток кубу першого та другого виразу додати помножений на 6 добуток квадрату першого та квадрату другого виразу додати помножений на 4 добуток першого та кубу другого виразу додати в четвертому степені другий вираз.<br> <br>в четвертому степені різниця двох виразів дорівнює в четвертому степені перший вираз відняти помножений на 4 добуток кубу першого та другого виразу додати помножений на 6 добуток квадрату першого та квадрату другого виразу відняти помножений на 4 добуток першого та кубу другого виразу додати в четвертому степені другий вираз.<br> <br> <br> <br>квадрат суми трьох виразів дорівнює квадрат першого виразу додати квадрат другого виразу додати квадрат третього виразу додати подвоєний добуток першого та другого виразу додати подвоєний добуток першого та третього виразу додати подвоєний добуток другого та третього виразу.<br> <br>квадрат різниці трьох виразів дорівнює квадрат першого виразу додати квадрат другого виразу додати квадрат третього виразу відняти подвоєний добуток першого та другого виразу відняти подвоєний добуток першого та третього виразу додати подвоєний добуток другого та третього виразу.<br><br><br>Відмітимо, що всі ці формули – тотожності: вони правильні для будь-яких значень.<br><br>http://www.youtube.com/watch?v=yn8SLQzYx-I<br><br><br><br> <br><br>Перевір себе!<br>1. З написаних виразів складіть формули скороченого множення:<br>Виберіть у правій колонці формулу і сформулюйте правила, що відповідають даним формулам. <br>Квадрат суми<br>Квадрат різниці <br>Різниця квадратів <br>Куб суми <br>Куб різниці <br> <br>а2 – b2<br>( а + b)2<br>( а - b)3<br>( а - b)2<br>( а + b)3<br>а2 – 2а b + b2<br>( а – b)(а + b)<br>а2 + 2а b + b2<br>( а + b)( а2 – 2а b + b2)<br>( а - b)( а2 + 2а b + b2)<br><br><br>Кубу першого виразу, плюс потроєний добуток квадрата першого виразу на другий, плюс потроєний добуток першого на квадрат другого, плюс куб другого виразу. <br>Добутку їх суми на різницю.<br>Квадрату першого члена плюс подвоєний добуток першого на другий, плюс квадрат другого члена<br>Квадрату першого члена мінус подвоєний добуток першого на другий, плюс квадрат другого члена.<br>Кубу першого виразу, мінус потроєний добуток квадрата першого виразу на другий, плюс потроєний добуток першого на квадрат другого, мінус куб другого виразу. <br><br> <br><br>Список використаної літератури:<br>1. Урок на тему «Тотожні вирази» викладача Конченко Т. М. , Гімназії міжнародних відносин, м. Київ (СЗШ №323).<br>2. Урок на тему «Перетворення тотожних виразів» викладача Конченко Т. М. , Гімназії міжнародних відносин, м. Київ (СЗШ №323).<br>3. Істер О. А. «Алгебра. 7 клас».<br>4. Мерзляк А. Г., Полонський В. Б., Рабінович Ю. М., ЯкірМ. С. Збірник задачізавдань для тематичного оцінювання з алгебри для 7 класу. – Харків, Гімназія, 2004. – 112 с.: іл.<br><br><br> |
| | | | |
| | <br> | | <br> |
Версия 07:29, 18 января 2011
Гіпермаркет Знань>>Математика>>Математика 7 клас. Повні уроки>> АЛГЕБРА: Тотожні вирази. Тотожні перетворення виразів. Повні уроки
АЛГЕБРА
Тема 6. Тотожні вирази. Тотожні перетворення виразів
Мета: зрозуміти, що таке тотожності. Дізнатися, які вирази є тотожно рівними. Згадати формули скороченого множення. Дізнатися,що таке умовні тотожності.
1. Тотожнорівні вирази. Тотожне перетворення виразу.
2. Умовні тотожності.
1. Тотожнорівні вирази. Тотожне перетворення виразу
Розглянемо 2 приклада: х2-2х і 4х-5. При х=2 маємо: 2*2-2*2=0 і 4*2-5=3. Числа 0 та 3 називаються відповідними значеннями виразів х2-2х і 4х-5 при х=2. Знайдемо значення цих виразів при х=1. Маємо:
1*1-2*1=-1 і 4*1-5=-1.
Відповідні значення двох виразів можуть бути однаковими,а можуть і відрізнятися. Якщо значення рівні,то вирази назіваються тотожними.
Два вирази називаються тотожно рівними, якщо при будь-яких допустимих значеннях букв відповідні значення цих виразів дорівнюють одне одному.
Рівність, яка є правильною при будь-яких значеннях букв, називається тотожністю.
Заміна виразу тотожно рівним йому виразом називається тотожним перетворенням виразу.
Приклади тотожностей:
1) a+b=b+a
2) a+0=a
3) 3a+5a-7=8а-5-2.
А ось 4а-3с+1=2а+5с-2 не є тотожністю,бо ,наприклад, при а=1 та с=0 вони не дорівнюють один одному.
Тотожне перетворення алгебраїчного виразу – заміна цього виразу іншим, тотожно рівним йому.
Спростити алгебраїчний вираз – означає замінити його на тотожно рівний, але найпростіший за записом. Як видно з означення, спрощення алгебраїчного виразу є тотожним перетворенням. Розглянемо приклад спрощення.
1. Спростити вираз (x-y)(x+2y)-x2+2y2.
(x-y)(x+2y)-x2+2y2=x*x+2xy-xy-2y*y-x2+2y2=xy.
З деякими видами тотожних перетворень ви уже знайомі: розкриття дужок і, навпаки, винесення спільного множника за дужки; множення чисельника і знаменника дробу на одне й те ж саме число, що не дорівнює 0 – все це тотожні перетворення.
При проведенні тотожних перетворень часто стають корисними формули скороченого множення. Основні з них:
Пишеться
| Читається
|
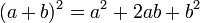
| квадрат суми двох виразів дорівнює квадрат першого виразу додати подвоєний добуток цих виразів додати квадрат другого виразу.
|
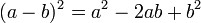
| квадрат різниці двох виразів дорівнює квадрат першого виразу відняти подвоєний добуток цих виразів додати квадрат другого виразу.
|
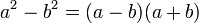
| різниця квадратів двох виразів дорівнює добутку різниці та суми цих виразів.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
куб суми двох виразів дорівнює куб першого виразу додати потроєний добуток квадрату першого та другого виразу додати потроєний добуток першого та квадрату другого виразу додати куб другого виразу.
куб різниці двох виразів = куб першого виразу відняти потроєний добуток квадрату першого та другого виразу додати потроєний добуток першого та квадрату другого виразу відняти куб другого виразу.
сума кубів двох виразів дорівнює добутку суми цих виразів та неповному квадрату різниці цих виразів (квадрат першого виразу відняти добуток цих виразів додати квадрат другого виразу).
різниця кубів двох виразів дорівнює добутку різниці цих виразів та неповному квадрату суми цих виразів ( квадрат першого виразу додати добуток цих виразів додати квадрат другого виразу).
в четвертому степені сума двох виразів дорівнює в четвертому степені перший вираз додати помножений на 4 добуток кубу першого та другого виразу додати помножений на 6 добуток квадрату першого та квадрату другого виразу додати помножений на 4 добуток першого та кубу другого виразу додати в четвертому степені другий вираз.
в четвертому степені різниця двох виразів дорівнює в четвертому степені перший вираз відняти помножений на 4 добуток кубу першого та другого виразу додати помножений на 6 добуток квадрату першого та квадрату другого виразу відняти помножений на 4 добуток першого та кубу другого виразу додати в четвертому степені другий вираз.
квадрат суми трьох виразів дорівнює квадрат першого виразу додати квадрат другого виразу додати квадрат третього виразу додати подвоєний добуток першого та другого виразу додати подвоєний добуток першого та третього виразу додати подвоєний добуток другого та третього виразу.
квадрат різниці трьох виразів дорівнює квадрат першого виразу додати квадрат другого виразу додати квадрат третього виразу відняти подвоєний добуток першого та другого виразу відняти подвоєний добуток першого та третього виразу додати подвоєний добуток другого та третього виразу.
Відмітимо, що всі ці формули – тотожності: вони правильні для будь-яких значень.
http://www.youtube.com/watch?v=yn8SLQzYx-I
Перевір себе!
1. З написаних виразів складіть формули скороченого множення:
Виберіть у правій колонці формулу і сформулюйте правила, що відповідають даним формулам.
Квадрат суми
Квадрат різниці
Різниця квадратів
Куб суми
Куб різниці
а2 – b2
( а + b)2
( а - b)3
( а - b)2
( а + b)3
а2 – 2а b + b2
( а – b)(а + b)
а2 + 2а b + b2
( а + b)( а2 – 2а b + b2)
( а - b)( а2 + 2а b + b2)
Кубу першого виразу, плюс потроєний добуток квадрата першого виразу на другий, плюс потроєний добуток першого на квадрат другого, плюс куб другого виразу.
Добутку їх суми на різницю.
Квадрату першого члена плюс подвоєний добуток першого на другий, плюс квадрат другого члена
Квадрату першого члена мінус подвоєний добуток першого на другий, плюс квадрат другого члена.
Кубу першого виразу, мінус потроєний добуток квадрата першого виразу на другий, плюс потроєний добуток першого на квадрат другого, мінус куб другого виразу.
Список використаної літератури:
1. Урок на тему «Тотожні вирази» викладача Конченко Т. М. , Гімназії міжнародних відносин, м. Київ (СЗШ №323).
2. Урок на тему «Перетворення тотожних виразів» викладача Конченко Т. М. , Гімназії міжнародних відносин, м. Київ (СЗШ №323).
3. Істер О. А. «Алгебра. 7 клас».
4. Мерзляк А. Г., Полонський В. Б., Рабінович Ю. М., ЯкірМ. С. Збірник задачізавдань для тематичного оцінювання з алгебри для 7 класу. – Харків, Гімназія, 2004. – 112 с.: іл.
Відредаговано і надіслано Мазуренко М.С.
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
Предмети > Математика > Математика 7 клас
|










