|
|
|
| Строка 11: |
Строка 11: |
| | <br> | | <br> |
| | | | |
| - | <br> 22. Графік функції<br><br>Мета: навчитися будувати графіки функції.<br><br>Графіком функції y = f(x) називається множина всіх точок координатної площини (x, f(x)), у яких абсциси належать області визначення функції, а ординати дорівнюють відповідним значенням функції.<br><br> <br> <br>Функцію y = f(x) називають парною, якщо для деяких значень x і (-x) з її області визначення виконується рівність f(x) = f(-x). <br> <br>Функцію y = f(x) називають непарною, якщо для деяких значень x і (-x) з її області визначення виконується рівність f(-x) = -f(x). <br> <br>Функцію y = f(x) називають зростаючою, якщо більшому значенню аргументу x відповідає більше значення функції y = f(x). <br> <br>Функцію y = f(x) називають спадною, якщо більшому значенню аргументу x відповідає менше значення функції y = f(x). <br> <br>Функцію y = f(x) називають періодичною з періодом T, якщо для будь-яких x, x + T, x - T виконується рівність f(x) = f(x + T) = f(x - T). <br> <br>Якщо в формулі y = f(x) поміняти місцями x і y, то одержимо нову функцію g(x), обернену до даної. Наприклад, оберненою до функції y = 3x - 1 є функція y = (x + 1)/3 . Графіки даної функції і функції оберненої до даної симетричні відносно прямої y = x. <br>Якщо при деякому x функція y = f(x) набуває найбільшого значення, то цю точку називають точкою максимуму цієї функції і позначають xmax. <br>Якщо в точці x = x0 функція y = f(x) набуває найменшого значення, то цю точку називають точкою мінімуму функції і позначають xmin. <br>Точки максимуму і точки мінімуму називають точками екстремуму функції. Значення функції в цих точках позначають ymax і ymin. <br>Основні елементарні функції <br> <br>Лінійна функція має вид <br>і її графіком є пряма лінія. Функція ні парна, ні непарна. <br>Число <br>називають кутовим коефіцієнтом прямої. <br> <br>Квадратична функція має вид <br> <br>Її графіком є парабола з вершиною в точці з координатами: <br> <br> <br>Показникова функція має вид <br> <br>При a > 1 функція зростаюча, а при a < 1 - спадна. <br><br> <br> <br> <br><br><br>http://www.youtube.com/watch?v=E6SxdbKP3E4<br><br><br>Самостійна робота:<br><br>1. Побудувати графік рівняння:<br><br>1) х-у=2;<br>2) 3х+4у=6;<br>3) х-5у=4;<br>4) 3х+2у=6;<br>5) 2х-у=5;<br>6)4х+3у=12;<br>7)12у-х=4.<br><br><br><br>Список використаної літератури:<br>1. Урок на тему «Графіки фукнцій» викладача Конченко Т. М. , Гімназії міжнародних відносин, м. Київ (СЗШ №323).<br>2. Істер О. А. «Алгебра. 7 клас».<br>3. Мерзляк А. Г., Полонський В. Б., Рабінович Ю. М., ЯкірМ. С. Збірник задачізавдань для тематичного оцінювання з алгебри для 7 класу. – Харків, Гімназія, 2004. – 112 с.: іл.<br><br><br> | + | <br> <u>'''Мета:'''</u> навчитися будувати графіки функції.<br><br>'''Графіком функції''' y = f(x) називається множина всіх точок координатної площини (x, f(x)), у яких абсциси належать області визначення функції, а ординати дорівнюють відповідним значенням функції.<br><br> |
| | + | |
| | + | {| cellspacing="1" cellpadding="1" border="1" style="width: 855px; height: 108px;" |
| | + | |- |
| | + | | [[Image:1901-31.jpg]] |
| | + | | Функцію y = f(x) називають '''парною''', якщо для деяких значень x і (-x) з її області визначення виконується рівність f(x) = f(-x). |
| | + | |- |
| | + | | [[Image:1901-32.jpg]] |
| | + | | Функцію y = f(x) називають '''непарною''', якщо для деяких значень x і (-x) з її області визначення виконується рівність f(-x) = -f(x). |
| | + | |- |
| | + | | |
| | + | | Функцію y = f(x) називають '''зростаючою''', якщо більшому значенню аргументу x відповідає більше значення функції y = f(x). |
| | + | |- |
| | + | | |
| | + | | Функцію y = f(x) називають '''спадною''', якщо більшому значенню аргументу x відповідає менше значення функції y = f(x). |
| | + | |- |
| | + | | |
| | + | | Функцію y = f(x) називають '''періодичною з періодом T,''' якщо для будь-яких x, x + T, x - T виконується рівність f(x) = f(x + T) = f(x - T). |
| | + | |- |
| | + | | |
| | + | | Якщо в формулі y = f(x) поміняти місцями x і y, то одержимо нову функцію g(x), '''обернену''' до даної. Наприклад, оберненою до функції y = 3x - 1 є функція y = (x + 1)/3 . Графіки даної функції і функції оберненої до даної симетричні відносно прямої y = x. |
| | + | |} |
| | + | |
| | + | <br> <br> <br> <br><br> <br> <br><br> <br> |
| | + | |
| | + | <br>Якщо при деякому x функція y = f(x) набуває найбільшого значення, то цю точку називають точкою максимуму цієї функції і позначають xmax. <br>Якщо в точці x = x0 функція y = f(x) набуває найменшого значення, то цю точку називають точкою мінімуму функції і позначають xmin. <br>Точки максимуму і точки мінімуму називають точками екстремуму функції. Значення функції в цих точках позначають ymax і ymin. <br>Основні елементарні функції <br> <br>Лінійна функція має вид <br>і її графіком є пряма лінія. Функція ні парна, ні непарна. <br>Число <br>називають кутовим коефіцієнтом прямої. <br> <br>Квадратична функція має вид <br> <br>Її графіком є парабола з вершиною в точці з координатами: <br> <br> <br>Показникова функція має вид <br> <br>При a > 1 функція зростаюча, а при a < 1 - спадна. <br><br> <br> <br> <br><br><br>http://www.youtube.com/watch?v=E6SxdbKP3E4<br><br><br>Самостійна робота:<br><br>1. Побудувати графік рівняння:<br><br>1) х-у=2;<br>2) 3х+4у=6;<br>3) х-5у=4;<br>4) 3х+2у=6;<br>5) 2х-у=5;<br>6)4х+3у=12;<br>7)12у-х=4.<br><br><br><br>Список використаної літератури:<br>1. Урок на тему «Графіки фукнцій» викладача Конченко Т. М. , Гімназії міжнародних відносин, м. Київ (СЗШ №323).<br>2. Істер О. А. «Алгебра. 7 клас».<br>3. Мерзляк А. Г., Полонський В. Б., Рабінович Ю. М., ЯкірМ. С. Збірник задачізавдань для тематичного оцінювання з алгебри для 7 класу. – Харків, Гімназія, 2004. – 112 с.: іл.<br><br><br> |
| | | | |
| | <br> | | <br> |
Версия 13:41, 19 января 2011
Гіпермаркет Знань>>Математика>>Математика 7 клас. Повні уроки>> АЛГЕБРА: Графік функції
АЛГЕБРА
Тема 22. Графік функції
Мета: навчитися будувати графіки функції.
Графіком функції y = f(x) називається множина всіх точок координатної площини (x, f(x)), у яких абсциси належать області визначення функції, а ординати дорівнюють відповідним значенням функції.
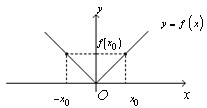
| Функцію y = f(x) називають парною, якщо для деяких значень x і (-x) з її області визначення виконується рівність f(x) = f(-x).
|
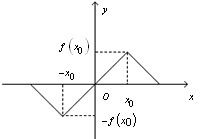
| Функцію y = f(x) називають непарною, якщо для деяких значень x і (-x) з її області визначення виконується рівність f(-x) = -f(x).
|
|
| Функцію y = f(x) називають зростаючою, якщо більшому значенню аргументу x відповідає більше значення функції y = f(x).
|
|
| Функцію y = f(x) називають спадною, якщо більшому значенню аргументу x відповідає менше значення функції y = f(x).
|
|
| Функцію y = f(x) називають періодичною з періодом T, якщо для будь-яких x, x + T, x - T виконується рівність f(x) = f(x + T) = f(x - T).
|
|
| Якщо в формулі y = f(x) поміняти місцями x і y, то одержимо нову функцію g(x), обернену до даної. Наприклад, оберненою до функції y = 3x - 1 є функція y = (x + 1)/3 . Графіки даної функції і функції оберненої до даної симетричні відносно прямої y = x.
|
Якщо при деякому x функція y = f(x) набуває найбільшого значення, то цю точку називають точкою максимуму цієї функції і позначають xmax.
Якщо в точці x = x0 функція y = f(x) набуває найменшого значення, то цю точку називають точкою мінімуму функції і позначають xmin.
Точки максимуму і точки мінімуму називають точками екстремуму функції. Значення функції в цих точках позначають ymax і ymin.
Основні елементарні функції
Лінійна функція має вид
і її графіком є пряма лінія. Функція ні парна, ні непарна.
Число
називають кутовим коефіцієнтом прямої.
Квадратична функція має вид
Її графіком є парабола з вершиною в точці з координатами:
Показникова функція має вид
При a > 1 функція зростаюча, а при a < 1 - спадна.
http://www.youtube.com/watch?v=E6SxdbKP3E4
Самостійна робота:
1. Побудувати графік рівняння:
1) х-у=2;
2) 3х+4у=6;
3) х-5у=4;
4) 3х+2у=6;
5) 2х-у=5;
6)4х+3у=12;
7)12у-х=4.
Список використаної літератури:
1. Урок на тему «Графіки фукнцій» викладача Конченко Т. М. , Гімназії міжнародних відносин, м. Київ (СЗШ №323).
2. Істер О. А. «Алгебра. 7 клас».
3. Мерзляк А. Г., Полонський В. Б., Рабінович Ю. М., ЯкірМ. С. Збірник задачізавдань для тематичного оцінювання з алгебри для 7 класу. – Харків, Гімназія, 2004. – 112 с.: іл.
Відредаговано і надіслано Мазуренко М.С.
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
Предмети > Математика > Математика 7 клас
|












