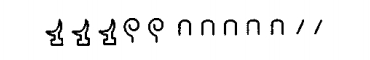|
|
|
| Строка 5: |
Строка 5: |
| | <br> '''<br>''' | | <br> '''<br>''' |
| | | | |
| - | ''' § 4.2. Обозначение чисел и счет в Древнем Египте'''<br><br>Примерно в третьем тысячелетии до нашей эры египтяне придумали свою '''[[Путешествие в историю чисел|числовую систему]]''', в которой для обозначения ключевых чисел 1, 10, 100 и так далее использовались специальные значки — иероглифы. Вот они; <br><br>[[Image:15-03-054.jpg]]<br> <br>С течением времени эти знаки изменились и приобрели более простой вид:<br><br>[[Image:15-03-055.jpg]]<br> <br>Все остальные числа составлялись из этих ключевых символов при помощи операции сложения. Например, чтобы изобразить 3 252, рисовали три цветка лотоса (три тысячи), два свернутых пальмовых листа (две сотни), пять дуг (пять десятков) и два шеста (две единицы):<br><br>[[Image:15-03-056.jpg]]<br><br>Величина числа не зависела от того, в каком порядке располагались составляющие его знаки: их можно было записывать сверху вниз, справа налево или вперемешку. | + | ''' § 4.2. Обозначение чисел и счет ''' |
| | + | |
| | + | ''' в Древнем Египте'''<br><br>Примерно в третьем тысячелетии до нашей эры египтяне придумали свою '''[[Путешествие в историю чисел|числовую систему]]''', в которой для обозначения ключевых чисел 1, 10, 100 и так далее использовались специальные значки — иероглифы. Вот они; <br><br>[[Image:15-03-054.jpg|550px|Иероглифы]]<br> <br>С течением времени эти знаки изменились и приобрели более простой вид:<br><br>[[Image:15-03-055.jpg|550px|Иероглифы]]<br> <br>Все остальные числа составлялись из этих ключевых символов при помощи операции сложения. Например, чтобы изобразить 3 252, рисовали три цветка лотоса (три тысячи), два свернутых пальмовых листа (две сотни), пять дуг (пять десятков) и два шеста (две единицы):<br><br>[[Image:15-03-056.jpg|550px|Иероглифы]]<br><br>Величина числа не зависела от того, в каком порядке располагались составляющие его знаки: их можно было записывать сверху вниз, справа налево или вперемешку. |
| | | | |
| | Система счисления называется не'''[[Позиционные системы счисления|позиционной]]''', если в ней количественные значения символов, используемых для записи чисел, не зависят от их положения (места, позиции) в коде числа. | | Система счисления называется не'''[[Позиционные системы счисления|позиционной]]''', если в ней количественные значения символов, используемых для записи чисел, не зависят от их положения (места, позиции) в коде числа. |
| Строка 11: |
Строка 13: |
| | '''[[Другие позиционные системы счисления|Система счисления]]''' Древнего Египта является непозиционной. Особую роль у египтян играло число 2 и его степени. Умножение и деление они проводили путем последовательного удвоения и сложения чисел. Выглядели такие расчеты довольно громоздко. | | '''[[Другие позиционные системы счисления|Система счисления]]''' Древнего Египта является непозиционной. Особую роль у египтян играло число 2 и его степени. Умножение и деление они проводили путем последовательного удвоения и сложения чисел. Выглядели такие расчеты довольно громоздко. |
| | | | |
| - | Например, чтобы умножить 15 на 24, составляли следующую таблицу:<br><br>[[Image:15-03-057.jpg]]<br><br>Здесь в левом столбце записаны результаты удвоений единицы, а в правом — числа 24. Записи делались до тех пор, пока не оказывалось, что из чисел левого столбца можно составить множитель 15:1 + 2 + 4 + 1 + 8 = 15. После этого складывались соответствующие числа правого столбца: <br><br>24 + 48 + 96 + 192 = 360.<br><br>При делении египтяне многократно удваивали в правом столбце делитель и, соответственно, в левом столбце — число 1, пока числа правого столбца оставались не большими делимого. Далее из чисел правого столбца пытались составить делимое, и если это удавалось, то сумма соответствующих чисел в левом столбце давала искомое частное, Если делимое не делилось нацело на делитель, то получали частное и остаток. | + | Например, чтобы умножить 15 на 24, составляли следующую таблицу:<br><br>[[Image:15-03-057.jpg|240px|Таблица]]<br><br>Здесь в левом столбце записаны результаты удвоений единицы, а в правом — числа 24. Записи делались до тех пор, пока не оказывалось, что из чисел левого столбца можно составить множитель 15:1 + 2 + 4 + 1 + 8 = 15. После этого складывались соответствующие числа правого столбца: <br><br>24 + 48 + 96 + 192 = 360.<br><br>При делении египтяне многократно удваивали в правом столбце делитель и, соответственно, в левом столбце — число 1, пока числа правого столбца оставались не большими делимого. Далее из чисел правого столбца пытались составить делимое, и если это удавалось, то сумма соответствующих чисел в левом столбце давала искомое частное, Если делимое не делилось нацело на делитель, то получали частное и остаток. |
| | | | |
| - | Например, чтобы разделить 541 на 12, надо было составить таблицу:<br><br>[[Image:15-03-058.jpg]]<br><br>541 = 384 + 96 + 48 + 12 + 1; <br>32 + 8 + 4 + 1 = 45.<br><br>Таким образом, при делении 541 на 12 получаем частное 45 и остаток 1.<br><br><br> | + | Например, чтобы разделить 541 на 12, надо было составить таблицу:<br><br>[[Image:15-03-058.jpg|240px|Таблица]]<br><br>541 = 384 + 96 + 48 + 12 + 1; <br>32 + 8 + 4 + 1 = 45.<br><br>Таким образом, при делении 541 на 12 получаем частное 45 и остаток 1.<br><br><br> |
| | | | |
| | ''Босова Л. Л. Информатика: Учебник для 6 класса / Л. Л. Босова. — 3-е изд., испр. и доп. — М.: БИНОМ. Лаборатория знаний, 2005. — 208 с.: ил.'' | | ''Босова Л. Л. Информатика: Учебник для 6 класса / Л. Л. Босова. — 3-е изд., испр. и доп. — М.: БИНОМ. Лаборатория знаний, 2005. — 208 с.: ил.'' |
Версия 13:47, 27 июня 2012
Гипермаркет знаний>>Информатика >>Информатика 6 класс>> Обозначение чисел и счет в Древнем Египте
§ 4.2. Обозначение чисел и счет
в Древнем Египте
Примерно в третьем тысячелетии до нашей эры египтяне придумали свою числовую систему, в которой для обозначения ключевых чисел 1, 10, 100 и так далее использовались специальные значки — иероглифы. Вот они;

С течением времени эти знаки изменились и приобрели более простой вид:

Все остальные числа составлялись из этих ключевых символов при помощи операции сложения. Например, чтобы изобразить 3 252, рисовали три цветка лотоса (три тысячи), два свернутых пальмовых листа (две сотни), пять дуг (пять десятков) и два шеста (две единицы):
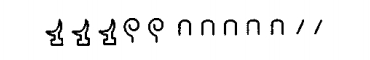
Величина числа не зависела от того, в каком порядке располагались составляющие его знаки: их можно было записывать сверху вниз, справа налево или вперемешку.
Система счисления называется непозиционной, если в ней количественные значения символов, используемых для записи чисел, не зависят от их положения (места, позиции) в коде числа.
Система счисления Древнего Египта является непозиционной. Особую роль у египтян играло число 2 и его степени. Умножение и деление они проводили путем последовательного удвоения и сложения чисел. Выглядели такие расчеты довольно громоздко.
Например, чтобы умножить 15 на 24, составляли следующую таблицу:

Здесь в левом столбце записаны результаты удвоений единицы, а в правом — числа 24. Записи делались до тех пор, пока не оказывалось, что из чисел левого столбца можно составить множитель 15:1 + 2 + 4 + 1 + 8 = 15. После этого складывались соответствующие числа правого столбца:
24 + 48 + 96 + 192 = 360.
При делении египтяне многократно удваивали в правом столбце делитель и, соответственно, в левом столбце — число 1, пока числа правого столбца оставались не большими делимого. Далее из чисел правого столбца пытались составить делимое, и если это удавалось, то сумма соответствующих чисел в левом столбце давала искомое частное, Если делимое не делилось нацело на делитель, то получали частное и остаток.
Например, чтобы разделить 541 на 12, надо было составить таблицу:
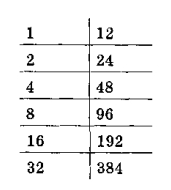
541 = 384 + 96 + 48 + 12 + 1;
32 + 8 + 4 + 1 = 45.
Таким образом, при делении 541 на 12 получаем частное 45 и остаток 1.
Босова Л. Л. Информатика: Учебник для 6 класса / Л. Л. Босова. — 3-е изд., испр. и доп. — М.: БИНОМ. Лаборатория знаний, 2005. — 208 с.: ил.
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|