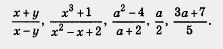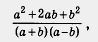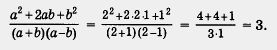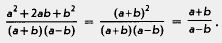|
|
|
| Строка 7: |
Строка 7: |
| | <br> | | <br> |
| | | | |
| - | Понятие алгебраической дроби знакомо вам из курса алгебры 7-го класса, где мы довольно много внимания уделили сокращению алгебраических дробей. Теперь настало время специально заняться изучением этого непростого раздела алгебры. | + | Понятие алгебраической дроби знакомо вам из [http://xvatit.com/vuzi/ '''курса'''] алгебры 7-го класса, где мы довольно много внимания уделили сокращению алгебраических дробей. Теперь настало время специально заняться изучением этого непростого раздела алгебры. |
| | | | |
| | Определение. Алгебраической дробью называют выражение [[Image:11-06-1.jpg]] , где Р и Q — многочлены; Р — числитель алгебраической дроби, Q — знаменатель алгебраической дроби. | | Определение. Алгебраической дробью называют выражение [[Image:11-06-1.jpg]] , где Р и Q — многочлены; Р — числитель алгебраической дроби, Q — знаменатель алгебраической дроби. |
| Строка 53: |
Строка 53: |
| | Итак, теперь вы не сомневаетесь в том, что алгебраические дроби нужны и что мы должны научиться оперировать с ними. Этим и займемся в следующих параграфах. | | Итак, теперь вы не сомневаетесь в том, что алгебраические дроби нужны и что мы должны научиться оперировать с ними. Этим и займемся в следующих параграфах. |
| | | | |
| - | | + | <br> |
| | | | |
| | ''Мордкович А. Г., Алгебра. 8 кл.: Учеб. для общеобразоват. учреждений.— 3-е изд., доработ. — М.: Мнемозина, 2001. — 223 с: ил. ''<br> | | ''Мордкович А. Г., Алгебра. 8 кл.: Учеб. для общеобразоват. учреждений.— 3-е изд., доработ. — М.: Мнемозина, 2001. — 223 с: ил. ''<br> |
| | | | |
| - | | + | <br> |
| | | | |
| | <sub>Материалы по математике [[Гипермаркет знаний - первый в мире!|онлайн]], задачи и ответы по классам, планы конспектов уроков по математике [[Математика|скачать]]</sub> | | <sub>Материалы по математике [[Гипермаркет знаний - первый в мире!|онлайн]], задачи и ответы по классам, планы конспектов уроков по математике [[Математика|скачать]]</sub> |
Версия 19:46, 7 октября 2012
Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика:Основные понятия-1
Основные понятия
Понятие алгебраической дроби знакомо вам из курса алгебры 7-го класса, где мы довольно много внимания уделили сокращению алгебраических дробей. Теперь настало время специально заняться изучением этого непростого раздела алгебры.
Определение. Алгебраической дробью называют выражение 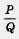 , где Р и Q — многочлены; Р — числитель алгебраической дроби, Q — знаменатель алгебраической дроби. , где Р и Q — многочлены; Р — числитель алгебраической дроби, Q — знаменатель алгебраической дроби.
Примеры алгебраических дробей:
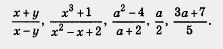
Иногда алгебраическое выражение по форме является алгебраической дробью, а по существу — нет. Так обстоит дело в последних двух из пяти приведенных выше примеров. Действительно, 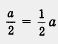 — это одночлен (с коэффициентом — — это одночлен (с коэффициентом — 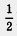 ); дробь ); дробь 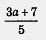 можно переписать в виде можно переписать в виде 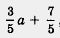 ,а это уже не алгебраическая дробь, а многочлен (двучлен). Да и в третьем из приведенных примеров после сокращения получается не дробь, а двучлен а - 2. Но, в сущности, это не столь важно, так было и с обыкновенными дробями. Скажем, ,а это уже не алгебраическая дробь, а многочлен (двучлен). Да и в третьем из приведенных примеров после сокращения получается не дробь, а двучлен а - 2. Но, в сущности, это не столь важно, так было и с обыкновенными дробями. Скажем, 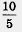 по форме — обыкновенная дробь, а по содержанию — натуральное число 2. по форме — обыкновенная дробь, а по содержанию — натуральное число 2.
Пример 1. Найти значение алгебраической дроби
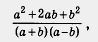
если: а) а = 2, b = 1; б) а = 5, b = 0; в) а = 4, b = 4.
Решение. а) При а = 2, b = 1 получаем
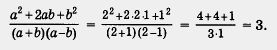
б) При а = 5, b = 0 получаем
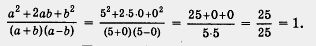
в) При а = 4, b = 4 выражение а - b обращается в нуль, а потому знаменатель данной дроби обращается в нуль. Но на нуль делить нельзя. Значит, пара значений а = 4, b = 4 является для заданной дроби недопустимой, т. е. числитель алгебраическая дробь в этом случае не имеет знаменатель смысла.
Условимся в дальнейшем, что переменные, входящие в состав алгебраической дроби, принимают лишь допустимые значения, т. е. такие значения, при которых знаменатель дроби не обращается в нуль.
Замечание. Пример 1 решен правильно, но «некупьтурно». Ведь апгебраическую дробь , 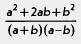 — можно сократить. Напомним, как мы это делали в 7-м классе: — можно сократить. Напомним, как мы это делали в 7-м классе:
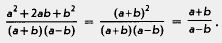
Согласитесь, что если бы мы начали с сокращения дроби, то все вычисления существенно упростились. Поэтому у математиков как бы выработался рефпекс: если им встретилась алгебраическая дробь, то прежде всего они выясняют, нельзя пи ее сократить.
Пример 2. Лодка прошла 10 км по течению реки и 6 км против течения, затратив на весь путь 2 ч. Чему равна собственная скорость лодки, если скорость течения реки равна 2 км/ч?
Решение.
Первый этап. Составление математической модели. Пусть х км/ч — собственная скорость лодки, тогда по течению реки она плывет со скоростью (х + 2) км/ч, а против течения — со скоростью (х - 2) км/ч.
По течению реки, т. е. со скоростью (х + 2) км/ч, лодка прошла путь 10 км. Значит, время, затраченное на этот путь, выражается формулой —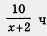 . .
Против течения реки, т. е. со скоростью (х - 2) км/ч, лодка прошла путь 6 км. Следовательно, время, затраченное на этот путь, выражается формулой —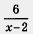 . .
По условию задачи на весь путь (т. е. на 10 км по течению и 6 км против течения) суммарно затрачено 2 ч. Итак, получаем 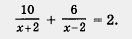
Это уравнение — математическая модель задачи.
Второй этап. Работа с составленной моделью. Обратите внимание на левую часть уравнения. Она представляет собой сумму алгебраических дробей. Таким образом, приходим к следующим выводам:
1) алгебраические дроби могут входить в состав той или иной математической модели;
2) надо научиться оперировать с алгебраическими дробями, чтобы, в частности, уметь складывать дроби
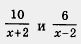 ; ;
3) пока мы не научимся оперировать с алгебраическими дробями, мы не сможем осуществить второй этап решения задачи — этап работы с составленной моделью.
Придется нам вернуться к этой задаче позднее, когда мы будем готовы довести ее до конца, — это произойдет в § 7.
Итак, теперь вы не сомневаетесь в том, что алгебраические дроби нужны и что мы должны научиться оперировать с ними. Этим и займемся в следующих параграфах.
Мордкович А. Г., Алгебра. 8 кл.: Учеб. для общеобразоват. учреждений.— 3-е изд., доработ. — М.: Мнемозина, 2001. — 223 с: ил.
Материалы по математике онлайн, задачи и ответы по классам, планы конспектов уроков по математике скачать
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|