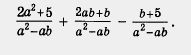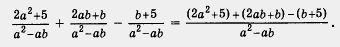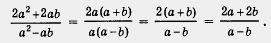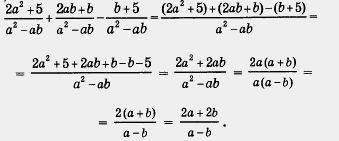|
|
|
| Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Сложение, вычитание алгебраических дробей с одинаковыми знаменателями </metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Сложение, вычитание алгебраических дробей с одинаковыми знаменателями, обыкновенные дроби, алгебраическую дробь, преобразований</metakeywords> |
| | | | |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика:Сложение и вычитание алгебраических дробей с одинаковыми знаменателями'''<br> | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика:Сложение и вычитание алгебраических дробей с одинаковыми знаменателями'''<br> |
| Строка 7: |
Строка 7: |
| | '''Сложение и вычитание алгебраических дробей с одинаковыми знаменателями'''<br> | | '''Сложение и вычитание алгебраических дробей с одинаковыми знаменателями'''<br> |
| | | | |
| - | <br>Алгебраические дроби с одинаковыми знаменателями складывают и вычитают по тому же правилу, что и обыкновенные дроби: | + | <br>Алгебраические дроби с одинаковыми знаменателями складывают и вычитают по тому же правилу, что и '''[[Задачі до уроку «Додавання і віднімання звичайних дробів з однаковими знаменниками.»|обыкновенные дроби]]''': |
| | | | |
| | [[Image:11-06-28.jpg|180px|Задание]]<br><br>т. е. составляют соответствующую алгебраическую [http://xvatit.com/busines/ '''сумму'''] числителей, а знаменатель оставляют без изменений. | | [[Image:11-06-28.jpg|180px|Задание]]<br><br>т. е. составляют соответствующую алгебраическую [http://xvatit.com/busines/ '''сумму'''] числителей, а знаменатель оставляют без изменений. |
| Строка 19: |
Строка 19: |
| | (2а<sup>2</sup> + 5) +(2аb + b) - (b + 5) = <br>= 2а<sup>2</sup> + 5 + 2аb + b - b - 5 = 2а<sup>2</sup> + 2аb. | | (2а<sup>2</sup> + 5) +(2аb + b) - (b + 5) = <br>= 2а<sup>2</sup> + 5 + 2аb + b - b - 5 = 2а<sup>2</sup> + 2аb. |
| | | | |
| - | Таким образом, заданную алгебраическую сумму трех дробей нам удалось преобразовать в дробь —[[Image:11-06-31.jpg|Задание]] . <br>А теперь вспомните то, что мы говорили в предыдущем параграфе: получив алгебраическую дробь, нужно посмотреть, нельзя ли ее сократить. | + | Таким образом, заданную алгебраическую сумму трех дробей нам удалось преобразовать в дробь —[[Image:11-06-31.jpg|Задание]] . <br>А теперь вспомните то, что мы говорили в предыдущем параграфе: получив '''[[Упражнения: Основные понятия-1 (8 класс)|алгебраическую дробь]]''', нужно посмотреть, нельзя ли ее сократить. |
| | | | |
| | Имеем | | Имеем |
| Строка 25: |
Строка 25: |
| | [[Image:11-06-32.jpg|320px|Задание]]<br><br>Приведем теперь решение рассмотренного примера без комментариев (как это вы будете делать у себя в тетрадях): | | [[Image:11-06-32.jpg|320px|Задание]]<br><br>Приведем теперь решение рассмотренного примера без комментариев (как это вы будете делать у себя в тетрадях): |
| | | | |
| - | [[Image:11-06-33.jpg|420px|Задание]]<br><br>Как видите, в результате преобразований получилось более простое алгебраическое выражение, чем было задано в условии примера. Именно в упрощении и состоит цель преобразований, поэтому часто, вместо словосочетания «выполнить действия», используют словосочетание «упростить выражение». | + | [[Image:11-06-33.jpg|420px|Задание]]<br><br>Как видите, в результате '''[[Преобразование рациональных выражений|преобразований]]''' получилось более простое алгебраическое выражение, чем было задано в условии примера. Именно в упрощении и состоит цель преобразований, поэтому часто, вместо словосочетания «выполнить действия», используют словосочетание «упростить выражение». |
| | | | |
| | ''<br>Мордкович А. Г., Алгебра. 8 кл.: Учеб. для общеобразоват. учреждений.— 3-е изд., доработ. — М.: Мнемозина, 2001. — 223 с: ил. ''<br><br><sub>Планирование уроков по математике [[Гипермаркет знаний - первый в мире!|онлайн]], задачи и ответы по классам, домашнее задание по математике 8 класса [[Математика|скачать]]</sub> | | ''<br>Мордкович А. Г., Алгебра. 8 кл.: Учеб. для общеобразоват. учреждений.— 3-е изд., доработ. — М.: Мнемозина, 2001. — 223 с: ил. ''<br><br><sub>Планирование уроков по математике [[Гипермаркет знаний - первый в мире!|онлайн]], задачи и ответы по классам, домашнее задание по математике 8 класса [[Математика|скачать]]</sub> |
Текущая версия на 06:09, 8 октября 2012
Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика:Сложение и вычитание алгебраических дробей с одинаковыми знаменателями
Сложение и вычитание алгебраических дробей с одинаковыми знаменателями
Алгебраические дроби с одинаковыми знаменателями складывают и вычитают по тому же правилу, что и обыкновенные дроби:
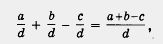
т. е. составляют соответствующую алгебраическую сумму числителей, а знаменатель оставляют без изменений.
Пример. Выполнить действия:
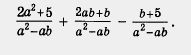
Решение. Применив правило сложения и вычитания алгебраических дробей, получим
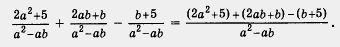
Теперь можно упростить числитель, выполнив обычным образом соответствующие операции над многочленами:
(2а2 + 5) +(2аb + b) - (b + 5) =
= 2а2 + 5 + 2аb + b - b - 5 = 2а2 + 2аb.
Таким образом, заданную алгебраическую сумму трех дробей нам удалось преобразовать в дробь —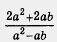 . .
А теперь вспомните то, что мы говорили в предыдущем параграфе: получив алгебраическую дробь, нужно посмотреть, нельзя ли ее сократить.
Имеем
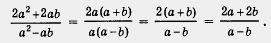
Приведем теперь решение рассмотренного примера без комментариев (как это вы будете делать у себя в тетрадях):
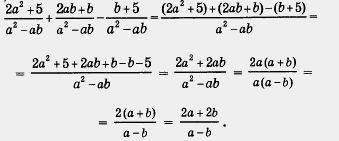
Как видите, в результате преобразований получилось более простое алгебраическое выражение, чем было задано в условии примера. Именно в упрощении и состоит цель преобразований, поэтому часто, вместо словосочетания «выполнить действия», используют словосочетание «упростить выражение».
Мордкович А. Г., Алгебра. 8 кл.: Учеб. для общеобразоват. учреждений.— 3-е изд., доработ. — М.: Мнемозина, 2001. — 223 с: ил.
Планирование уроков по математике онлайн, задачи и ответы по классам, домашнее задание по математике 8 класса скачать
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|