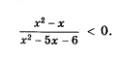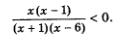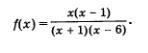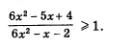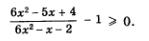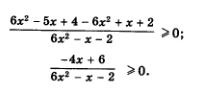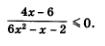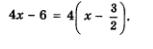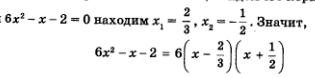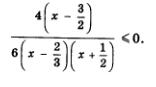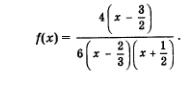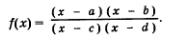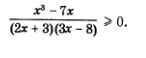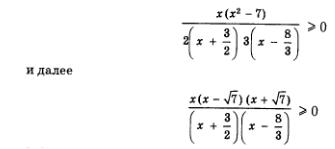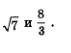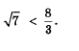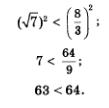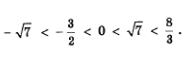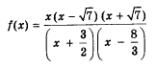|
|
|
| Строка 1: |
Строка 1: |
| | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 9 класс, урок, на Тему, Рациональные неравенства</metakeywords> |
| | + | |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 9 класс|Математика 9 класс]]>>Математика:Рациональные неравенства<metakeywords>Рациональные неравенства</metakeywords>''' <br> | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 9 класс|Математика 9 класс]]>>Математика:Рациональные неравенства<metakeywords>Рациональные неравенства</metakeywords>''' <br> |
| | | | |
Версия 05:07, 10 октября 2012
Гипермаркет знаний>>Математика>>Математика 9 класс>>Математика:Рациональные неравенства
Рациональные неравенства
Рациональное неравенство с одной переменной х — это неравенство вида 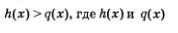 — рациональные выражения, т.е. алгебраические выражения, составленные из чисел и переменной х с помощью операций сложения, вычитания, умно-жения, деления и возведения в натуральную степень. Разумеется, переменная может быть обозначена любой другой буквой, но в математике чаще всего предпочтение отдается букве х. — рациональные выражения, т.е. алгебраические выражения, составленные из чисел и переменной х с помощью операций сложения, вычитания, умно-жения, деления и возведения в натуральную степень. Разумеется, переменная может быть обозначена любой другой буквой, но в математике чаще всего предпочтение отдается букве х.
При решении рациональных неравенств используются те три правила, которые были сформулированы выше в § 1. С помощью этих правил обычно преобразуют заданное рациональное неравенство к виду / (ж) > 0, где / (х) — алгебраическая дробь (или многочлен). Далее разлагают числитель и знаменатель дроби f (х) на множители вида х - а (если, конечно, это возможно) и применяют метод интервалов, который мы уже упоминали выше (см. в предыдущем параграфе пример 3).
Пример 1. Решить неравенство (х - 1) (х + 1) (х - 2) > 0.
Решение. Рассмотрим выражение f(х) = (х-1)(х + 1)(х-2).
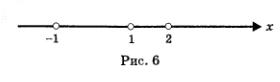
Оно обращается в 0 в точках 1,-1,2; отметим эти точки на числовой прямой. Числовая прямая разбивается указанными точками на четыре промежутка (рис. 6), на каждом из которых выражение f (x) сохраняет постоянный знак. Чтобы в этом убедиться, проведем четыре рассуждения (для каждого из указанных промежутков в отдельности).
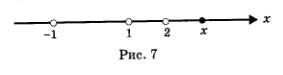
Возьмем любую точку х из промежутка (2, Эта точка расположена на числовой прямой правее точки -1, правее точки 1 и правее точки 2. Это значит, что х > -1, х >1, х > 2 (рис. 7). Но тогда x-1>0, х+1>0, х - 2 > 0, а значит, и f (х) > 0 (как произведение рациональное неравенство трех положительных чисел). Итак, на всем промежутке 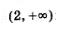 выполняется неравенство f (x) > 0. выполняется неравенство f (x) > 0.
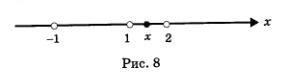
Возьмем любую точку х из интервала (1,2). Эта точка расположена на числовой прямой правее точки-1, правее точки 1, но левее точки 2. Значит, х > -1, х > 1, но х < 2 (рис. 8), а потому x + 1>0,x-1>0,x-2<0. Но тогда f(x) <0 (как произведение двух положительных и одного отрицательного числа). Итак, на промежутке (1,2) выполняется неравенство f (x) < 0.
Возьмем любую точку х из интервала (-1,1). Эта точка расположена на числовой прямой правее точки -1, левее точки 1 и левее точки 2. Значит, х >-1, но х< 1, х <2 (рис. 9), а потому х + 1 > 0, х -1 <0, х - 2 < 0. Но тогда f (x) > 0 (как произведение двух отрицательных и одного положительного числа). Итак, напромежутке (-1,1) выполняется неравенство f (x)> 0.
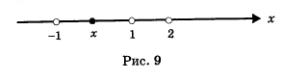
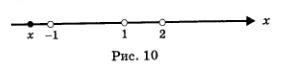
Возьмем, наконец, любую точку х из открытого луча (-оо, -1). Эта точка расположена на числовой прямой левее точки -1, левее точки 1 и левее точки 2. Это значит, что x<-1, х< 1, х<2 (рис. 10). Но тогда x - 1 < 0, x + 1 < 0, х - 2 < 0, а значит, и f (x) < 0 (как произведение трех отрицательных чисел). Итак, на всем промежутке (-оо, -1) выполняется неравенство f (x) < 0.
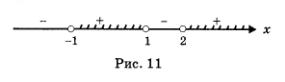
Подведем итоги. Знаки выражения f (x) в выделенных промежутках таковы, как показано на рис. 11. Нас интересуют те из них, на которых выполняется неравенство f (x) > 0. С помощью геометрической модели, представленной на рис. 11, устанавливаем, что неравенство f (x) > 0 выполняется на интервале (-1, 1) или на открытом луче 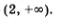
О т в е т: -1 < х < 1; х > 2.
Пример 2. Решить неравенство 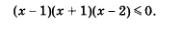
Решение. Как и в предыдущем примере, почерпнем необходимую информацию из рис. 11, но с двумя изменениями по сравнению с примером 1. Во-первых, поскольку нас интересует, при каких значениях х выполняется неравенство f (x) < 0, нам придется выбрать промежутки 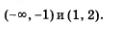 Во-вторых, нас устраивают и те точки, в которых выполняется равенство f (x) = 0. Это точки -1, 1, 2, отметим их на рисунке темными кружочками и включим в ответ. На рис. 12 представлена геометрическая модель ответа, от которой нетрудно перейти к аналитической записи. Во-вторых, нас устраивают и те точки, в которых выполняется равенство f (x) = 0. Это точки -1, 1, 2, отметим их на рисунке темными кружочками и включим в ответ. На рис. 12 представлена геометрическая модель ответа, от которой нетрудно перейти к аналитической записи.
Ответ: 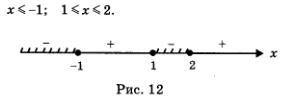
П р и м е р 3. Решить неравенство 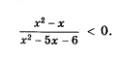
Решение. Разложим на множители числитель и знаменатель алгебраической дроби fх, содержащейся в левой части неравенства. В числителе имеем х2- х = х(х - 1).
Чтобы разложить на множители квадратный трехчлен х2 - bх ~ 6, содержащийся в знаменателе дроби, найдем его корни. Из уравнения х2 - 5х - 6 = 0 находим х1 = -1, х2 = 6. Значит, 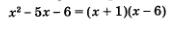 (мы воспользовались формулой разложения на множители квадратного трехчлена: ах2 + bх + с = а(х - х1 - х2)). (мы воспользовались формулой разложения на множители квадратного трехчлена: ах2 + bх + с = а(х - х1 - х2)).
Тем самым мы преобразовали заданное неравенство к виду
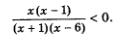
Рассмотрим выражение:
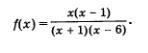
Числитель этой дроби обращается в 0 в точках 0 и 1, а знаменатель обращается в 0 в точках -1 и 6. Отметим эти точки на числовой прямой (рис. 13). Числовая прямая разбивается указанными точками на пять промежутков, причем на каждом промежутке выражение fх) сохраняет постоянный знак. Рассуждая так же, как в примере 1, приходим к выводу, что знаки выражения fх) в выделенных промежутках таковы, как показано на рис. 13. Нас интересует, где выполняется неравенство f (x) < 0. С помощью геометрической модели, представленной на рис. 13, устанавливаем, что f (х) < 0 на интервале (-1, 0) или на интервале (1, 6).
0твет: -1<x <0; 1<x<6.

Пример 4. Решить неравенство
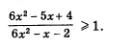
Решение. При решении рациональных неравенств, как правило, предпочитают оставлять в правой части неравенства только число 0. Поэтому преобразуем неравенство к виду
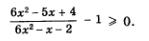
Далее:
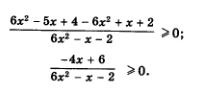
Как показывает опыт, если в правой части не(ра-венства содержится лишь число 0, удобнее проводить рассуждения, когда в левой его части и числитель и знаменатель имеют положительный старший коэффициент. А что у нас? У нас в знаменателе дроби в этом смысле все в порядке (старший коэффициент, т.е. коэффициент при х2, равен 6 — положительное число), но в числителе не все в порядке — старший коэффициент (коэффициент при х) равен -4 (отрицательное число). Умножив обе части неравенства на -1 и изменив при этом знак неравенства на противоположный, получим равносильное ему неравенство
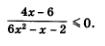
Разложим числитель и знаменатель алгебраической дроби 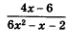 на множители. В числителе все просто: на множители. В числителе все просто: 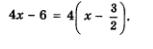
Чтобы разложить на множители содержащийся в знаменателе дроби квадратный трехчлен 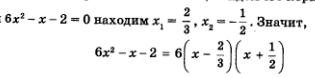
(мы снова воспользовались формулой разложения на множители квадратного трехчлена).
Тем самым заданное неравенство мы привели к виду
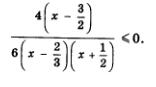
Рассмотрим выражение
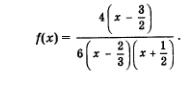
Числитель этой дроби обращается в 0 в точке 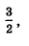 а знаменатель — в точках а знаменатель — в точках 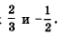 Отметим эти точки на числовой прямой (рис. 14), которая разбивается указанными точками на четыре промежутка, причем на каждом промежутке выражение f (х) сохраняет постоянный знак (эти знаки указаны на рис. 14). Нас интересуют те промежутки, на которых выполняется неравенство fх < 0; эти промежутки выделены штриховкой на рис. 15. По условию, нас интересуют и те точки х, в которых выполняется равенство f (х) = 0. Такая точка только одна — это точка Отметим эти точки на числовой прямой (рис. 14), которая разбивается указанными точками на четыре промежутка, причем на каждом промежутке выражение f (х) сохраняет постоянный знак (эти знаки указаны на рис. 14). Нас интересуют те промежутки, на которых выполняется неравенство fх < 0; эти промежутки выделены штриховкой на рис. 15. По условию, нас интересуют и те точки х, в которых выполняется равенство f (х) = 0. Такая точка только одна — это точка 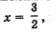 поскольку лишь при этом значении числитель дроби f (х) обращается в нуль. Точка поскольку лишь при этом значении числитель дроби f (х) обращается в нуль. Точка 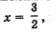 отмечена на рис. 15 темным кружочком. Таким образом, на рис. 15 представлена геометрическая модель решения заданного неравенства, от которой нетрудно перейти к аналитической записи. отмечена на рис. 15 темным кружочком. Таким образом, на рис. 15 представлена геометрическая модель решения заданного неравенства, от которой нетрудно перейти к аналитической записи.
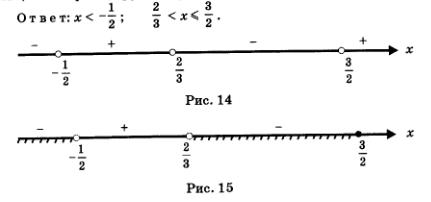
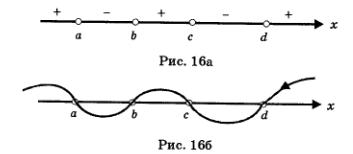
Во всех рассмотренных примерах мы преобразовывали заданное неравенство в равносильное ему неравенство вида f {х) > 0 или f (x) <0,где 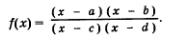
При этом количество множителей в числителе и знаменателе дроби может быть любым. Затем отмечали на числовой прямой точки а,Ь,с,д. и определяли знаки выражения f (х) на выделенных промежутках. Заметили, что на самом правом из выделенных промежутков выполняется неравенство f (х) > 0, а далее по промежуткам знаки выражения f (х) чередуются (см. рис. 16а). Это чередование удобно иллюстрировать с помощью волнообразной кривой, которая чертится справа налево и сверху вниз (рис. 166). На тех промежутках, где эта кривая (ее иногда называют кривой знаков) расположена выше оси х, выполняется неравенство f (х) > 0; где эта кривая расположена ниже оси х, выполняется неравенство f (х) < 0.
Пример 5. Решить неравенство
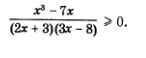
Решение. Имеем
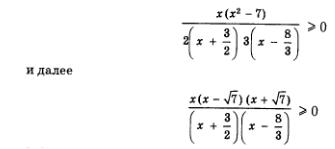
(обе части предыдущего неравенства умножили на положительное число 6).
Чтобы воспользоваться методом интервалов, отметим на числовой прямой точки 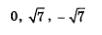 (в этих точках числитель дроби, содержащейся в левой части неравенства, обращается в нуль) и точки (в этих точках числитель дроби, содержащейся в левой части неравенства, обращается в нуль) и точки  (в этих точках знаменатель указанной дроби обращается в нуль). Обычно точки отмечают схематически, учитывая порядок их следования (какое — правее, какое — левее) и не особенно обращая внимания на соблюдение масштаба. Ясно, что (в этих точках знаменатель указанной дроби обращается в нуль). Обычно точки отмечают схематически, учитывая порядок их следования (какое — правее, какое — левее) и не особенно обращая внимания на соблюдение масштаба. Ясно, что 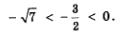 Сложнее обстоит дело с числами Сложнее обстоит дело с числами 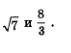 Первая прикидка показывает, что и то и другое число чуть больше, чем 2,6, откуда нельзя сделать вывод о том, какое из указанных чисел больше, а какое — меньше. Предположим (наугад), что Первая прикидка показывает, что и то и другое число чуть больше, чем 2,6, откуда нельзя сделать вывод о том, какое из указанных чисел больше, а какое — меньше. Предположим (наугад), что 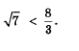 Тогда Тогда 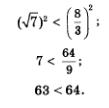
Получилось верное неравенство, значит, наша догадка подтвердилась: на самом деле 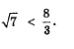
Итак,
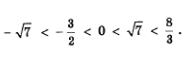
Отметим указанные 5 точек в указанном порядке на числовой прямой (рис. 17а). Расставим знаки выражения 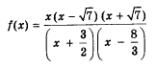
на полученных промежутках: на самом правом — знак +, а далее знаки чередуются (рис. 176). Начертим кривую знаков и выделим (штриховкой) те промежутки, на которых выполняется интересующее нас неравенство f (x) > 0 (рис. 17в). Учтем, наконец, что речь идет о нестрогом неравенстве f (x) > 0, значит, нас интересуют и те точки, в которых выражение f (x) обращается в нуль. Это — корни числителя дроби f (x), т.е. точки 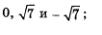 отметим их на рис. 17в темными кружочками (и, естественно, включим в ответ). Вот теперь рис. 17в дает полную геометрическую модель решений заданного неравенства. отметим их на рис. 17в темными кружочками (и, естественно, включим в ответ). Вот теперь рис. 17в дает полную геометрическую модель решений заданного неравенства.
А.Г. Мордкович Алгебра 9 класс
Материалы по математике онлайн, задачи и ответы по классам, планы конспектов уроков по математике скачать
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|