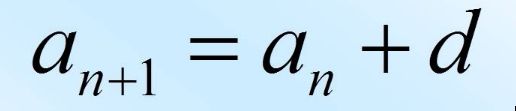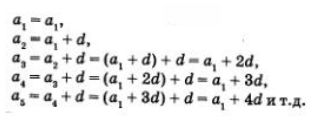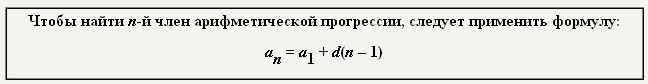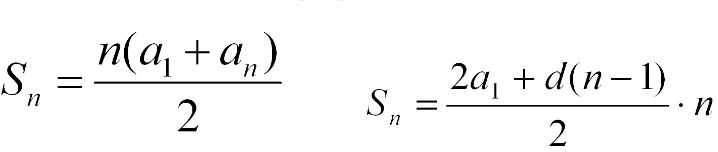KNOWLEDGE HYPERMARKET

Арифметическая прогрессия
Строка 3: Строка 3:
<br>  
<br>  
-
'''Арифметическая прогрессия'''<br>
+
<h2> Определение арифметической прогрессии</h2>
-
<u><br></u>'''1. Основные понятия.'''<br>
+
Арифметической прогрессией называют такую последовательность, в которой каждый член, начиная со второго, равняется предыдущему, к которому прибавляют одно и то же число.
-
'''Определение.''' Числовую последовательность, каждый член которой, начиная со второго, равен сумме предыдущего члена и одного и того же числа d, называют арифметической прогрессией, а число d — разностью [[Конспект уроку «Арифметична прогресія, її властивості. Формула n-го члена арифметичної прогресії»|арифметической прогрессии]].<br>
+
Число d, которое в переводе обозначает слово «разница», носит название разницы арифметической прогрессии.  
-
Таким образом, арифметическая прогрессия — это числовая последовательность (а<sub>n</sub>), заданная рекуррентно соотношениями  
+
Иными словами можно сказать, что арифметическая прогрессия — это числовая последовательность (аn), заданная рекуррентно соотношениями  
-
[[Image:Al9161.jpg|240px|Арифметическая прогрессия]]<br>(а и д, — заданные числа).<br>
+
<br>
 +
[[Image:9kl_ArProgressia01.jpg|500x500px|пифагор]]
 +
<br>
-
Можно ли, глядя на [[Числові послідовності. Властивості числових послідовностей. Презентація уроку|числовую последовательность]], определить, является ли она арифметической прогрессией? Можно. Если вы убедились в том, что разность между любым членом последовательности и предшествующим ему членом постоянна [[Image:Al9162.jpg|240px|Арифметическая прогрессия]]то перед вами — арифметическая прогрессия. Разумеется, при этом предполагается, что обнаруженная закономерность справедлива не только для явно выписанных членов последовательности, но и для всей последовательности в целом.<br>
+
При этом n = 2, 3, 4
-
'''Пример 1.''' <br>
+
Где, a и d являются заданными числами.
-
1, 3, 5, 7, 9,11,... .<br>Это арифметическая прогрессия, у которой а<sub>1</sub> = 1, d = 2.<br>
+
То есть, такая числовая последовательность, как a1, a2, а3, ..., аn ... считается арифметической прогрессией.  
-
'''Пример 2.'''<br>
+
Иначе говоря, числовая последовательность a1, a2, а3, ..., а n ... является арифметической прогрессией, если для любого натурального числа n выполняется условие an + 1 = an + d. Из этого равенства следует равенство an + 1 - an = d которая означает, что разница между любым следующим и предыдущим членами арифметической прогрессии р.
-
20,17, 14, 11, 8, 5, 2, -1, -4, ... .<br>Это арифметическая прогрессия, у которой а<sub>1</sub> = 20, d = -3.<br>
+
'''Например'''
-
'''Пример 3.'''<br>
+
Если взять последовательность чисел 4; 12; 20; 25; 36, то мы увидим, что каждое последующее число на восемь больше предыдущего. Такая последовательность получается за счет прибавления числа восемь к каждому следующему члену.  
-
8, 8, 8, 8, 8, 8,... .<br>Это арифметическая прогрессия, у которой а<sub>1</sub> = 8, d = 0.<br>
+
-
Очевидно, что арифметическая прогрессия является возрастающей последовательностью, если d &gt; 0 (см. пример 1), и убывающей, если d &lt; 0 (см. пример 2).<br>
+
Вот такая получается арифметическая прогрессия:
-
Для обозначения того, что последовательность (а<sub>n</sub>) является арифметической прогрессией, иногда бывает удобна следующая запись:
+
• 4+8=12<br>
 +
• 12+8=17<br>
 +
• 20+8=28<br>
 +
• 28+8=31<br>
-
[[Image:Al9163.jpg|180px|Арифметическая прогрессия]]<br>Значок + заменяет словосочетание «арифметическая прогрессия».<br>
+
Для обозначения арифметической последовательности (аn), удобной является такая запись, как:
-
Если в арифметической прогрессии отбросить все члены, следующие за каким-то конкретным членом последовательности, например за а<sub>n</sub>, то получится конечная арифметическая прогрессия
+
+ a1, a2, а3, ..., аn ...
-
[[Image:Al9164.jpg|160px|Арифметическая прогрессия]]<br>Иногда в конечной арифметической прогрессии удобно записывать не только несколько членов в начале, но и несколько членов в конце, например так:
+
Здесь значок «+» служит заменой такого словосочетания, как «арифметическая прогрессия».
-
[[Image:Al9165.jpg|180px|Арифметическая прогрессия]]<br>В дальнейших пунктах этого параграфа рассмотрим наиболее важные свойства арифметической прогрессии.<br>
+
'''Задание'''
-
<br>2. [[Презентація уроку «Арифметична прогресія, її властивості. Формула n-го члена арифметичної прогресії»|Формула n-го члена]] арифметической прогрессии.<br>
+
Перед вами предоставлена такая последовательность чисел:
-
Задание арифметической прогрессии, о котором идет речь в определении, является рекуррентным. Во многих случаях оно неудобно: чтобы вычислить, например, аш, надо предварительно найти предшествующие 99 членов последовательности. Эту вычислительную работу можно существенно упростить, если удастся найти формулу n-го члена, т.е. перейти к аналитическому заданию арифметической прогрессии.<br>
+
3, 6, 9, 12, 15, 18,……
-
Рассмотрим арифметическую прогрессию [[Image:Al9166.jpg|120px|Арифметическая прогрессия]] с разностью й. Имеем:  
+
Дайте ответ на такие вопросы:
-
[[Image:Al9167.jpg|320px|Арифметическая прогрессия]]<br> Нетрудно догадаться, что для любого номера n справедливо равенство
+
1. Можно ли назвать изображенный перечень чисел арифметической прогрессией?<br>
 +
2. Назовите ее первый член.<br>
 +
3. Чему равен ее десятый член?<br>
 +
4. Найдите разность этой прогрессии.<br>
 +
5. Какой будет сумма первых четырнадцати ее членов?<br>
 +
6. К какой последовательности относится эта арифметическая прогрессия? К возрастающей или убывающей?<br>
 +
7. Сделайте запись формулы ее n-го члена.<br>
-
[[Image:Al9168.jpg|240px|Aормула n-го члена арифметической прогрессии]]<br>Это — формула n-го члена арифметической прогрессии.<br>
+
<h2> Формула арифметической прогрессии</h2>
-
Важное -замечание. «Нетрудно догадаться», «можно сообразить» и т.д. — это стилистические обороты из области интуиции, догадки, озарения. Разумеется, математики ими пользуются, но в основном для открытия каких-то новых фактов, а не для их обоснования. Формулу (1) мы «прочувствовали», но не обосновали. Приведем (для интересующихся) доказательство.<br>
+
Такое нахождение арифметической прогрессии, в котором чтобы вычислить аn, необходимо еще найти и 99 предшествующих членов последовательности, является не совсем удобным. Естественно, что такую вычислительную работу буден лучше выполнить при помощи формулы n-го члена, то есть осуществить аналитическое задание арифметической прогрессии.  
-
Если [[Image:Al9169.jpg|180px|Равенство]] верное равенство, т.е. формула (1) для n = 1 верна.<br>
+
Припустим, что первый член арифметической прогрессии равен а1, а d - разница.  
-
Предположим, что формула (1) верна для [[Обозначение натуральных чисел|натурального числа]] n — к, т.е. предположим, что верно равенство [[Image:Al91610.jpg|120px|Равенство]]&nbsp; Докажем, что тогда формула (1) верна и для следующего натурального числа л = к+ 1, т.е. докажем, что [[Image:Al91611.jpg|120px|Равенство]]<br>В самом деле, по определению арифметической прогрессии, [[Image:Al91612.jpg|120px|Равенство]]&nbsp; Далее имеем [[Image:Al91613.jpg|320px|Равенство]]
+
Тогда:
-
А теперь смотрите: для d = 1 формула (1) верна (это мы проверили). Далее мы доказали, что если формула (1) верна для d = k, то она верна и для n = k + 1. Воспользуемся этим: формула (1) верна для n — 1, значит, она верна и для n = 2; так как она верна для n — 2, то она верна и для n = 3 и т.д. Значит, формула (1) верна для любого натурального числа n.<br>
+
<br>
 +
[[Image:9kl_ArProgressia02.jpg|500x500px|пифагор]]
 +
<br>
 +
 +
Мы видим, что в этих формулах коэффициент при числе d на один меньше порядкового номера члена прогрессии.  
-
Приведенный метод рассуждений носит название «метод математической индукции».<br>
+
<br>
 +
[[Image:9kl_ArProgressia03.jpg|500x500px|пифагор]]
 +
<br>
 +
<br>
 +
[[Image:9kl_ArProgressia04.jpg|500x500px|пифагор]]
 +
<br>  
-
Перепишем формулу n-го члена арифметической прогрессии [[Image:Al91614.jpg|120px|Формула]] в виде [[Image:Al91615.jpg|120px|Формула]] и введем обозначения: [[Image:Al91616.jpg|120px|Формула]] Получим у = dn + m, или, подробнее, [[Image:Al91617.jpg|120px|Формула]]<br>
+
<h2> Формула суммы членов конечной арифметической прогрессии</h2>
-
Значит, арифметическую прогрессию можно рассматривать как [[Розв'язування системи лінійних рівнянь з двома змінними способом додавання|линейную функцию]] (у = dх + m), заданную на множестве N натуральных чисел. Угловой коэффициент этой линейной функции равен й — разности арифметической прогрессии. На рис. 95 схематически изображен график арифметической прогрессии — изолированные точки на прямой (с абсциссами х = 1, х = 2, х = 3 и т.д.).
+
<br>
 +
[[Image:9kl_ArProgressia05.jpg|500x500px|пифагор]]
 +
<br>
-
[[Image:Al91618.jpg|240px|График]]<br>
+
<h2> Характеристическое свойство арифметической прогрессии</h2>
-
Вернемся к примерам 1, 2 и 3, рассмотренным выше. 1) 1, 3, 5, 7, 9, 11, ... . Это арифметическая прогрессия, у которой ах — 1, d = 2. Составим формулу n-го члена:
+
<br>
 +
[[Image:9kl_ArProgressia06.jpg|500x500px|пифагор]]
 +
<br>
-
[[Image:Al91619.jpg|160px|Арифметическая прогрессия]]<br>(заметим, что эту формулу нетрудно было угадать, глядя на заданную последовательность нечетных чисел 1, 3, 5, 7, ...).
+
'''Задание'''
-
2)&nbsp;&nbsp;&nbsp; 20, 17, 14, 11, 8, 5, 2, -1, -4, ... . Это арифметическая прогрессия, у которой а<sub>1</sub> = 20, d = -3. Составим формулу n-го члена:  
+
Решите несколько бытовых задач:
-
[[Image:Al91620.jpg|160px|Формула]]<br>3)&nbsp;&nbsp;&nbsp; 8,8, 8.....Это арифметическая прогрессия, у которой а<sub>1</sub> = 8, d = 0. Составим формулу n-го члена:
+
1. По рекомендации санаторного врача, отдыхающим было рекомендовано начинать принимать загар с пяти минут, увеличивая ежедневно время пребывание на солнце, еще на пять минут. Сколько дней будет длиться путевка в санатории, если время загара увеличится до 30 минут?<br>
-
[[Image:Al91621.jpg|160px|Формула]]<br>'''Пример 4.''' Дана арифметическая прогрессия
+
2. Спортсмен за час пробегает расстояние в 10 км. Каждый следующий час бега его расстояние уменьшается на 0,5 км, чем предыдущий. За сколько времени он пробежит 50 км?<br>
-
[[Image:Al91622.jpg|420px|Арифметическая прогрессия]]<br>'''Решение.''' Во всех случаях в основе решения лежит формула n-го члена арифметической прогрессии
+
3. В театре сидячие места расположены так, что в каждом следующем ряду количество кресел на четыре больше, чем в предыдущем, а всего в зале насчитывается 1050 мест. Назовите количество рядов в зале, если первый ряд насчитывает десять кресел?<br>
-
[[Image:Al91623.jpg|160px|Формула]]<br>а)&nbsp;&nbsp;&nbsp; Положив в формуле n-го члена арифметической прогрессии n = 22,получим<br>[[Image:Al91624.jpg|240px|Формула]]<br>б)&nbsp;&nbsp;&nbsp; Имеем<br>[[Image:Al91625.jpg|320px|Формула]]
+
<h2> Историческая справка</h2>
-
Решая составленное линейное уравнение, находим:
+
А известно ли вам, что создание формулы 1-х n – членов арифметической прогрессии тесно переплетается с именем такого ученого, как Карл Фридрих Гаусс. Будучи еще совсем ребенком, он проявлял себя истинным вундеркиндом, и кроме того, что умел читать и писать, умудрялся исправлять ошибки отца в подсчетах.
-
[[Image:Al91626.jpg|120px|Уравнение]]<br>в)&nbsp;&nbsp;&nbsp; Имеем
+
Если верить легенде, то во время учебы, когда учитель предложил детям сосчитать сумму чисел от одного до ста, то восьмилетний Карл Гаусс очень быстро нашел искомую величину, так как смог заметить, что попарные суммы с противоположных сторон имеют одинаковый результат. Немного позднее он вывел формулу арифметической прогрессии.
-
[[Image:Al91627.jpg|320px|Решение]]<br> Из этого [[Системы уравнений. Основные понятия|уравнения]] находим а<sub>1</sub> = 159.<br>
+
А вот «прогрессия», как термин появился в шестом веке благодаря римлянину Боэцию и воспринимался, как бесконечная числовая последовательность. И уже древние греки из теории непрерывных пропорций выделили такие названия, как «арифметическая» и «геометрическая» прогрессия.
-
г) Имеем
+
Задание: А вы сможете быстро подсчитать сумму от 1 до 100? Может среди нас тоже есть Гауссы-вундеркинды?
-
[[Image:Al91628.jpg|320px|Решение]]<br>
+
<h2> Интересные факты</h2>
-
Из этого уравнения находим: 14d = -42, d = -3.<br>
+
В 1796 году Карл Фридрих Гаусс решил окончательно посвятить себя математике, потому что обнаружил метод, который позволил построить правильный семнадцатиугольник только с помощью линейки и циркуля! Над этой задачей бились все  известные математики-геометры еще со времен великого Эвклида! А ведь изначально Гаусс собирался посвятить себя классической литературе, из-за необыкновенных склонностей к языкам.
-
Ответ: а) а<sub>22</sub> = 89; б) п = 41; в) а<sub>1</sub> = 159; г) d = -3.<br>
+
Некоторые факты, о математических прогрессиях были известны еще древним китайским и индийским мудрецам. Так, например, есть древняя индийская легенда, которая рассказывает об изобретении шахмат, а которой проходят моменты, связанные со знаниями арифметической прогрессии.  
-
'''Пример 5.''' <br>
+
Легенда рассказывает, как индийский шах Шерам пообещал награду тому, кто придумает интересную игр, которая вызовет длительный интерес у индийского владыки. Но мудрец Сета, который придумал шахматы, попросил за ее изобретение такое количество зерен, которое будет увеличиваться в зависимости от клеток на шахматной доске. И если на первую клеточку нужно положить только одно зернышко, то на следующую в два раза больше. И так каждый раз количество зерен на каждой следующей клетке снова удваивается по сравнению с предыдущей и т.д. вплоть до шестьдесят четвертой клетки. 
 +
Это значит, что количество зерен равняется сумме шестидесяти четырех членной геометрической прогрессии. В итоге должно было получиться такое число зерен, которое нужно было бы собирать со всей планеты. Поэтому шах просьбу ученого выполнить никак не мог. 
-
При делении девятого члена арифметической прогрессии на второй ее член в частном получается 7; при делении десятого члена прогрессии на ее пятый член в частном получается 2 и в остатке 5. Найти двадцатый член этой прогрессии.<br>
+
А вот с помощью вычислений английский математик Абрахам де Муавр смог предсказать дату своей кончины. Наблюдая за продолжительностью своего сна, он заметил, что она с каждым днем увеличивается на пятнадцать минут в день и, рассчитав арифметическую прогрессию, он узнал дату своей смерти и в этот же день и умер.  
-
'''Решение. '''<br>
+
'''Задание:''' А известно ли вам, с какой легендой связано создание геометрической прогрессии?
-
Первый этап. <br>
+
-
Составление [[Что такое математическая модель|математической модели]].<br>
+
<h2> Домашнее задание</h2>
-
Условия задачи можно кратко записать так:
+
Посмотрите внимательно на схему, изображенную внизу, и укажите с помощью стрелочек, какому определению соответствует формула, изображенная в овале?
-
 
+
-
[[Image:Al91629.jpg|240px|Задача]]<br>Воспользовавшись (несколько раз) формулой n-го члена арифметической прогрессии, получим:
+
-
 
+
-
[[Image:Al91630.jpg|120px|Решение]]<br>Тогда второе условие задачи (а<sub>9</sub> = 7а<sub>2</sub>) можно записать в виде
+
-
 
+
-
[[Image:Al91631.jpg|320px|Задача]]<br>Третье условие задачи (а<sub>10</sub>= 2а<sub>5</sub> + 5) можно записать в виде
+
-
 
+
-
[[Image:Al91632.jpg|320px|Задача]]
+
-
 
+
-
В итоге получаем очень простую систему двух линейных уравнений с двумя переменными а<sub>1</sub> и d:
+
-
 
+
-
[[Image:Al91633.jpg|120px|Система уравнений]]<br>которая в сочетании с записанным выше условием 1) и представляет собой математическую модель задачи.<br>
+
-
 
+
-
Второй этап. <br>
+
-
 
+
-
Работа с составленной моделью.<br>
+
-
 
+
-
Решая систему, находим a<sub>1</sub> = 1, d = 6.<br>
+
-
 
+
-
Теперь мы можем записать арифметическую прогрессию 1,7, 13,19, 25,31,....<br>
+
-
 
+
-
<br>Третий этап.<br>
+
-
 
+
-
Ответ на вопрос задачи.<br>
+
-
 
+
-
Требуется вычислить а<sub>20</sub>. Имеем [[Image:Al91634.jpg|240px|Решение]]<br>Ответ: а<sub>20</sub> = 115.<br>
+
-
 
+
-
<br>'''Замечание.''' <br>
+
-
 
+
-
В рассмотренном примере речь шла о конкретной математической модели — арифметической прогрессии. Первый этап решения мы назвали, как обычно, «составление математической модели». Получается, что мы составили математическую модель для математической модели. Как это понимать? Дело в том, что при решении задач очень часто приходится заменять одну математическую модель другой, более простой. Так обстоит дело и в рассмотренной задаче: математическую модель, оформленную в виде условий 1), 2) и 3), нам удалось заменить более привычной моделью — [[Системи рівнянь з двома змінними. Графічний спосіб розв’язання систем рівнянь з двома змінними|системой уравнений]].<br>
+
<br>
<br>
-
 
+
[[Image:9kl_ArProgressia07.jpg|500x500px|пифагор]]
-
'''3. Формула суммы членов конечной арифметической прогрессии.'''<br>
+
<br>
-
 
+
-
Пусть дана конечная арифметическая прогрессия
+
-
 
+
-
[[Image:Al01635.jpg|240px|Арифметическая прогрессия ]]<br>Обозначим через Sn сумму ее членов, т.е.<br>
+
-
 
+
-
[[Image:Al91636.jpg|240px|Арифметическая прогрессия ]]<br>
+
-
 
+
-
Выведем формулу для нахождения этой суммы.<br>
+
-
 
+
-
Для начала заметим, что [[Image:Al91637.jpg|120px|Арифметическая прогрессия ]]<br>В самом деле, по определению арифметической прогрессии,
+
-
 
+
-
[[Image:Al91638.jpg|320px|Арифметическая прогрессия ]]<br>Аналогично можно установить, что [[Image:Al91639.jpg|180px|Арифметическая прогрессия ]] и вообще что сумма члена, находящегося на к-м месте от начала конечной арифметической прогрессии, и члена, находящегося на к-м месте от ее конца, равна сумме первого и последнего членов прогрессии.<br>
+
-
 
+
-
Рассмотрим конкретный пример отыскания Sn. Дана конечная арифметическая прогрессия 1, 2, 3, ..., 98, 99, 100. <br>
+
-
 
+
-
Сумму ее членов вычислим следующим образом:
+
-
 
+
-
[[Image:Al91640.jpg|420px|Арифметическая прогрессия ]]<br>
+
-
 
+
-
<br>'''Замечание.''' <br>
+
-
 
+
-
Рассказывают, что немецкий математик XIX века Карл Фридрих Гаусс додумался до приведенного выше решения примера в возрасте 5 лет. Применим аналогичную идею для произвольной арифметической прогрессии. Имеем:
+
-
 
+
-
[[Image:Al91641.jpg|320px|Арифметическая прогрессия ]]<br>Сложив эти два равенства, получим
+
-
 
+
-
[[Image:Al91642.jpg|320px|Арифметическая прогрессия ]]<br>В правой части равенства n пар слагаемых, каждая пара, как мы установили выше, равна а<sub>1</sub> + а<sub>n</sub>. Значит, получаем
+
-
 
+
-
[[Image:Al91643.jpg|180px|Формула]]<br>Это — формула суммы n членов арифметической прогрессии.<br>
+
-
 
+
-
'''Пример 6.''' <br>
+
-
 
+
-
Дана конечная арифметическая прогрессия
+
-
 
+
-
[[Image:Al91644.jpg|420px|Арифметическая прогрессия ]]<br>'''Решение. '''<br>
+
-
 
+
-
а) Имеем
+
-
 
+
-
[[Image:Al91645.jpg|320px|Арифметическая прогрессия ]]<br>б) Сначала найдем
+
-
 
+
-
[[Image:Al91646.jpg|240px|Арифметическая прогрессия ]]
+
-
 
+
-
В итоге получаем, что а<sub>8</sub> = 28.<br>
+
-
 
+
-
А теперь применим к а<sub>8</sub> формулу п-го члена арифметической прогрессии а<sub>8</sub> = а1 + 16,, т.е. 28 = 7 + d, откуда находим d = 3.
+
-
 
+
-
'''Ответ: '''а)S<sub>22</sub>= 1034; б) d = 3.
+
-
 
+
-
<br>'''Пример 7.'''
+
-
 
+
-
Найти сумму всех четных [[Усне додавання і віднімання трицифрових чисел. Письмове ділення трицифрових чисел на одноцифрове|трехзначных чисел]]. Решение. Речь идет о сумме членов конечной арифметической прогрессии 100,102,104,..., 998. У этой прогрессии а<sub>1</sub> = 100, а<sub>п</sub> = 998, d = 2. Нужно вычислить 8<sub>п</sub>, но для этого сначала надо узнать, чему равно п, т.е. сколько членов содержится в указанной конечной арифметической прогрессии. Имеем последовательно:
+
-
 
+
-
[[Image:Al91647.jpg|180px|Арифметическая прогрессия ]]<br>Итак, а<sub>1</sub> = 100, n = 450, а<sub>п</sub> = 998. Наша задача — вычислить&nbsp; [[Image:Al91648.jpg|Pflfybt]]<br>Имеем<br>[[Image:Al91649.jpg|320px|Решение]]<br>'''Ответ:''' 247 050.
+
-
 
+
-
Иногда оказывается полезной несколько видоизмененная формула суммы n членов арифметической прогрессии. Если в формуле для Sn учесть, что аn = а<sub>1</sub> + d(n - 1), то получим
+
-
 
+
-
[[Image:Al91650.jpg|180px|Формула]]
+
-
 
+
-
'''Пример 8.'''
+
-
 
+
-
Турист, двигаясь по сильно пересеченной местности, за первый час пути прошел 800 м, а за каждый следующий час проходил на 25 м меньше, чем за предыдущий. Сколько времени он потратил на весь путь, равный 5700 м?
+
-
 
+
-
'''Решение. '''
+
-
 
+
-
Первый этап.
+
-
Составление математической модели.
+
-
 
+
-
За первый час турист прошел 800 м, за второй — 775 м, за третий — 750 м и т.д. Математической моделью является конечная арифметическая прогрессия&nbsp;у которой а<sub>1</sub> = 800, d = -25, Sn = 5700. Надо найти n (в часах — время движения туриста).
+
-
 
+
-
Второй этап.
+
-
 
+
-
Работа с составленной моделью. Воспользуемся второй формулой для Sn
+
-
 
+
-
[[Image:Al91652.jpg|320px|Задание]]
+
-
 
+
-
<br>Третий этап.
+
-
 
+
-
Ответ на вопрос задачи.
+
-
 
+
-
Спрашивается, сколько времени был в пути турист. По смыслу задачи из двух найденных значений n выбираем первое: n = 8.
+
-
 
+
-
'''Ответ:''' турист был в пути 8 часов.
+
-
 
+
-
 
+
-
 
+
-
'''4. Характеристическое свойство арифметической прогрессии.'''
+
-
 
+
-
Пусть дана арифметическая прогрессия а<sub>1</sub> , а<sub>2</sub>, а<sub>3</sub>,..., а<sub>п</sub>,.... Рассмотрим три ее члена, следующие друг за другом: а<sub>п1</sub>, а<sub>п</sub>, а<sub>n+1</sub>. Известно, что
+
-
 
+
-
[[Image:Al91653.jpg|120px|Задание]]<br>Сложив эти равенства, получим
+
-
 
+
-
[[Image:Al91654.jpg|180px|Формула]]''<br>''Это значит, что каждый член арифметической прогрессии (кроме первого и последнего)равен [[Среднее арифметическое|среднему арифметическому]] предшествующего и последующего членов.
+
-
 
+
-
Верно и обратное: если последовательность (а<sub>n</sub>) такова, что для любого n &gt; 1 выполняется равенство
+
-
 
+
-
[[Image:Al91655.jpg|160px|Арифметическая прогрессия]]<br>то (а<sub>n</sub>) — арифметическая прогрессия.
+
-
 
+
-
В самом деле, последнее равенство можно переписать в виде[[Image:Al91656.jpg|160px|Равенство]]<br>Это значит, в частности, что [[Image:Al91657.jpg|320px|Равенство]]. Иными словами, разность между любым членом последовательности и предшествующим ему всегда одна и та же, а это и означает, что задана арифметическая прогрессия.
+
-
 
+
-
'''Тем самым мы доказали следующую теорему.'''
+
-
 
+
-
Числовая последовательность является арифметической прогрессией тогда и только тогда, когда каждый ее член, кроме первого (и последнего в случае конечной последовательности), равен среднему арифметическому предшествующего и последующего членов (характеристическое свойство арифметической прогрессии).
+
-
 
+
-
'''Пример 9.'''
+
-
 
+
-
При каком значении х числа Зх + 2, dх - 4 и dх + 12 образуют конечную арифметическую прогрессию?
+
-
 
+
-
'''Решение. '''
+
-
 
+
-
Согласно характеристическому свойству, заданные выражения должны удовлетворять соотношению
+
-
 
+
-
[[Image:Al91658.jpg|240px|Решение]]<br>Решая это уравнение, находим:
+
-
 
+
-
[[Image:Al91659.jpg|140px|Решение]]<br>При этом значении х заданные выражения Зх + 2, 5х - 4, 11х + 12 принимают соответственно значения -14,5, -31,5, -48,5. Это арифметическая прогрессия, ее разность равна -17.
+
-
 
+
-
'''Ответ:''' х = -5,5.
+
-
 
+
-
 
+
-
 
+
-
''А.Г. Мордкович [http://xvatit.com/vuzi/ Алгебра] 9 класс''
+
-
 
+
-
<br>
+
-
 
+
-
<sub>Материалы по математике [[Гипермаркет знаний - первый в мире!|онлайн]], задачи и ответы по классам, планы конспектов уроков по математике [[Математика|скачать]]</sub>
+
-
 
+
-
'''<u>Содержание урока</u>'''
+
-
'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока                      '''
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас 
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии
+
-
+
-
'''<u>Практика</u>'''
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников
+
-
+
-
'''<u>Иллюстрации</u>'''
+
-
'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа '''
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты
+
-
+
-
'''<u>Дополнения</u>'''
+
-
'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты'''
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов                         
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие
+
-
+
-
<u>Совершенствование учебников и уроков
+
-
</u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике'''
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми
+
-
+
-
'''<u>Только для учителей</u>'''
+
-
'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки '''
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год 
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации 
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы
+
-
[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения
+
-
+
-
+
-
'''<u>Интегрированные уроки</u>'''<u>
+
-
</u>
+
-
 
+
-
<br>
+
-
 
+
-
Если у вас есть исправления или предложения к данному уроку, [http://xvatit.com/index.php?do=feedback напишите нам].
+
-
 
+
-
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - [http://xvatit.com/forum/ Образовательный форум].
+

Версия 08:52, 20 мая 2015

Гипермаркет знаний>>Математика>>Математика 9 класс>>Математика: Арифметическая прогрессия


Содержание

Определение арифметической прогрессии

Арифметической прогрессией называют такую последовательность, в которой каждый член, начиная со второго, равняется предыдущему, к которому прибавляют одно и то же число.

Число d, которое в переводе обозначает слово «разница», носит название разницы арифметической прогрессии.

Иными словами можно сказать, что арифметическая прогрессия — это числовая последовательность (аn), заданная рекуррентно соотношениями


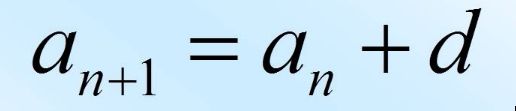
пифагор

При этом n = 2, 3, 4

Где, a и d являются заданными числами.

То есть, такая числовая последовательность, как a1, a2, а3, ..., аn ... считается арифметической прогрессией.

Иначе говоря, числовая последовательность a1, a2, а3, ..., а n ... является арифметической прогрессией, если для любого натурального числа n выполняется условие an + 1 = an + d. Из этого равенства следует равенство an + 1 - an = d которая означает, что разница между любым следующим и предыдущим членами арифметической прогрессии р.

Например

Если взять последовательность чисел 4; 12; 20; 25; 36, то мы увидим, что каждое последующее число на восемь больше предыдущего. Такая последовательность получается за счет прибавления числа восемь к каждому следующему члену.

Вот такая получается арифметическая прогрессия:

• 4+8=12
• 12+8=17
• 20+8=28
• 28+8=31

Для обозначения арифметической последовательности (аn), удобной является такая запись, как:

+ a1, a2, а3, ..., аn ...

Здесь значок «+» служит заменой такого словосочетания, как «арифметическая прогрессия».

Задание

Перед вами предоставлена такая последовательность чисел:

3, 6, 9, 12, 15, 18,……

Дайте ответ на такие вопросы:

1. Можно ли назвать изображенный перечень чисел арифметической прогрессией?
2. Назовите ее первый член.
3. Чему равен ее десятый член?
4. Найдите разность этой прогрессии.
5. Какой будет сумма первых четырнадцати ее членов?
6. К какой последовательности относится эта арифметическая прогрессия? К возрастающей или убывающей?
7. Сделайте запись формулы ее n-го члена.

Формула арифметической прогрессии

Такое нахождение арифметической прогрессии, в котором чтобы вычислить аn, необходимо еще найти и 99 предшествующих членов последовательности, является не совсем удобным. Естественно, что такую вычислительную работу буден лучше выполнить при помощи формулы n-го члена, то есть осуществить аналитическое задание арифметической прогрессии.

Припустим, что первый член арифметической прогрессии равен а1, а d - разница.

Тогда:


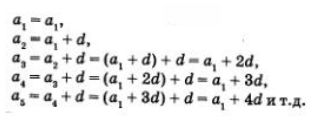
пифагор

Мы видим, что в этих формулах коэффициент при числе d на один меньше порядкового номера члена прогрессии.


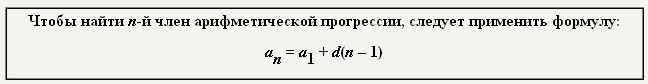
пифагор

пифагор

Формула суммы членов конечной арифметической прогрессии


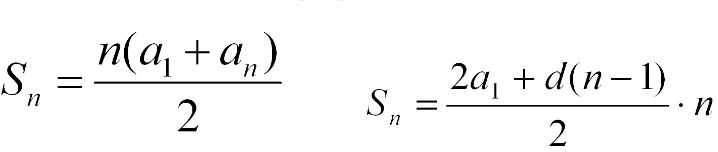
пифагор

Характеристическое свойство арифметической прогрессии


пифагор

Задание

Решите несколько бытовых задач:

1. По рекомендации санаторного врача, отдыхающим было рекомендовано начинать принимать загар с пяти минут, увеличивая ежедневно время пребывание на солнце, еще на пять минут. Сколько дней будет длиться путевка в санатории, если время загара увеличится до 30 минут?

2. Спортсмен за час пробегает расстояние в 10 км. Каждый следующий час бега его расстояние уменьшается на 0,5 км, чем предыдущий. За сколько времени он пробежит 50 км?

3. В театре сидячие места расположены так, что в каждом следующем ряду количество кресел на четыре больше, чем в предыдущем, а всего в зале насчитывается 1050 мест. Назовите количество рядов в зале, если первый ряд насчитывает десять кресел?

Историческая справка

А известно ли вам, что создание формулы 1-х n – членов арифметической прогрессии тесно переплетается с именем такого ученого, как Карл Фридрих Гаусс. Будучи еще совсем ребенком, он проявлял себя истинным вундеркиндом, и кроме того, что умел читать и писать, умудрялся исправлять ошибки отца в подсчетах.

Если верить легенде, то во время учебы, когда учитель предложил детям сосчитать сумму чисел от одного до ста, то восьмилетний Карл Гаусс очень быстро нашел искомую величину, так как смог заметить, что попарные суммы с противоположных сторон имеют одинаковый результат. Немного позднее он вывел формулу арифметической прогрессии.

А вот «прогрессия», как термин появился в шестом веке благодаря римлянину Боэцию и воспринимался, как бесконечная числовая последовательность. И уже древние греки из теории непрерывных пропорций выделили такие названия, как «арифметическая» и «геометрическая» прогрессия.

Задание: А вы сможете быстро подсчитать сумму от 1 до 100? Может среди нас тоже есть Гауссы-вундеркинды?

Интересные факты

В 1796 году Карл Фридрих Гаусс решил окончательно посвятить себя математике, потому что обнаружил метод, который позволил построить правильный семнадцатиугольник только с помощью линейки и циркуля! Над этой задачей бились все известные математики-геометры еще со времен великого Эвклида! А ведь изначально Гаусс собирался посвятить себя классической литературе, из-за необыкновенных склонностей к языкам.

Некоторые факты, о математических прогрессиях были известны еще древним китайским и индийским мудрецам. Так, например, есть древняя индийская легенда, которая рассказывает об изобретении шахмат, а которой проходят моменты, связанные со знаниями арифметической прогрессии.

Легенда рассказывает, как индийский шах Шерам пообещал награду тому, кто придумает интересную игр, которая вызовет длительный интерес у индийского владыки. Но мудрец Сета, который придумал шахматы, попросил за ее изобретение такое количество зерен, которое будет увеличиваться в зависимости от клеток на шахматной доске. И если на первую клеточку нужно положить только одно зернышко, то на следующую в два раза больше. И так каждый раз количество зерен на каждой следующей клетке снова удваивается по сравнению с предыдущей и т.д. вплоть до шестьдесят четвертой клетки. Это значит, что количество зерен равняется сумме шестидесяти четырех членной геометрической прогрессии. В итоге должно было получиться такое число зерен, которое нужно было бы собирать со всей планеты. Поэтому шах просьбу ученого выполнить никак не мог.

А вот с помощью вычислений английский математик Абрахам де Муавр смог предсказать дату своей кончины. Наблюдая за продолжительностью своего сна, он заметил, что она с каждым днем увеличивается на пятнадцать минут в день и, рассчитав арифметическую прогрессию, он узнал дату своей смерти и в этот же день и умер.

Задание: А известно ли вам, с какой легендой связано создание геометрической прогрессии?

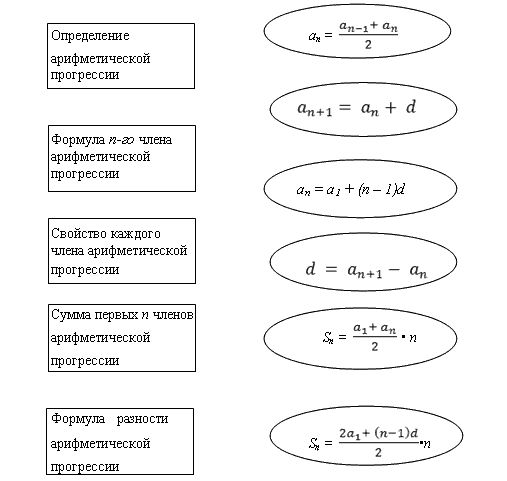
Домашнее задание

Посмотрите внимательно на схему, изображенную внизу, и укажите с помощью стрелочек, какому определению соответствует формула, изображенная в овале?


пифагор

Источник — «http://edufuture.biz/index.php?title=%D0%90%D1%80%D0%B8%D1%84%D0%BC%D0%B5%D1%82%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B0%D1%8F_%D0%BF%D1%80%D0%BE%D0%B3%D1%80%D0%B5%D1%81%D1%81%D0%B8%D1%8F»

Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки

©  Автор системы образования 7W и Гипермаркета Знаний - Владимир Спиваковский

При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов - гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.

Разработка - Гипермаркет знаний 2008-

Ждем Ваши замечания и предложения на email:
По вопросам рекламы и спонсорства пишите на email: