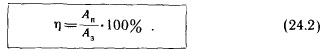|
|
|
| Строка 1: |
Строка 1: |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Физика и астрономия|Физика и астрономия]]>>[[Физика 7 класс|Физика 7 класс]]>>Физика: Коэффициент полезного действия'''<metakeywords>Физика, класс, урок, на тему, 7 класс, Коэффициент полезного действия</metakeywords> | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Физика и астрономия|Физика и астрономия]]>>[[Физика 7 класс|Физика 7 класс]]>>Физика: Коэффициент полезного действия'''<metakeywords>Физика, класс, урок, на тему, 7 класс, Коэффициент полезного действия</metakeywords> |
| | | | |
| - | <br>Используя тот или иной механизм, мы совершаем работу, всегда превышающую ту, которая необходима для достижения поставленной цели. В соответствии с этим различают полную или''затраченную работу'' А<sub>з</sub> и ''полезную работу'' А<sub>п</sub> . Если, например, наша цель-поднять груз массой ш на высоту Н, то полезная работа - это та, которая обусловлена лишь преодолением силы тяжести, действующей на груз. При равномерном подъеме груза, когда прикладываемая нами сила равна силе тяжести груза, эта работа может быть найдена следующим образом:<br>[[Файл:formula_24_1.jpg]] | + | <br>Используя тот или иной механизм, мы совершаем работу, всегда превышающую ту, которая необходима для достижения поставленной цели. В соответствии с этим различают полную или''затраченную работу'' А<sub>з</sub> и ''полезную работу'' А<sub>п</sub> . Если, например, наша цель-поднять груз массой ш на высоту Н, то полезная работа - это та, которая обусловлена лишь преодолением силы тяжести, действующей на груз. При равномерном подъеме груза, когда прикладываемая нами сила равна силе тяжести груза, эта работа может быть найдена следующим образом:<br>[[Image:Formula 24 1.jpg]] |
| | | | |
| - | Если же мы применяем для подъема груза блок или какой- либо другой механизм, то, кроме силы тяжести груза, нам приходится преодолевать еще и силу тяжести частей механизма, а также действующую в механизме силу трения. Например, используя подвижный блок, мы вынуждены будем совершать дополнительную работу по подъему самого блока с тросом и по преодолению силы трения в оси блока. Кроме того, выигрывая в силе, мы всегда проигрываем в пути (об этом подробнее будет рассказано ниже), что также влияет на работу. Все это приводит к тому, что затраченная нами работа оказывается больше полезной:<br> А<sub>з</sub> > А<sub>п</sub> . | + | Если же мы применяем для подъема груза блок или какой- либо другой механизм, то, кроме силы тяжести груза, нам приходится преодолевать еще и силу тяжести частей механизма, а также действующую в механизме силу трения. Например, используя подвижный блок, мы вынуждены будем совершать дополнительную работу по подъему самого блока с тросом и по преодолению силы трения в оси блока. Кроме того, выигрывая в силе, мы всегда проигрываем в пути (об этом подробнее будет рассказано ниже), что также влияет на работу. Все это приводит к тому, что затраченная нами работа оказывается больше полезной:<br> А<sub>з</sub> > А<sub>п</sub> . |
| | | | |
| - | ''Полезная работа всегда составляет лишь некоторую часть полной работы, которую совершает человек, используя механизм''. | + | ''Полезная работа всегда составляет лишь некоторую часть полной работы, которую совершает человек, используя механизм''. |
| | | | |
| - | Физическая величина, показывающая, какую долю составляет полезная работа от всей затраченной работы, называется '''коэффициентом полезного действия механизма.''' | + | Физическая величина, показывающая, какую долю составляет полезная работа от всей затраченной работы, называется '''коэффициентом полезного действия механизма.''' |
| | | | |
| - | Сокращенное обозначение коэффициента полезного действия - КПД. | + | Сокращенное обозначение коэффициента полезного действия - КПД. |
| | | | |
| - | ''Чтобы найти КПД механизма, надо полезную работу разделить на ту, которая была затрачена при использовании данного механизма.'' | + | ''Чтобы найти КПД механизма, надо полезную работу разделить на ту, которая была затрачена при использовании данного механизма.'' |
| | | | |
| - | Коэффициент полезного действия часто выражают в процентах и обозначают греческой буквой т) (читается "эта"):<br>[[Файл:formula_24_2.jpg]]<br>Поскольку числитель Ап в этой формуле всегда меньше знаменателя Аз, то КПД всегда оказывается меньше 1 (или 100%). | + | Коэффициент полезного действия часто выражают в процентах и обозначают греческой буквой и (читается "эта"):<br>[[Image:Formula 24 2.jpg]]<br>Поскольку числитель Ап в этой формуле всегда меньше знаменателя Аз, то КПД всегда оказывается меньше 1 (или 100%). |
| | | | |
| - | Конструируя механизмы, стремятся увеличить их КПД. Для этого уменьшают трение в осях механизмов и их массу. В тех случаях, когда трение ничтожно мало и используемые механизмы имеют массу, пренебрежимо малую по сравнению с массой поднимаемого груза, коэффициент полезного действия оказывается лишь немного меньше 1. В этом случае затраченную работу можно считать примерно равной полезной работе:<br>[[Файл:formula_24_3.jpg]]<br>Следует помнить, что ''выигрыша в работе с помощью простого механизма получить нельзя''. | + | Конструируя механизмы, стремятся увеличить их КПД. Для этого уменьшают трение в осях механизмов и их массу. В тех случаях, когда трение ничтожно мало и используемые механизмы имеют массу, пренебрежимо малую по сравнению с массой поднимаемого груза, коэффициент полезного действия оказывается лишь немного меньше 1. В этом случае затраченную работу можно считать примерно равной полезной работе:<br>[[Image:Formula 24 3.jpg]]<br>Следует помнить, что ''выигрыша в работе с помощью простого механизма получить нельзя''. |
| | | | |
| - | Поскольку каждую из работ в равенстве (24.3) можно выразить в виде произведения соответствующей силы на пройденный путь, то это равенство можно переписать так:<br>[[Файл:formula_24_4.jpg]]<br>Отсюда следует, что, | + | Поскольку каждую из работ в равенстве (24.3) можно выразить в виде произведения соответствующей силы на пройденный путь, то это равенство можно переписать так:<br>[[Image:Formula 24 4.jpg]]<br>Отсюда следует, что, |
| | | | |
| - | ''выигрывая с помощью механизма в силе, мы во столько же раз проигрываем в пути, и наоборот.''<br> | + | ''выигрывая с помощью механизма в силе, мы во столько же раз проигрываем в пути, и наоборот.''<br> |
| | | | |
| - | Этот закон называют '''"золотым правилом" механики.''' Его автором является древнегреческий ученый Герон Александрийский, живший в I в. н. э.<br>"Золотое правило" механики является приближенным законом, так как в нем не учитывается работа по преодолению трения и силы тяжести частей используемых приспособлений. Тем не менее оно бывает очень полезным при анализе работы любого простого механизма.<br> | + | Этот закон называют '''"золотым правилом" механики.''' Его автором является древнегреческий ученый Герон Александрийский, живший в I в. н. э.<br>"Золотое правило" механики является приближенным законом, так как в нем не учитывается работа по преодолению трения и силы тяжести частей используемых приспособлений. Тем не менее оно бывает очень полезным при анализе работы любого простого механизма.<br> |
| | | | |
| - | Так, например, благодаря этому правилу мы сразу можем сказать, что рабочему, изображенному на рисунке 47, | + | Так, например, благодаря этому правилу мы сразу можем сказать, что рабочему, изображенному на рисунке 47, [[Image:Pic 47,58.jpg]]при двукратном выигрыше в силе для подъема груза на 10 см придется опустить противоположный конец рычага на 20 см. То же самое будет и в случае, изображенном на рисунке 58. Когда рука человека, держащего веревку, опустится на 20 см, груз, прикрепленный к подвижному блоку, поднимется лишь на 10 см.<br><br>'''??? 1. Почему затраченная при использовании механизмов работа оказывается все время больше полезной работы? 2. Что называют коэффициентом полезного действия механизма? 3. Может ли КПД механизма быть равным 1 (или 100%)? Почему? 4. Каким образом увеличивают КПД? 5. В чем заключается "золотое правило" механики? Кто его автор? 6. Приведите примеры проявления "золотого правила" механики при использовании различных простых механизмов.'''<br><br><br>''С.В. Громов, И.А. Родина, Физика 7 класс'' |
| - | [[Файл:pic_47,58.jpg]]при двукратном выигрыше в силе для подъема груза на 10 см придется опустить противоположный конец рычага на 20 см. То же самое будет и в случае, изображенном на рисунке 58. Когда рука человека, держащего веревку, опустится на 20 см, груз, прикрепленный к подвижному блоку, поднимется лишь на 10 см.<br><br>'''??? 1. Почему затраченная при использовании механизмов работа оказывается все время больше полезной работы? 2. Что называют коэффициентом полезного действия механизма? 3. Может ли КПД механизма быть равным 1 (или 100%)? Почему? 4. Каким образом увеличивают КПД? 5. В чем заключается "золотое правило" механики? Кто его автор? 6. Приведите примеры проявления "золотого правила" механики при использовании различных простых механизмов.'''<br><br><br>''С.В. Громов, И.А. Родина, Физика 7 класс'' | + | |
| | | | |
| - | ''Отослано читателями из интернет-сайтов''<br> | + | ''Отослано читателями из интернет-сайтов''<br> |
| | | | |
| - | | + | <br> <sub>[[Физика 7 класс|Сборник конспектов]] уроков по всем классам, [[Физика и астрономия|рефераты с физики]] 7 класса, книги и [[Гипермаркет знаний - первый в мире!|учебники]] согласно каленадарного планирования физики 7 класса</sub> |
| - | <sub>[[Физика 7 класс|Сборник конспектов]] уроков по всем классам, [[Физика и астрономия|рефераты с физики]] 7 класса, книги и [[Гипермаркет знаний - первый в мире!|учебники]] согласно каленадарного планирования физики 7 класса</sub> | + | |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
Версия 11:39, 9 июня 2010
Гипермаркет знаний>>Физика и астрономия>>Физика 7 класс>>Физика: Коэффициент полезного действия
Используя тот или иной механизм, мы совершаем работу, всегда превышающую ту, которая необходима для достижения поставленной цели. В соответствии с этим различают полную илизатраченную работу Аз и полезную работу Ап . Если, например, наша цель-поднять груз массой ш на высоту Н, то полезная работа - это та, которая обусловлена лишь преодолением силы тяжести, действующей на груз. При равномерном подъеме груза, когда прикладываемая нами сила равна силе тяжести груза, эта работа может быть найдена следующим образом:

Если же мы применяем для подъема груза блок или какой- либо другой механизм, то, кроме силы тяжести груза, нам приходится преодолевать еще и силу тяжести частей механизма, а также действующую в механизме силу трения. Например, используя подвижный блок, мы вынуждены будем совершать дополнительную работу по подъему самого блока с тросом и по преодолению силы трения в оси блока. Кроме того, выигрывая в силе, мы всегда проигрываем в пути (об этом подробнее будет рассказано ниже), что также влияет на работу. Все это приводит к тому, что затраченная нами работа оказывается больше полезной:
Аз > Ап .
Полезная работа всегда составляет лишь некоторую часть полной работы, которую совершает человек, используя механизм.
Физическая величина, показывающая, какую долю составляет полезная работа от всей затраченной работы, называется коэффициентом полезного действия механизма.
Сокращенное обозначение коэффициента полезного действия - КПД.
Чтобы найти КПД механизма, надо полезную работу разделить на ту, которая была затрачена при использовании данного механизма.
Коэффициент полезного действия часто выражают в процентах и обозначают греческой буквой и (читается "эта"):
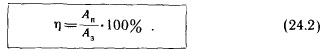
Поскольку числитель Ап в этой формуле всегда меньше знаменателя Аз, то КПД всегда оказывается меньше 1 (или 100%).
Конструируя механизмы, стремятся увеличить их КПД. Для этого уменьшают трение в осях механизмов и их массу. В тех случаях, когда трение ничтожно мало и используемые механизмы имеют массу, пренебрежимо малую по сравнению с массой поднимаемого груза, коэффициент полезного действия оказывается лишь немного меньше 1. В этом случае затраченную работу можно считать примерно равной полезной работе:

Следует помнить, что выигрыша в работе с помощью простого механизма получить нельзя.
Поскольку каждую из работ в равенстве (24.3) можно выразить в виде произведения соответствующей силы на пройденный путь, то это равенство можно переписать так:

Отсюда следует, что,
выигрывая с помощью механизма в силе, мы во столько же раз проигрываем в пути, и наоборот.
Этот закон называют "золотым правилом" механики. Его автором является древнегреческий ученый Герон Александрийский, живший в I в. н. э.
"Золотое правило" механики является приближенным законом, так как в нем не учитывается работа по преодолению трения и силы тяжести частей используемых приспособлений. Тем не менее оно бывает очень полезным при анализе работы любого простого механизма.
Так, например, благодаря этому правилу мы сразу можем сказать, что рабочему, изображенному на рисунке 47, 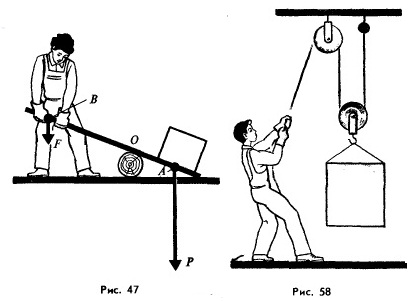 при двукратном выигрыше в силе для подъема груза на 10 см придется опустить противоположный конец рычага на 20 см. То же самое будет и в случае, изображенном на рисунке 58. Когда рука человека, держащего веревку, опустится на 20 см, груз, прикрепленный к подвижному блоку, поднимется лишь на 10 см. при двукратном выигрыше в силе для подъема груза на 10 см придется опустить противоположный конец рычага на 20 см. То же самое будет и в случае, изображенном на рисунке 58. Когда рука человека, держащего веревку, опустится на 20 см, груз, прикрепленный к подвижному блоку, поднимется лишь на 10 см.
??? 1. Почему затраченная при использовании механизмов работа оказывается все время больше полезной работы? 2. Что называют коэффициентом полезного действия механизма? 3. Может ли КПД механизма быть равным 1 (или 100%)? Почему? 4. Каким образом увеличивают КПД? 5. В чем заключается "золотое правило" механики? Кто его автор? 6. Приведите примеры проявления "золотого правила" механики при использовании различных простых механизмов.
С.В. Громов, И.А. Родина, Физика 7 класс
Отослано читателями из интернет-сайтов
Сборник конспектов уроков по всем классам, рефераты с физики 7 класса, книги и учебники согласно каленадарного планирования физики 7 класса
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|