|
|
|
| Строка 5: |
Строка 5: |
| | <br> | | <br> |
| | | | |
| | + | <br> |
| | | | |
| - | | + | '''ПОНЯТИЕ КВАДРАТНОГО КОРНЯ ИЗ НЕОТРИЦАТЕЛЬНОГО ЧИСЛА <br>''' |
| - | '''ПОНЯТИЕ КВАДРАТНОГО КОРНЯ ИЗ НЕОТРИЦАТЕЛЬНОГО ЧИСЛА <br>''' | + | |
| | | | |
| | <br>Рассмотрим уравнение х<sup>2</sup> = 4. Решим его графически. Для этого в одной системе координат построим параболу у = х<sup>2</sup> и прямую у = 4 (рис. 74). Они пересекаются в двух точках А (- 2; 4) и B(2; 4). Абсциссы точек А и В являются корнями уравнения х<sup>2</sup> = 4. Итак, х<sub>1</sub> = - 2, х<sub>2</sub> = 2. | | <br>Рассмотрим уравнение х<sup>2</sup> = 4. Решим его графически. Для этого в одной системе координат построим параболу у = х<sup>2</sup> и прямую у = 4 (рис. 74). Они пересекаются в двух точках А (- 2; 4) и B(2; 4). Абсциссы точек А и В являются корнями уравнения х<sup>2</sup> = 4. Итак, х<sub>1</sub> = - 2, х<sub>2</sub> = 2. |
| | | | |
| - | Рассуждая точно так же, находим корни уравнения х<sup>2</sup> = 9 (см. рис. 74): x<sub>1</sub> = - 3, х<sub>2</sub> = 3. <br> | + | Рассуждая точно так же, находим корни уравнения х<sup>2</sup> = 9 (см. рис. 74): x<sub>1</sub> = - 3, х<sub>2</sub> = 3. <br> |
| | | | |
| - | А теперь попробуем решить уравнение х<sup>2</sup> = 5; геометрическая иллюстрация представлена на рис. 75. Ясно, что это уравнение имеет два корня х<sub>1</sub> и х<sub>2</sub>, причем эти числа, как и в двух предыдущих случаях, равны по абсолютной величине и противоположны по знаку (х<sub>1</sub> — - х<sub>2</sub>)- Но в отличие от предыдущих случаев, где корни уравнения были найдены без труда (причем их можно было найти и не пользуясь графиками), с уравнением х<sup>2</sup> = 5 дело обстоит не так: по чертежу мы не можем указать значения корней, можем только установить, что один корень располагается чуть левее точки - 2, а второй — чуть правее<br> | + | А теперь попробуем решить уравнение х<sup>2</sup> = 5; геометрическая иллюстрация представлена на рис. 75. Ясно, что это уравнение имеет два корня х<sub>1</sub> и х<sub>2</sub>, причем эти числа, как и в двух предыдущих случаях, равны по абсолютной величине и противоположны по знаку (х<sub>1</sub> — - х<sub>2</sub>)- Но в отличие от предыдущих случаев, где корни уравнения были найдены без труда (причем их можно было найти и не пользуясь графиками), с уравнением х<sup>2</sup> = 5 дело обстоит не так: по чертежу мы не можем указать значения корней, можем только установить, что один корень располагается чуть левее точки - 2, а второй — чуть правее<br> |
| | | | |
| - | точки 2. <br> | + | точки 2. <br> |
| | | | |
| - | <br> | + | <br> |
| | | | |
| | [[Image:12-06-11.jpg]]<br><br><br>Что же это за число (точка), которое располагается чуть правее точки 2 и которое в квадрате дает 5? Ясно, что это не 3, так как З<sup>2</sup> = 9, т. е. получается больше, чем нужно (9 > 5). | | [[Image:12-06-11.jpg]]<br><br><br>Что же это за число (точка), которое располагается чуть правее точки 2 и которое в квадрате дает 5? Ясно, что это не 3, так как З<sup>2</sup> = 9, т. е. получается больше, чем нужно (9 > 5). |
| Строка 27: |
Строка 27: |
| | Следовательно, число m<sup>2</sup> оканчивается либо цифрой 5, либо цифрой 0. Но тогда и натуральное число m оканчивается либо цифрой 5, либо цифрой 0, т.е. число m делится на 5 без остатка. Иными словами, если число т разделить на 5, то в частном получится какое-то натуральное число k. Это значит, <br>что m = 5k. <br>А теперь смотрите: <br>m<sup>2</sup> = 5n<sup>2</sup>; <br>Подставим 5k вместо m в первое равенство: | | Следовательно, число m<sup>2</sup> оканчивается либо цифрой 5, либо цифрой 0. Но тогда и натуральное число m оканчивается либо цифрой 5, либо цифрой 0, т.е. число m делится на 5 без остатка. Иными словами, если число т разделить на 5, то в частном получится какое-то натуральное число k. Это значит, <br>что m = 5k. <br>А теперь смотрите: <br>m<sup>2</sup> = 5n<sup>2</sup>; <br>Подставим 5k вместо m в первое равенство: |
| | | | |
| - | (5k)<sup>2</sup> = 5n<sup>2</sup>, т. е. 25k<sup>2</sup> = 5n<sup>2</sup> или n<sup>2</sup> = 5k<sup>2</sup>. <br>Последнее равенство означает, что число. 5n<sup>2</sup> делится на 5 без остатка. Рассуждая, как и выше, приходим к выводу о том, что и число n делится на 5 без остатка. <br>Итак, m делится на 5, n делится на 5, значит, дробь [[Image:12-06-16.jpg]] можно сократить (на 5). Но ведь мы предполагали, что дробь [[Image:12-06-16.jpg]] несократимая. В чем же дело? Почему, правильно рассуждая, мы пришли к абсурду или, как чаще говорят математики, получили противоречие"! Да потому, что неверной была исходная посылка, будто бы существует такая несократимая дробь [[Image:12-06-16.jpg]] , для которой выполняется равенство [[Image:12-06-14.jpg]] <br>Отсюда делаем вывод: такой дроби нет. <br>Метод доказательства, который мы применили только что, называют в математике методом доказательства от противного. Суть его в следующем. Нам нужно доказать некоторое утверждение, а мы предполагаем, что оно не выполняется (математики говорят: «предположим противное» — не в смысле «неприятное», а в смысле «противоположное тому, что требуется"). <br>Если в результате правельных рассуждений приходим к противоречию с условием, то делаем вывод: наше предположение неверно, значит, верно то, что требовалось доказать. | + | (5k)<sup>2</sup> = 5n<sup>2</sup>, т. е. 25k<sup>2</sup> = 5n<sup>2</sup> или n<sup>2</sup> = 5k<sup>2</sup>. <br>Последнее равенство означает, что число. 5n<sup>2</sup> делится на 5 без остатка. Рассуждая, как и выше, приходим к выводу о том, что и число n делится на 5 без остатка. <br>Итак, m делится на 5, n делится на 5, значит, дробь [[Image:12-06-16.jpg]] можно сократить (на 5). Но ведь мы предполагали, что дробь [[Image:12-06-16.jpg]] несократимая. В чем же дело? Почему, правильно рассуждая, мы пришли к абсурду или, как чаще говорят математики, получили противоречие"! Да потому, что неверной была исходная посылка, будто бы существует такая несократимая дробь [[Image:12-06-16.jpg]] , для которой выполняется равенство [[Image:12-06-14.jpg]] <br>Отсюда делаем вывод: такой дроби нет. <br>Метод доказательства, который мы применили только что, называют в математике методом доказательства от противного. Суть его в следующем. Нам нужно доказать некоторое утверждение, а мы предполагаем, что оно не выполняется (математики говорят: «предположим противное» — не в смысле «неприятное», а в смысле «противоположное тому, что требуется"). <br>Если в результате правельных рассуждений приходим к противоречию с условием, то делаем вывод: наше предположение неверно, значит, верно то, что требовалось доказать. |
| | + | |
| | + | Итак, располагая только рациональными числами (а других чисел мы с вами пока не знаем), уравнение х<sup>2</sup> = 5 мы решить не сможем. <br>Встретившись впервые с подобной ситуацией, математики поняли, что надо придумать способ ее описания на математическом языке. Они ввели в рассмотрение новый символ [[Image:12-06-18.jpg]] , который назвали квадратным корнем, и с помощью этого символа корни уравнения х<sup>2</sup> = 5 записали так: [[Image:12-06-19.jpg]] <br>чиется: «корень квадратный из 5"). Теперь для любого уравнения вида х<sup>2</sup> = а, где а > О, можно найти корни — ими являются числа [[Image:12-06-20.jpg]], (рис. 76). |
| | + | |
| | + | [[Image:12-06-21.jpg]] |
| | + | |
| | + | <br>Еще раэ подчеркнем, что число [[Image:12-06-22.jpg]] не целое и не дробь. <br>Значит, [[Image:12-06-22.jpg]] не рациональное число, это число новой природы, о таких числах мы специально поговорим позднее, в главе 5. <br>Пока лишь отметим, что новое число [[Image:12-06-22.jpg]] находится между числами 2 и 3, поскольку 2<sup>2</sup> = 4, а это меньше, чем 5; З<sup>2</sup> = 9, а это больше, чем 5. Можно уточнить: |
| | + | |
| | + | [[Image:12-06-23.jpg]]<br>В самом деле, 2,2<sup>2</sup> = 4,84 < 5, а 2,3<sup>2</sup> = 5,29 > 5. Можно еще <br>уточнить: <br>[[Image:12-06-24.jpg]]<br>действительно, 2,23<sup>2</sup> = 4,9729 < 5, а 2,24<sup>2</sup> = 5,0176 > 5. <br>На практике обычно полагают, что число [[Image:12-06-22.jpg]] равно 2,23 или оно равно 2,24, только это не обычное равенство, а приближенное равенство, для обозначения которого используют символ ». <br>Итак, <br>[[Image:12-06-25.jpg]]<br><br>Обсуждая решение уравнения х<sup>2</sup> = а, мы столкнулись с довольно типичным для математики положением дел. Попадая в нестандартную, нештатную (как любят выражаться космонавты) ситуацию и не найдя выхода из нее с помощью известных средств, математики придумывают для впервые встретившейся им математической модели новый термин и новое обозначение (новый символ); иными словами, они вводят новое понятие, а затем изучают свойства этого <br>понятия. Тем самым новое понятие и его обозначение становятся достоянием математического языка. Мы действовали так же: ввели термин «корень квадратный из числа а», ввели символ [[Image:12-06-26.jpg]] для его обозначения, а чуть позднее изучим свойства нового понятия. Пока мы знаем лишь одно: если а > 0, <br>то [[Image:12-06-26.jpg]] — положительное число, удовлетворяющее уравнению х<sup>2</sup> = а. Иными словами, [[Image:12-06-26.jpg]] — это такое положительное число, при возведении которого в квадрат получается число а. <br>Поскольку уравнение х<sup>2</sup> = 0 имеет корень х = 0, условились считать, что [[Image:12-06-27.jpg]]<br>Теперь мы готовы дать строгое определение. <br>'''''Определение.''''' Квадратным корнем из неотрицательного числа а называют такое неотрицательное число, квадрат которого равен а. |
| | + | |
| | + | Это число обозначают [[Image:12-06-26.jpg]] , число а при этом называют подкоренным числом. <br>Итак, если а — неотрицательное число, то: <br>[[Image:12-06-28.jpg]]<br>Если а < О, то уравнение х<sup>2</sup> = а не имеет корней, говорить в этом случае о квадратном корне из числа а не имеет смысла. <br>Таким образом, выражение [[Image:12-06-26.jpg]] имеет смысл лишь при а > 0. <br>Говорят, что [[Image:12-06-29.jpg]]— одна и та же математическая модель (одна и та же зависимость между неотрицательными числами <br>( а и b), но только вторая описана на более простом языке, чем первая (использует более простые символы). |
| | + | |
| | + | Операцию нахождения квадратного корня из неотрицательного числа называют извлечением квадратного корня. Эта операция является обратной по отношению к возведению в квадрат. Сравните: |
| | + | |
| | + | [[Image:12-06-30.jpg]]<br><br>Еще раз обратите внимание: в таблице фигурируют только положительные числа, поскольку это оговорено в определении квадратного корня. И хотя, например, (- 5)<sup>2</sup> = 25 — верное равенство, перейти от него к записи с использованием квадратного корня (т.е. написать, что .[[Image:12-06-31.jpg]]) <br>нельзя. По определению, .[[Image:12-06-32.jpg]] — положительное число, значит, [[Image:12-06-33.jpg]]. <br>Часто говорят не «квадратный корень», а «арифметический квадратный корень». Термин «арифметический» мы опускаем для краткости. <br>[[Image:12-06-34.jpg]]<br><br>г) В отличие от предыдущих примеров мы не можем указать точное значение числа [[Image:12-06-35.jpg]] . Ясно лишь, что оно больше, чем 4, но меньше, чем 5, поскольку |
| | | | |
| - | <br>Итак, располагая только рациональными числами <br>(а других чисел мы с вами пока не знаем), уравнение х2 = 5 мы <br>решить не сможем. <br>Встретившись впервые с <br>подобной ситуацией, матема- <br>тики поняли, что надо приду- <br>мать способ ее описания на <br>математическом языке. Они <br>ввели в рассмотрение новый <br>символ V , который назвали <br>квадратным корнем, и с по- <br>мощью этого символа корни <br>уравнения х <br>так: хх = <br>ется: «корень квадратный из <br>1 <br>\ <br>\\У <br>\ <br>= х <br>L- <br>V <br>!\ <br>\\ <br>i <br>i <br>ft <br>\ <br>\ <br>У . <br>ч <br>а <br>\ <br>0 <br>_ <br>| <br>/ <br>/ <br>/! <br>/ <br>/ <br>/ <br>¦ <br>Га <br>У <br>= а <br>2 = 5 записали <br>Х2 ~ ~ ft> (чита- <br>пяти»). Теперь для любого <br>ис> уравнения вида х2 — а, где а > О, <br>можно найти корни — ими являются числа Jo, и -Jo, <br>(рис. 76). <br>Еще раэ подчеркнем, что число ^5 не целое и не дробь. <br>Значит, у[Ь — не рациональное число, это <br>число новой природы, о таких числах мы <br>специально поговорим позднее, в главе 5. <br>Пока лишь отметим, что новое число ^5 на- <br>ходится между числами 2 и 3, поскольку 22 = 4, а это меньше, <br>чем 5; З2 = 9, а это больше, чем 5. Можно уточнить: <br>2,2 < Л <2,3. <br>В самом деле, 2,22 = 4,84 < 5, а 2,32 = 5,29 > 5. Можно еще <br>уточнить: <br>2,23 < ^5 < 2,24; <br>действительно, 2,232 = 4,9729 < 5, а 2,242 = 5,0176 > 5. <br>На практике обычно полагают, что число ^5 равно 2,23 <br>или оно равно 2,24, только это не обычное равенство, а при- <br>ближенное равенство, для обозначения которого используют <br>символ ». <br>Итак, <br>^5 ~ 2,23 или ft * 2,24. <br>обратите <br>внимание <br>Обсуждая решение уравнения х2 — а, мы <br>столкнулись с довольно типичным для мате- <br>матики положением дел. Попадая в нестан- <br>дартную, нештатную (как любят выражаться <br>космонавты) ситуацию и не найдя выхода из <br>нее с помощью известных средств, математики придумывают <br>для впервые встретившейся им математической модели новый <br>термин и новое обозначение (новый символ); иными словами, <br>они вводят новое понятие, а затем изучают свойства этого <br>понятия. Тем самым новое понятие и его обозначение <br>становятся достоянием математического языка. Мы действо- <br>вали так же: ввели термин «корень квадратный из числа а», <br>ввели символ ^а для его обозначения, а чуть позднее изучим <br>свойства нового понятия. Пока мы знаем лишь одно: если а > 0, <br>то ^ja — положительное число, удовлетворяющее уравнению <br>х2 = а. Иными словами, ^а — это такое положительное число, <br>при возведении которого в квадрат получается число а. <br>Поскольку уравнение х2 = 0 имеет корень х = 0, условились <br>считать, что ^0 = 0. <br>Теперь мы готовы дать строгое определение. <br>Определение. Квадратным корнем из неотри- <br>цательного числа а называют такое неотрица- <br>тельное число, квадрат которого равен а. Это <br>число обозначают ^[а , число а при этом назы- <br>вают подкоренным числом. <br>Итак, если а — неотрицательное число, то: <br>J = д- ] <br>Если а < О, то уравнение х2 = а не имеет корней, говорить в <br>этом случае о квадратном корне из числа а не имеет смысла. <br>Таким образом, выражение \fa имеет смысл лишь при а > 0. <br>к Говорят, что Jo. = Ъ nb2 = а — одна и та же <br>L математическая модель (одна и та же <br>Ш зависимость между неотрицательными числами <br>* а и Ь), но только вторая описана на более простом <br>языке, чем первая (использует более простые <br>символы). <br>Операцию нахождения квадратного корня <br>из неотрицательного числа называют <br>извлечением квадратного корня. Эта операция <br>является обратной по отношению к возведению <br>в квадрат. Сравните: <br>квадратный <br>корень <br>подкоренное <br>число <br>извлечение <br>квадратного <br>корня <br>Возведение в квадрат <br>52 = 25 <br>102 = 100 <br>0.32 = 0,09 <br>Извлечение квадратного корня <br>,/25 =5 <br>л/ioo =ю <br>VWJ9 =0,3 <br>обратите <br>внимание <br>Еще раз обратите внимание: в таблице <br>фигурируют только положительные числа, <br>поскольку это оговорено в определении квад- <br>ратного корня. И хотя, например, (- 5J = 25 — <br>верное равенство, перейти от него к записи <br>с использованием квадратного корня (т.е. написать, что .^25 = -5) <br>нельзя. По определению, .^25 — положительное число, зна- <br>чит, >/25 = 5 (а не - 5). <br>Часто говорят не «квадратный корень», а «арифметиче- <br>ский квадратный корень». Термин «арифметический» мы <br>опускаем для краткости. <br>e) 7961; <br>Пример 1. Вычислить: <br>а) 749 ; в) ТО ; <br>Решение. <br>а) 749 = 7, поскольку 7 > 0 и 72 = 49. <br>б) 70,25 = 0,5, так как 0,5 > 0 и 0,52 = 0,25. <br>в) ТО = 0. <br>г) В отличие от предыдущих примеров мы не можем ука- <br>зать точное значение числа 7^7 . Ясно лишь, что оно больше, <br>чем 4, но меньше, чем 5, поскольку 42 = 16 (это меньше, чем <br>17), а 52 = 25 (это больше, чем 17). <br>Впрочем, приближенное значение числа 7^7 можно найти <br>с помощью микрокалькулятора, который содержит операцию <br>извлечения квадратного корня; это значение равно 4,123. <br>Итак, 717 * 4,123. <br>Число 7^7 , как и рассмотренное выше <br>число 75 » не является рациональным. <br>обратите <br>внимание <br>д) Вычислить 7~4 нельзя, поскольку квад- <br>ратный корень из отрицательного числа не существует; запись <br>J-4 лишена смысла. Предложенное задание некорректно. <br>е) ^/961 = 31, так как 31 > 0 и 312 = 961. В подобных <br>случаях приходится использовать таблицу квадратов <br>натуральных чисел или микрокалькулятор. <br>ж) .^5625 = 75, поскольку 75 > 0 и 752 = 5625. <Ш <br>В простейших случаях значение квадратного корня <br>вычисляется сразу: дД = 1, ^/4 = 2, ^16 = 4, ^/0,01 = 0,1 и <br>т. д. В более сложных случаях приходится использовать <br>таблицу квадратов чисел или проводить вычисления с <br>помощью микрокалькулятора. А как быть, если под рукой нет <br>ни таблицы, ни калькулятора? Ответим на этот вопрос, решив <br>следующий пример. <br>Пример 2. Вычислить ^2809 . <br>Решение. <br>Первый этап. Нетрудно догадаться, что в ответе получится <br>50 с «хвостиком». В самом деле, 502 = 2500, а 602 = 3600, число <br>же 2809 находится между числами 2500 и 3600. <br>Второй этап. Найдем «хвостик», т.е. последнюю циф- <br>ру искомого числа. Пока мы знаем, что если корень извлека- <br>ется, то в ответе может получиться 51, 52, 53, 54, 55, <br>56, 57, 58 или 59. Проверить надо только два числа: 53 и <br>57, поскольку только они при возведении в квадрат дадут <br>в результате четырехзначное число, оканчивающееся циф- <br>рой 9, т. е. той же цифрой, которой оканчивается число <br>2809. <br>Имеем 532 = 2809 — это то, что нам нужно (нам повезло, <br>мы сразу попали в «яблочко»). Значит, J280! <br>53. <br>Ответ: <br>Пример 3. Катеты прямоугольного треугольника <br>равны 1 см и 2 см. Чему равна гипотенуза треугольника <br>известной из геометрии теоремой <br>Пифагора: сумма квадратов длин <br>катетов прямоугольного тре- <br>угольника равна квадрату длины <br>его гипотенузы, т. е. а2 + Ъ2 = с2, <br>где а, Ъ — катеты, с — гипоте- <br>нуза прямоугольного треуголь- <br>ника. Значит, <br>2 <br>Рис. 77 <br>с- <br>Ответ: <br>см. <br>Этот пример показывает, что введение квадратных корней — <br>не прихоть математиков, а объективная необходимость: в <br>реальной жизни встречаются ситуации, математические <br>модели которых содержат операцию извлечения квадратного <br>корня. Пожалуй, самая важная из таких ситуаций связана с <br>решением квадратных уравнений. До сих пор, встречаясь с <br>квадратными уравнениями ах2 + Ъх + с = 0, мы либо раскла- <br>дывали левую часть на множители (что получалось далеко не <br>всегда), либо использовали графические методы (что тоже не <br>очень надежно, хотя и красиво). На самом деле для отыскания <br>корней хх и хг квадратного уравнения ах2 + Ъх + с = 0 <br>в математике используются формулы <br>содержащие, как видно, знак квадратного <br>корня. Эти формулы применяются на практике <br>следующим образом. Пусть, например, надо решить уравнение <br>2х2 + Ъх - 7 = 0. Здесь а = 2, Ъ = 5, с = - 7. Следовательно, <br>Ъ2 - Аас = 52 - 4 • 2 • (- 7) = 81. Далее находим ^81 = 9. Значит, <br>-5 + 9 <br>2-2 <br>-5-9 <br>Выше мы отметили, что ^5 — не рациональное число. <br>Математики такие числа называют иррациональными. Ирра- <br>циональным является любое число вида Jn , если квадратный <br>корень не извлекается. Например, JH, ,JVf, -/20 и т.д. — <br>иррациональные числа. В главе 5 мы более подробно поговорим <br>о рациональных и иррациональных числах. Рациональные и <br>иррациональные числа вместе составляют множество <br>действительных чисел, т.е. множество всех тех чисел, <br>которыми мы оперируем в реальной жизни (в действитель- <br>ности). Например, -5; 0; 1,3; 3,25; ^5,2 + ,Д , 1 - JTJ — все <br>это действительные числа. <br>Подобно тому, как выше мы определили <br>понятие квадратного корня, можно определить <br>и понятие кубического корня: кубическим <br>корнем из неотрицательного числа а называют <br>такое неотрицательное число, куб которого <br>равен а. Иными словами, равенство %fa = Ъ <br>означает, что Ь3 = а. <br>Например, ^/27 = 3, так как З3 = 27; ^/б4 = 4, так как 43 = 64; <br>^/0,001 = 0,1, так как ОД3 = 0,001. <br>Более того, в математике введено понятие корня п-й <br>степени (л = 2, 3, 4, ...) из неотрицательного числа: если <br>а *> 0, то запись ц[а = Ъ означает, что Ъ > 0 и b" = а. Например, <br>^/81 = 3, так как 3 > 0 и З4 = 81; ^/32 = 2, так как 2 > 0 и 25 = 32. <br>Все это мы будем изучать в курсе алгебры 11-го класса. <br>кубический <br>корень <br><br><br><br><br>89 <br><br><br><br><br>85 <br><br><br>
| + | 4<sup>2</sup> = 16 (это меньше, чем 17), а 5<sup>2</sup> = 25 (это больше, чем 17). <br>Впрочем, приближенное значение числа [[Image:12-06-35.jpg]] можно найти с помощью микрокалькулятора, который содержит операцию извлечения квадратного корня; это значение равно 4,123. <br>Итак, [[Image:12-06-36.jpg]]<br>Число [[Image:12-06-35.jpg]] , как и рассмотренное выше число [[Image:12-06-22.jpg]] » не является рациональным. <br>д) Вычислить [[Image:12-06-37.jpg]] нельзя, поскольку квадратный корень из отрицательного числа не существует; запись [[Image:12-06-37.jpg]] лишена смысла. Предложенное задание некорректно. <br>е) ^/961 = 31, так как 31 > 0 и 312 = 961. В подобных <br>случаях приходится использовать таблицу квадратов <br>натуральных чисел или микрокалькулятор. <br>ж) .^5625 = 75, поскольку 75 > 0 и 752 = 5625. <Ш <br>В простейших случаях значение квадратного корня <br>вычисляется сразу: дД = 1, ^/4 = 2, ^16 = 4, ^/0,01 = 0,1 и <br>т. д. В более сложных случаях приходится использовать <br>таблицу квадратов чисел или проводить вычисления с <br>помощью микрокалькулятора. А как быть, если под рукой нет <br>ни таблицы, ни калькулятора? Ответим на этот вопрос, решив <br>следующий пример. <br>Пример 2. Вычислить ^2809 . <br>Решение. <br>Первый этап. Нетрудно догадаться, что в ответе получится <br>50 с «хвостиком». В самом деле, 502 = 2500, а 602 = 3600, число <br>же 2809 находится между числами 2500 и 3600. <br>Второй этап. Найдем «хвостик», т.е. последнюю циф- <br>ру искомого числа. Пока мы знаем, что если корень извлека- <br>ется, то в ответе может получиться 51, 52, 53, 54, 55, <br>56, 57, 58 или 59. Проверить надо только два числа: 53 и <br>57, поскольку только они при возведении в квадрат дадут <br>в результате четырехзначное число, оканчивающееся циф- <br>рой 9, т. е. той же цифрой, которой оканчивается число <br>2809. <br>Имеем 532 = 2809 — это то, что нам нужно (нам повезло, <br>мы сразу попали в «яблочко»). Значит, J280! <br>53. <br>Ответ: <br>Пример 3. Катеты прямоугольного треугольника <br>равны 1 см и 2 см. Чему равна гипотенуза треугольника <br>известной из геометрии теоремой <br>Пифагора: сумма квадратов длин <br>катетов прямоугольного тре- <br>угольника равна квадрату длины <br>его гипотенузы, т. е. а2 + Ъ2 = с2, <br>где а, Ъ — катеты, с — гипоте- <br>нуза прямоугольного треуголь- <br>ника. Значит, <br>2 <br>Рис. 77 <br>с- <br>Ответ: <br>см. <br>Этот пример показывает, что введение квадратных корней — <br>не прихоть математиков, а объективная необходимость: в <br>реальной жизни встречаются ситуации, математические <br>модели которых содержат операцию извлечения квадратного <br>корня. Пожалуй, самая важная из таких ситуаций связана с <br>решением квадратных уравнений. До сих пор, встречаясь с <br>квадратными уравнениями ах2 + Ъх + с = 0, мы либо раскла- <br>дывали левую часть на множители (что получалось далеко не <br>всегда), либо использовали графические методы (что тоже не <br>очень надежно, хотя и красиво). На самом деле для отыскания <br>корней хх и хг квадратного уравнения ах2 + Ъх + с = 0 <br>в математике используются формулы <br>содержащие, как видно, знак квадратного <br>корня. Эти формулы применяются на практике <br>следующим образом. Пусть, например, надо решить уравнение <br>2х2 + Ъх - 7 = 0. Здесь а = 2, Ъ = 5, с = - 7. Следовательно, <br>Ъ2 - Аас = 52 - 4 • 2 • (- 7) = 81. Далее находим ^81 = 9. Значит, <br>-5 + 9 <br>2-2 <br>-5-9 <br>Выше мы отметили, что ^5 — не рациональное число. <br>Математики такие числа называют иррациональными. Ирра- <br>циональным является любое число вида Jn , если квадратный <br>корень не извлекается. Например, JH, ,JVf, -/20 и т.д. — <br>иррациональные числа. В главе 5 мы более подробно поговорим <br>о рациональных и иррациональных числах. Рациональные и <br>иррациональные числа вместе составляют множество <br>действительных чисел, т.е. множество всех тех чисел, <br>которыми мы оперируем в реальной жизни (в действитель- <br>ности). Например, -5; 0; 1,3; 3,25; ^5,2 + ,Д , 1 - JTJ — все <br>это действительные числа. <br>Подобно тому, как выше мы определили <br>понятие квадратного корня, можно определить <br>и понятие кубического корня: кубическим <br>корнем из неотрицательного числа а называют <br>такое неотрицательное число, куб которого <br>равен а. Иными словами, равенство %fa = Ъ <br>означает, что Ь3 = а. <br>Например, ^/27 = 3, так как З3 = 27; ^/б4 = 4, так как 43 = 64; <br>^/0,001 = 0,1, так как ОД3 = 0,001. <br>Более того, в математике введено понятие корня п-й <br>степени (л = 2, 3, 4, ...) из неотрицательного числа: если <br>а *> 0, то запись ц[а = Ъ означает, что Ъ > 0 и b" = а. Например, <br>^/81 = 3, так как 3 > 0 и З4 = 81; ^/32 = 2, так как 2 > 0 и 25 = 32. <br>Все это мы будем изучать в курсе алгебры 11-го класса. <br>кубический <br>корень <br><br><br><br><br>89 <br><br><br><br><br>85 <br><br><br> |
| | | | |
| - | <br> | + | <br> |
| | | | |
| | <sub>Помощь школьнику [[Гипермаркет знаний - первый в мире!|онлайн]], Математика для 8 класса [[Математика|скачать]], календарно-тематическое планирование</sub> | | <sub>Помощь школьнику [[Гипермаркет знаний - первый в мире!|онлайн]], Математика для 8 класса [[Математика|скачать]], календарно-тематическое планирование</sub> |
Версия 18:37, 12 июня 2010
Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика:Понятие квадратного корня из неотрицательного числа
ПОНЯТИЕ КВАДРАТНОГО КОРНЯ ИЗ НЕОТРИЦАТЕЛЬНОГО ЧИСЛА
Рассмотрим уравнение х2 = 4. Решим его графически. Для этого в одной системе координат построим параболу у = х2 и прямую у = 4 (рис. 74). Они пересекаются в двух точках А (- 2; 4) и B(2; 4). Абсциссы точек А и В являются корнями уравнения х2 = 4. Итак, х1 = - 2, х2 = 2.
Рассуждая точно так же, находим корни уравнения х2 = 9 (см. рис. 74): x1 = - 3, х2 = 3.
А теперь попробуем решить уравнение х2 = 5; геометрическая иллюстрация представлена на рис. 75. Ясно, что это уравнение имеет два корня х1 и х2, причем эти числа, как и в двух предыдущих случаях, равны по абсолютной величине и противоположны по знаку (х1 — - х2)- Но в отличие от предыдущих случаев, где корни уравнения были найдены без труда (причем их можно было найти и не пользуясь графиками), с уравнением х2 = 5 дело обстоит не так: по чертежу мы не можем указать значения корней, можем только установить, что один корень располагается чуть левее точки - 2, а второй — чуть правее
точки 2.
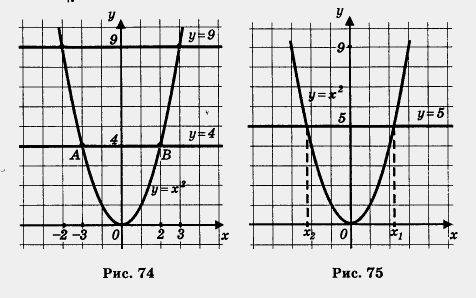
Что же это за число (точка), которое располагается чуть правее точки 2 и которое в квадрате дает 5? Ясно, что это не 3, так как З2 = 9, т. е. получается больше, чем нужно (9 > 5).
Значит, интересующее нас число расположено между числами 2 и 3. Но между числами 2 и 3 находится бесконечное множество рациональных чисел, например 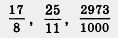 и т. д. Может быть, среди них найдется такая дробь и т. д. Может быть, среди них найдется такая дробь 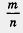 , что , что 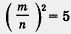 ? Тогда никаких проблем с уравнением х2 — 5 у нас не будет, мы сможем написать, что ? Тогда никаких проблем с уравнением х2 — 5 у нас не будет, мы сможем написать, что 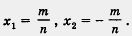
Но тут нас ждет неприятный сюрприз. Оказывается, нет такой дроби 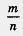 , для которой выполняется равенство , для которой выполняется равенство 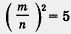
Доказательство сформулированного утверждения довольно сложно. Тем не менее мы его приводим, поскольку оно красиво и поучительно, очень полезно попытаться его понять.
Предположим, что имеется такая несократимая дробь 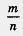 , для которой выполняется равенство , для которой выполняется равенство 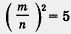 . Тогда . Тогда 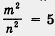 , т. е. m2 = 5n2. Последнее равенство означает, что натуральное число m2 делится без остатка на 5 (в частном получится п2). , т. е. m2 = 5n2. Последнее равенство означает, что натуральное число m2 делится без остатка на 5 (в частном получится п2).
Следовательно, число m2 оканчивается либо цифрой 5, либо цифрой 0. Но тогда и натуральное число m оканчивается либо цифрой 5, либо цифрой 0, т.е. число m делится на 5 без остатка. Иными словами, если число т разделить на 5, то в частном получится какое-то натуральное число k. Это значит,
что m = 5k.
А теперь смотрите:
m2 = 5n2;
Подставим 5k вместо m в первое равенство:
(5k)2 = 5n2, т. е. 25k2 = 5n2 или n2 = 5k2.
Последнее равенство означает, что число. 5n2 делится на 5 без остатка. Рассуждая, как и выше, приходим к выводу о том, что и число n делится на 5 без остатка.
Итак, m делится на 5, n делится на 5, значит, дробь 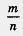 можно сократить (на 5). Но ведь мы предполагали, что дробь можно сократить (на 5). Но ведь мы предполагали, что дробь 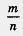 несократимая. В чем же дело? Почему, правильно рассуждая, мы пришли к абсурду или, как чаще говорят математики, получили противоречие"! Да потому, что неверной была исходная посылка, будто бы существует такая несократимая дробь несократимая. В чем же дело? Почему, правильно рассуждая, мы пришли к абсурду или, как чаще говорят математики, получили противоречие"! Да потому, что неверной была исходная посылка, будто бы существует такая несократимая дробь 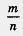 , для которой выполняется равенство , для которой выполняется равенство 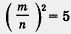
Отсюда делаем вывод: такой дроби нет.
Метод доказательства, который мы применили только что, называют в математике методом доказательства от противного. Суть его в следующем. Нам нужно доказать некоторое утверждение, а мы предполагаем, что оно не выполняется (математики говорят: «предположим противное» — не в смысле «неприятное», а в смысле «противоположное тому, что требуется").
Если в результате правельных рассуждений приходим к противоречию с условием, то делаем вывод: наше предположение неверно, значит, верно то, что требовалось доказать.
Итак, располагая только рациональными числами (а других чисел мы с вами пока не знаем), уравнение х2 = 5 мы решить не сможем.
Встретившись впервые с подобной ситуацией, математики поняли, что надо придумать способ ее описания на математическом языке. Они ввели в рассмотрение новый символ 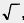 , который назвали квадратным корнем, и с помощью этого символа корни уравнения х2 = 5 записали так: , который назвали квадратным корнем, и с помощью этого символа корни уравнения х2 = 5 записали так: 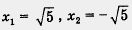
чиется: «корень квадратный из 5"). Теперь для любого уравнения вида х2 = а, где а > О, можно найти корни — ими являются числа 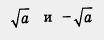 , (рис. 76). , (рис. 76).
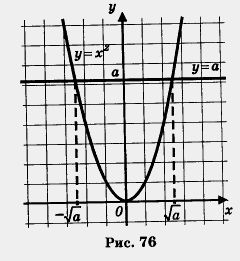
Еще раэ подчеркнем, что число 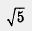 не целое и не дробь. не целое и не дробь.
Значит, 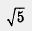 не рациональное число, это число новой природы, о таких числах мы специально поговорим позднее, в главе 5. не рациональное число, это число новой природы, о таких числах мы специально поговорим позднее, в главе 5.
Пока лишь отметим, что новое число 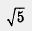 находится между числами 2 и 3, поскольку 22 = 4, а это меньше, чем 5; З2 = 9, а это больше, чем 5. Можно уточнить: находится между числами 2 и 3, поскольку 22 = 4, а это меньше, чем 5; З2 = 9, а это больше, чем 5. Можно уточнить:
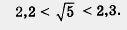
В самом деле, 2,22 = 4,84 < 5, а 2,32 = 5,29 > 5. Можно еще
уточнить:
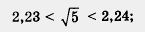
действительно, 2,232 = 4,9729 < 5, а 2,242 = 5,0176 > 5.
На практике обычно полагают, что число 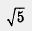 равно 2,23 или оно равно 2,24, только это не обычное равенство, а приближенное равенство, для обозначения которого используют символ ». равно 2,23 или оно равно 2,24, только это не обычное равенство, а приближенное равенство, для обозначения которого используют символ ».
Итак,
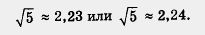
Обсуждая решение уравнения х2 = а, мы столкнулись с довольно типичным для математики положением дел. Попадая в нестандартную, нештатную (как любят выражаться космонавты) ситуацию и не найдя выхода из нее с помощью известных средств, математики придумывают для впервые встретившейся им математической модели новый термин и новое обозначение (новый символ); иными словами, они вводят новое понятие, а затем изучают свойства этого
понятия. Тем самым новое понятие и его обозначение становятся достоянием математического языка. Мы действовали так же: ввели термин «корень квадратный из числа а», ввели символ 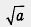 для его обозначения, а чуть позднее изучим свойства нового понятия. Пока мы знаем лишь одно: если а > 0, для его обозначения, а чуть позднее изучим свойства нового понятия. Пока мы знаем лишь одно: если а > 0,
то 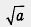 — положительное число, удовлетворяющее уравнению х2 = а. Иными словами, — положительное число, удовлетворяющее уравнению х2 = а. Иными словами, 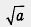 — это такое положительное число, при возведении которого в квадрат получается число а. — это такое положительное число, при возведении которого в квадрат получается число а.
Поскольку уравнение х2 = 0 имеет корень х = 0, условились считать, что 
Теперь мы готовы дать строгое определение.
Определение. Квадратным корнем из неотрицательного числа а называют такое неотрицательное число, квадрат которого равен а.
Это число обозначают 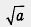 , число а при этом называют подкоренным числом. , число а при этом называют подкоренным числом.
Итак, если а — неотрицательное число, то:
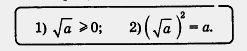
Если а < О, то уравнение х2 = а не имеет корней, говорить в этом случае о квадратном корне из числа а не имеет смысла.
Таким образом, выражение 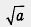 имеет смысл лишь при а > 0. имеет смысл лишь при а > 0.
Говорят, что 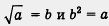 — одна и та же математическая модель (одна и та же зависимость между неотрицательными числами — одна и та же математическая модель (одна и та же зависимость между неотрицательными числами
( а и b), но только вторая описана на более простом языке, чем первая (использует более простые символы).
Операцию нахождения квадратного корня из неотрицательного числа называют извлечением квадратного корня. Эта операция является обратной по отношению к возведению в квадрат. Сравните:
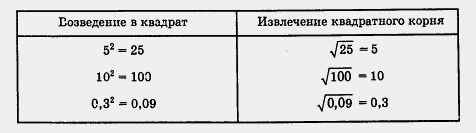
Еще раз обратите внимание: в таблице фигурируют только положительные числа, поскольку это оговорено в определении квадратного корня. И хотя, например, (- 5)2 = 25 — верное равенство, перейти от него к записи с использованием квадратного корня (т.е. написать, что .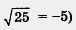 ) )
нельзя. По определению, .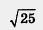 — положительное число, значит, — положительное число, значит, 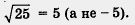 . .
Часто говорят не «квадратный корень», а «арифметический квадратный корень». Термин «арифметический» мы опускаем для краткости.

г) В отличие от предыдущих примеров мы не можем указать точное значение числа 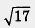 . Ясно лишь, что оно больше, чем 4, но меньше, чем 5, поскольку . Ясно лишь, что оно больше, чем 4, но меньше, чем 5, поскольку
42 = 16 (это меньше, чем 17), а 52 = 25 (это больше, чем 17).
Впрочем, приближенное значение числа 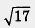 можно найти с помощью микрокалькулятора, который содержит операцию извлечения квадратного корня; это значение равно 4,123. можно найти с помощью микрокалькулятора, который содержит операцию извлечения квадратного корня; это значение равно 4,123.
Итак, 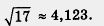
Число 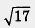 , как и рассмотренное выше число , как и рассмотренное выше число 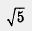 » не является рациональным. » не является рациональным.
д) Вычислить 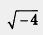 нельзя, поскольку квадратный корень из отрицательного числа не существует; запись нельзя, поскольку квадратный корень из отрицательного числа не существует; запись 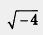 лишена смысла. Предложенное задание некорректно. лишена смысла. Предложенное задание некорректно.
е) ^/961 = 31, так как 31 > 0 и 312 = 961. В подобных
случаях приходится использовать таблицу квадратов
натуральных чисел или микрокалькулятор.
ж) .^5625 = 75, поскольку 75 > 0 и 752 = 5625. <Ш
В простейших случаях значение квадратного корня
вычисляется сразу: дД = 1, ^/4 = 2, ^16 = 4, ^/0,01 = 0,1 и
т. д. В более сложных случаях приходится использовать
таблицу квадратов чисел или проводить вычисления с
помощью микрокалькулятора. А как быть, если под рукой нет
ни таблицы, ни калькулятора? Ответим на этот вопрос, решив
следующий пример.
Пример 2. Вычислить ^2809 .
Решение.
Первый этап. Нетрудно догадаться, что в ответе получится
50 с «хвостиком». В самом деле, 502 = 2500, а 602 = 3600, число
же 2809 находится между числами 2500 и 3600.
Второй этап. Найдем «хвостик», т.е. последнюю циф-
ру искомого числа. Пока мы знаем, что если корень извлека-
ется, то в ответе может получиться 51, 52, 53, 54, 55,
56, 57, 58 или 59. Проверить надо только два числа: 53 и
57, поскольку только они при возведении в квадрат дадут
в результате четырехзначное число, оканчивающееся циф-
рой 9, т. е. той же цифрой, которой оканчивается число
2809.
Имеем 532 = 2809 — это то, что нам нужно (нам повезло,
мы сразу попали в «яблочко»). Значит, J280!
53.
Ответ:
Пример 3. Катеты прямоугольного треугольника
равны 1 см и 2 см. Чему равна гипотенуза треугольника
известной из геометрии теоремой
Пифагора: сумма квадратов длин
катетов прямоугольного тре-
угольника равна квадрату длины
его гипотенузы, т. е. а2 + Ъ2 = с2,
где а, Ъ — катеты, с — гипоте-
нуза прямоугольного треуголь-
ника. Значит,
2
Рис. 77
с-
Ответ:
см.
Этот пример показывает, что введение квадратных корней —
не прихоть математиков, а объективная необходимость: в
реальной жизни встречаются ситуации, математические
модели которых содержат операцию извлечения квадратного
корня. Пожалуй, самая важная из таких ситуаций связана с
решением квадратных уравнений. До сих пор, встречаясь с
квадратными уравнениями ах2 + Ъх + с = 0, мы либо раскла-
дывали левую часть на множители (что получалось далеко не
всегда), либо использовали графические методы (что тоже не
очень надежно, хотя и красиво). На самом деле для отыскания
корней хх и хг квадратного уравнения ах2 + Ъх + с = 0
в математике используются формулы
содержащие, как видно, знак квадратного
корня. Эти формулы применяются на практике
следующим образом. Пусть, например, надо решить уравнение
2х2 + Ъх - 7 = 0. Здесь а = 2, Ъ = 5, с = - 7. Следовательно,
Ъ2 - Аас = 52 - 4 • 2 • (- 7) = 81. Далее находим ^81 = 9. Значит,
-5 + 9
2-2
-5-9
Выше мы отметили, что ^5 — не рациональное число.
Математики такие числа называют иррациональными. Ирра-
циональным является любое число вида Jn , если квадратный
корень не извлекается. Например, JH, ,JVf, -/20 и т.д. —
иррациональные числа. В главе 5 мы более подробно поговорим
о рациональных и иррациональных числах. Рациональные и
иррациональные числа вместе составляют множество
действительных чисел, т.е. множество всех тех чисел,
которыми мы оперируем в реальной жизни (в действитель-
ности). Например, -5; 0; 1,3; 3,25; ^5,2 + ,Д , 1 - JTJ — все
это действительные числа.
Подобно тому, как выше мы определили
понятие квадратного корня, можно определить
и понятие кубического корня: кубическим
корнем из неотрицательного числа а называют
такое неотрицательное число, куб которого
равен а. Иными словами, равенство %fa = Ъ
означает, что Ь3 = а.
Например, ^/27 = 3, так как З3 = 27; ^/б4 = 4, так как 43 = 64;
^/0,001 = 0,1, так как ОД3 = 0,001.
Более того, в математике введено понятие корня п-й
степени (л = 2, 3, 4, ...) из неотрицательного числа: если
а *> 0, то запись ц[а = Ъ означает, что Ъ > 0 и b" = а. Например,
^/81 = 3, так как 3 > 0 и З4 = 81; ^/32 = 2, так как 2 > 0 и 25 = 32.
Все это мы будем изучать в курсе алгебры 11-го класса.
кубический
корень
89
85
Помощь школьнику онлайн, Математика для 8 класса скачать, календарно-тематическое планирование
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|