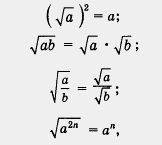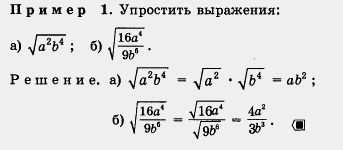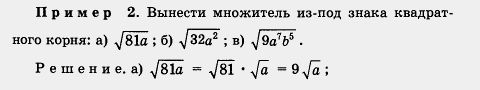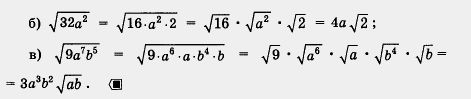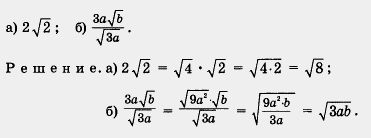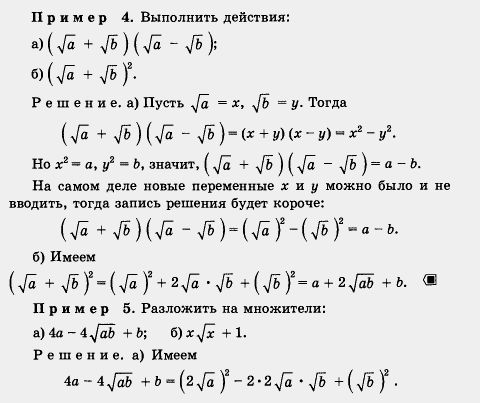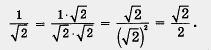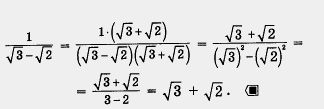|
|
| Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Преобразование выражений, содержащих операцию извлечения квадратного корня</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Преобразование выражений, содержащих операцию извлечения квадратного корня, рациональных выражений, формулы, знаменатель, квадратного корня</metakeywords> |
| | | | |
| - | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика:Преобразование выражений, содержащих операцию извлечения квадратного корня''' | + | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика:Преобразование выражений, содержащих операцию извлечения квадратного корня'''<br> |
| | | | |
| - | <br> | + | <br> '''Преобразование выражений, содержащих операцию извлечения квадратного корня''' |
| | | | |
| | + | <br>До сих пор мы с вами выполняли преобразования только '''[[Преобразование рациональных выражений|рациональных выражений]]''', используя для этого правила действий над многочленами и алгебраическими дробями, формулы сокращенного умножения и т. д. В этой главе мы ввели новую операцию — операцию извлечения квадратного корня; мы установили, что |
| | | | |
| | + | [[Image:12-06-87.jpg|180px|Преобразование выражений]]<br><br>где, напомним, a, b — неотрицательные числа. |
| | | | |
| - | <br> '''ПРЕОБРАЗОВАНИЕ ВЫРАЖЕНИЙ, СОДЕРЖАЩИХ ОПЕРАЦИЮ ИЗВЛЕЧЕНИЯ КВАДРАТНОГО КОРНЯ'''
| + | Используя эти '''[[Конспект уроку на тему «Формула коренів квадратного рівняння»|формулы]]''', можно выполнять различные преобразования выражений, содержащих операцию извлечения квадратного корня. Рассмотрим несколько примеров, причем во всех примерах будем предполагать, что переменные принимают только неотрицательные значения. |
| | | | |
| - | <br>До сих пор мы с вами выполняли преобразования только рациональных выражений, используя для этого правила действий над многочленами и алгебраическими дробями, формулы сокращенного умножения и т. д. В этой главе мы ввели новую операцию — операцию извлечения квадратного корня; мы установили, что
| + | [[Image:12-06-88.jpg|320px|Задание]] |
| | | | |
| - | [[Image:12-06-87.jpg]]<br><br>где, напомним, a, b — неотрицательные числа. <br>Используя эти формулы, можно выполнять различные преобразования выражений, содержащих операцию извлечения квадратного корня. Рассмотрим несколько примеров, причем во всех примерах будем предполагать, что переменные принимают только неотрицательные значения. | + | [[Image:12-06-89.jpg|480px|Задание]] |
| | | | |
| - | [[Image:12-06-88.jpg]] | + | [[Image:12-06-90.jpg|480px|Задание]]<br><br>'''Пример 3.''' Внести множитель под знак квадратного корня: |
| | | | |
| - | [[Image:12-06-89.jpg]] | + | [[Image:12-06-91.jpg|480px|Задание]]<br> |
| | | | |
| - | [[Image:12-06-90.jpg]]<br><br>'''Пример 3.''' Внести множитель под знак квадратного корня: | + | [[Image:12-06-92.jpg|480px|Задание]] |
| | | | |
| - | [[Image:12-06-91.jpg]]<br> | + | [[Image:12-06-93.jpg|480px|Задание]]<br><br>'''Пример 6'''. Упростить выражение Решение. Выполним последовательные преобразования: |
| | | | |
| - | [[Image:12-06-92.jpg]] | + | [[Image:12-06-94.jpg|480px|Задание]]<br> |
| | | | |
| - | [[Image:12-06-93.jpg]]<br><br>'''Пример 6'''. Упростить выражение <br>Решение. Выполним последовательные преобразования: | + | [[Image:12-06-95.jpg|320px|Задание]] |
| | | | |
| - | [[Image:12-06-94.jpg]]<br> | + | '''<br>Пример 7.''' Преобразовать заданное алгебраическое выражение к такому виду, чтобы '''[[Задачі до уроку на тему «Додавання і віднімання дробів з різними знаменниками»|знаменатель]]''' дроби не содержал знаков квадратных корней: |
| | | | |
| - | [[Image:12-06-95.jpg]]
| + | [[Image:12-06-96.jpg|240px|Задание]] |
| - | | + | |
| - | '''<br>Пример 7.''' Преобразовать заданное алгебраическое выражение к такому виду, чтобы знаменатель дроби не содержал знаков квадратных корней:
| + | |
| - | | + | |
| - | [[Image:12-06-96.jpg]] | + | |
| | | | |
| | Решение. В обоих случаях воспользуемся к тем, что значение дроби не изменится, если ее числитель и знаменатель одновременно умножить на одно и то же отличное от нуля число или выражение. | | Решение. В обоих случаях воспользуемся к тем, что значение дроби не изменится, если ее числитель и знаменатель одновременно умножить на одно и то же отличное от нуля число или выражение. |
| Строка 37: |
Строка 35: |
| | а) Умножив числитель и знаменатель дроби на [[Image:12-06-97.jpg]] , получим | | а) Умножив числитель и знаменатель дроби на [[Image:12-06-97.jpg]] , получим |
| | | | |
| - | [[Image:12-06-98.jpg]]<br><br>б) Умножив числитель и знаменатель дроби на [[Image:12-06-99.jpg]]<br>получим | + | [[Image:12-06-98.jpg]]<br><br>б) Умножив числитель и знаменатель дроби на [[Image:12-06-99.jpg|Задание]] получим |
| | | | |
| - | [[Image:12-06-100.jpg]]<br><br>Если знаменатель алгебраической дроби содержит знак квадратного корня, то обычно говорят, что в знаменателе содержится иррациональность (почему используется именно такой термин, мы обсудим позднее, в § 27). | + | [[Image:12-06-100.jpg|320px|Задание]]<br><br>Если знаменатель алгебраической дроби содержит знак '''[[Квадратний корінь. Арифметичний квадратний корінь.|квадратного корня]]''', то обычно говорят, что в знаменателе содержится иррациональность (почему используется именно такой термин, мы обсудим позднее, в § 27). |
| | | | |
| - | Преобразование выражения к такому виду, чтобы в знаменателе дроби не оказалось знаков квадратных корней, называют обычно освобождением от иррациональности в знаменателе. Два основных приема освобождения от иррациональности в знаменателе мы как раз и рассмотрели в примере если знаменатель имеет вид [[Image:12-06-101.jpg]], то числитель и знаменатель дроби следует умножить на[[Image:12-06-101.jpg]] если знаменатель имеет вид [[Image:12-06-102.jpg]] , то числитель и знаменатель дроби надо умножить соответственно на [[Image:12-06-102.jpg]] . <br>Зачем нужно уметь освобождаться от иррациональности в знаменателе? Во многих случаях это облегчает тождественные преобразования алгебраических выражений, в чем мы сейчас и убедимся. | + | Преобразование выражения к такому виду, чтобы в знаменателе дроби не оказалось знаков квадратных корней, называют обычно освобождением от иррациональности в знаменателе. Два основных приема освобождения от иррациональности в знаменателе мы как раз и рассмотрели в примере если знаменатель имеет вид [[Image:12-06-101.jpg]], то числитель и знаменатель дроби следует умножить на[[Image:12-06-101.jpg]] если знаменатель имеет вид [[Image:12-06-102.jpg|180px|Задание]] , то числитель и знаменатель дроби надо умножить соответственно на [[Image:12-06-102.jpg|180px|Задание]] . |
| | + | |
| | + | <br>Зачем нужно уметь освобождаться от иррациональности в знаменателе? Во многих случаях это облегчает тождественные преобразования алгебраических выражений, в чем мы сейчас и убедимся. |
| | | | |
| | '''Пример 8. '''Упростить выражение | | '''Пример 8. '''Упростить выражение |
| | | | |
| - | [[Image:12-06-103.jpg]]<br> | + | [[Image:12-06-103.jpg|480px|Задание]]<br> |
| | | | |
| | + | ''Мордкович А. Г., [http://xvatit.com/vuzi/ '''Алгебра''']. 8 кл.: Учеб. для общеобразоват. учреждений.— 3-е изд., доработ. — М.: Мнемозина, 2001. — 223 с: ил. '' |
| | | | |
| | + | <br> |
| | | | |
| | <sub>Материалы по математике за 8 класс [[Математика|скачать]], конспект по математике , учебники и книги скатать бесплатно, школьная программа [[Гипермаркет знаний - первый в мире!|онлайн]]</sub> <br> | | <sub>Материалы по математике за 8 класс [[Математика|скачать]], конспект по математике , учебники и книги скатать бесплатно, школьная программа [[Гипермаркет знаний - первый в мире!|онлайн]]</sub> <br> |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | '''<u></u>''' | | '''<u></u>''' |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Решение. В обоих случаях воспользуемся к тем, что значение дроби не изменится, если ее числитель и знаменатель одновременно умножить на одно и то же отличное от нуля число или выражение.
Преобразование выражения к такому виду, чтобы в знаменателе дроби не оказалось знаков квадратных корней, называют обычно освобождением от иррациональности в знаменателе. Два основных приема освобождения от иррациональности в знаменателе мы как раз и рассмотрели в примере если знаменатель имеет вид 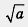 , то числитель и знаменатель дроби следует умножить на
, то числитель и знаменатель дроби следует умножить на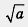 если знаменатель имеет вид
если знаменатель имеет вид 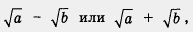 , то числитель и знаменатель дроби надо умножить соответственно на
, то числитель и знаменатель дроби надо умножить соответственно на 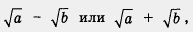 .
.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.