|
|
|
| Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Иррациональные числа</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Иррациональные числа, рациональными, иррациональное число, десятичная дробь, окружности, обыкновенная дробь, операция</metakeywords> |
| | | | |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика:Иррациональные числа''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика:Иррациональные числа''' |
| | | | |
| - | <br> | + | <br>'''Иррациональные числа''' |
| | | | |
| | + | <br>Мы уже неоднократно отмечали, что не все числа, с которыми приходится встречаться в реальной жизни, являются '''[[Презентація уроку: Множення раціональних чисел|рациональными]]'''. Так, не является рациональным числом длина гипотенузы прямоугольного треугольника с катетами 1 см и 2 см: в самом деле, длина с гипотенузы этого треугольника и длины катетов связаны, по теореме Пифагора, соотношением с<sup>2</sup> = I<sup>2</sup> + 2<sup>2</sup>. Значит, с = [[Image:14-06-113.jpg|Число]] см, а [[Image:14-06-113.jpg]] - не рациональное число. Корни уравнения х<sup>2</sup> = 7 также не являются рациональными числами — это числа [[Image:14-06-114.jpg|Число]] и -[[Image:14-06-114.jpg]] . Что же это за числа, которые не являются рациональными? |
| | | | |
| | + | Прежде всего заметим, что в математике не принято говорить «нерациональное число», обычно используют термин '''[[Ірраціональні числа. Дійсні числа|иррациональное число]]'''. Термины «рациональное число», «иррациональное число» происходят от латинского слова ratio — «разум» (буквальный перевод: «рациональное число — разумное число», «иррациональное число — неразумное число»; впрочем, так говорят и в реальной жизни: «он поступил рационально» — это значит, что он поступил разумно; «так действовать нерационально» — это значит, что так действовать неразумно). |
| | | | |
| - | <br>''' ИРРАЦИОНАЛЬНЫЕ ЧИСЛА'''
| + | Рассмотрим уже известное нам иррациональное число [[Image:14-06-113.jpg]]. В § 15 мы отмечали, что оно заключено между числами 2 и 3; если точнее, то между числами 2,2 и 2,3; если еще точнее, — то между числами 2,23 и 2,24. Можно продолжить уточнения оценок числа [[Image:14-06-113.jpg|Число]] и определить границы для третьего десятичного знака после запятой. Имеем 2,2362 = 4,999696, что меньше 5; 2,2372 = = 5,004167, что больше 5. |
| | | | |
| - | <br>Мы уже неоднократно отмечали, что не все числа, с которыми приходится встречаться в реальной жизни, являются рациональными. Так, не является рациональным числом длина гипотенузы прямоугольного треугольника с катетами 1 см и 2 см: в самом деле, длина с гипотенузы этого треугольника и длины катетов связаны, по теореме Пифагора, соотношением с<sup>2</sup> = I<sup>2</sup> + 2<sup>2</sup>. Значит, с = [[Image:14-06-113.jpg]] см, а [[Image:14-06-113.jpg]] - не рациональное число. Корни уравнения х<sup>2</sup> = 7 также не являются рациональными числами — это числа [[Image:14-06-114.jpg]] и -[[Image:14-06-114.jpg]] . Что же это за числа, которые не являются рациональными? <br>Прежде всего заметим, что в математике не принято говорить «нерациональное число», обычно используют термин иррациональное число. Термины «рациональное число», «иррациональное число» происходят от латинского слова ratio — «разум» (буквальный перевод: «рациональное число — разумное число», «иррациональное число — неразумное число»; впрочем, так говорят и в реальной жизни: «он поступил рационально» — это значит, что он поступил разумно; «так действовать нерационально» — это значит, что так действовать неразумно).
| + | Итак, 2,236 < [[Image:14-06-113.jpg]] < 2,237. |
| | | | |
| - | Рассмотрим уже известное нам иррациональное число [[Image:14-06-113.jpg]]. В § 15 мы отмечали, что оно заключено между числами 2 и 3; если точнее, то между числами 2,2 и 2,3; если еще точнее, — то между числами 2,23 и 2,24. Можно продолжить уточнения оценок числа [[Image:14-06-113.jpg]] и определить границы для третьего десятичного <br>знака после запятой. Имеем 2,2362 = 4,999696, что меньше 5; 2,2372 = = 5,004167, что больше 5.
| + | Точно так же можно определить границы для четвертого знака после запятой, для пятого знака и т. д. Ясно, что выполняется приближенное равенство[[Image:14-06-113.jpg|Число]] [[Image:14-06-117.jpg]] 2,236. Если же считать, что для числа [[Image:14-06-113.jpg|Число]] выписаны все последующие десятичные знаки, то можно воспользоваться записью [[Image:14-06-113.jpg]] = 2,236... . Это — бесконечная '''[[Задачі до уроку «Порівняння десяткових дробів.»|десятичная дробь]]'''. В предыдущем параграфе мы уже встречались с бесконечными десятичными дробями, но все они были периодическими и выражали рациональные числа. Иррациональное число [[Image:14-06-113.jpg|Число]] выражается бесконечной десятичной непериодической дробью. |
| | | | |
| - | Итак, 2,236 < [[Image:14-06-113.jpg]] < 2,237. <br>Точно так же можно определить границы для четвертого знака после запятой, для пятого знака и т. д. Ясно, что выполняется приближенное равенство
| + | Вообще, иррациональным числом называют бесконечную десятичную непериодическую дробь. |
| | | | |
| - | [[Image:14-06-113.jpg]] [[Image:14-06-117.jpg]] 2,236. Если же считать, что для числа [[Image:14-06-113.jpg]] выписаны все последующие десятичные знаки, то можно воспользоваться записью [[Image:14-06-113.jpg]] = 2,236... . Это — бесконечная десятичная дробь. В предыдущем параграфе мы уже встречались с бесконечными десятичными дробями, но все они были периодическими и выражали рациональные числа. Иррациональное число [[Image:14-06-113.jpg]] выражается бесконечной десятичной непериодической дробью. <br>Вообще, иррациональным числом называют бесконечную десятичную непериодическую дробь. <br>Такие числа встречаются не только при извлечении квадратного корня, но и во многих других случаях, в чем вы не раз убедитесь в старших классах. <br>
| + | Такие числа встречаются не только при извлечении квадратного корня, но и во многих других случаях, в чем вы не раз убедитесь в старших классах. <br> |
| | | | |
| - | Пока приведем только один пример. Если длину любой окружности разделить на ее диаметр, то в частном получится иррациональное число 3,141592... . Этот факт установил еще в III веке до н. э. греческий математик и философ Архимед. Для указанного числа в математике введено специальное обозначение % (буква греческого алфавита «пи»). <br> | + | Пока приведем только один пример. Если длину любой '''[[2. Числовая окружность|окружности]]''' разделить на ее диаметр, то в частном получится иррациональное число 3,141592... . Этот факт установил еще в III веке до н. э. греческий математик и философ Архимед. Для указанного числа в математике введено специальное обозначение % (буква греческого алфавита «пи»). <br> |
| | | | |
| - | Любая арифметическая операция над рациональными числами приводит в результате к рациональному числу. Это и понятно, ведь сумма (разность, произведение, частное) обыкновенных дробей есть обыкновенная дробь (все логично, ведь рациональные числа — «разумные» числа). А как обстоит дело с <br>иррациональными числами? Оказывается, ничего определенного сказать нельзя (что тоже логично, ведь иррациональные числа — «неразумные» числа). Смотрите: [[Image:14-06-113.jpg]] — иррациональное число, [[Image:14-06-113.jpg]] '''.''' [[Image:14-06-113.jpg]] =5 — рациональное число, т. е. произведение двух иррациональных чисел оказалось рациональным числом; <br>[[Image:14-06-115.jpg]] — иррациональные числа, и их произведение, т. е. [[Image:14-06-116.jpg]] — тоже иррациональное число. То же относится к сложению, вычитанию, делению иррациональных чисел: в ответе может получиться как рациональное, так и иррациональное число. <br> | + | Любая арифметическая операция над рациональными числами приводит в результате к рациональному числу. Это и понятно, ведь сумма (разность, произведение, частное) обыкновенных дробей есть '''[[Задачі до уроку «Додавання і віднімання звичайних дробів з однаковими знаменниками.»|обыкновенная дробь]]''' (все логично, ведь рациональные числа — «разумные» числа). А как обстоит дело с иррациональными числами? Оказывается, ничего определенного сказать нельзя (что тоже логично, ведь иррациональные числа — «неразумные» числа). Смотрите: [[Image:14-06-113.jpg]] — иррациональное число, [[Image:14-06-113.jpg]] '''.''' [[Image:14-06-113.jpg]] =5 — рациональное число, т. е. произведение двух иррациональных чисел оказалось рациональным числом; |
| | | | |
| - | А что получится, если в операции участвуют одно рациональное число и одно иррациональное число, какое «пересилит»? <br>Оказывается, «пересилит» иррациональное число. Рассмотрим такой пример: дано рациональное число 3 и иррациональное число [[Image:14-06-118.jpg]] ;<br>
| + | [[Image:14-06-115.jpg|Числа]] — иррациональные числа, и их произведение, т. е. [[Image:14-06-116.jpg|Число]] — тоже иррациональное число. То же относится к сложению, вычитанию, делению иррациональных чисел: в ответе может получиться как рациональное, так и иррациональное число. <br> |
| | | | |
| - | составим их сумму 3 + [[Image:14-06-118.jpg]] • Предположим, что это — рациональное число r, т. е. 3 + [[Image:14-06-118.jpg]] = г. Тогда [[Image:14-06-118.jpg]] = г - 3, а r - 3 — рациональное число (как разность двух рациональных чисел). Получается, что [[Image:14-06-118.jpg]] — рациональное число, а это неверно, ведь мы знаем, что это число — иррациональное. <br>Получили противоречие, значит, сделанное нами предположение неверно, т. е. 3 + [[Image:14-06-118.jpg]] — иррациональное число. Аналогично можно доказать, что 3-[[Image:14-06-118.jpg]] — иррациональное число. <br>
| + | А что получится, если в операции участвуют одно рациональное число и одно иррациональное число, какое «пересилит»? |
| | | | |
| - | Замечание. Обратите внимание, что в проведенном рассуждении мы снова использовали метод доказательства от противного, о котором в первый раз говорили выше, в § 15. <br>
| + | Оказывается, «пересилит» иррациональное число. Рассмотрим такой пример: дано рациональное число 3 и иррациональное число [[Image:14-06-118.jpg|Число]] ;составим их сумму 3 + [[Image:14-06-118.jpg]] • Предположим, что это — рациональное число r, т. е. 3 + [[Image:14-06-118.jpg|Число]] = г. Тогда [[Image:14-06-118.jpg]] = г - 3, а r - 3 — рациональное число (как разность двух рациональных чисел). Получается, что [[Image:14-06-118.jpg]] — рациональное число, а это неверно, ведь мы знаем, что это число — иррациональное. |
| | | | |
| - | Итак, можно сделать следующие выводы: <br>• Любая арифметическая операция над рациональными числами (кроме деления на 0) приводит в результате к рациональному числу. <br>• Арифметическая операция над иррациональными числами может привести в результате как к рациональному, так и к иррациональному числу. <br>• Если в арифметической операции участвуют рациональное и иррациональное числа, то в результате получится иррациональное число (кроме умножения и деления на 0). <br> | + | Получили противоречие, значит, сделанное нами предположение неверно, т. е. 3 + [[Image:14-06-118.jpg]] — иррациональное число. Аналогично можно доказать, что 3-[[Image:14-06-118.jpg|Число]] — иррациональное число. <br> |
| | + | |
| | + | '''Замечание.''' Обратите внимание, что в проведенном рассуждении мы снова использовали метод доказательства от противного, о котором в первый раз говорили выше, в § 15. <br> |
| | + | |
| | + | |
| | + | |
| | + | <u>'''Итак, можно сделать следующие выводы:'''</u> |
| | + | |
| | + | • Любая арифметическая '''[[Урок 1. Операции|операция]]''' над рациональными числами (кроме деления на 0) приводит в результате к рациональному числу. |
| | + | |
| | + | • Арифметическая операция над иррациональными числами может привести в результате как к рациональному, так и к иррациональному числу. |
| | + | |
| | + | • Если в арифметической операции участвуют рациональное и иррациональное числа, то в результате получится иррациональное число (кроме умножения и деления на 0). <br> |
| | | | |
| | Поскольку операция извлечения квадратного корня из положительного числа часто приводит к иррациональным числам, условились алгебраическое выражение, в котором присутствует операция извлечения квадратного корня, называть иррациональным выражением. | | Поскольку операция извлечения квадратного корня из положительного числа часто приводит к иррациональным числам, условились алгебраическое выражение, в котором присутствует операция извлечения квадратного корня, называть иррациональным выражением. |
| | | | |
| - | Кстати, и термин «освобождение от иррациональности в знаменателе», который мы использовали в § 18, объясняется теми же причинами. <br><br><br><br><br> | + | Кстати, и термин «освобождение от иррациональности в знаменателе», который мы использовали в § 18, объясняется теми же причинами. <br>''<br>Мордкович А. Г., [[Мордкович А. Г., Алгебра. 8 кл.: Учеб. для общеобразоват. учреждений.— 3-е изд., доработ. — М.: Мнемозина, 2001. — 223 с: ил. |'''Алгебра''']]. 8 кл.: Учеб. для общеобразоват. учреждений.— 3-е изд., доработ. — М.: Мнемозина, 2001. — 223 с: ил. ''<br> |
| | | | |
| - | <br> | + | <br> |
| | | | |
| | <sub>Школьная библиотека [[Гипермаркет знаний - первый в мире!|онлайн]], учебники и книги по всему предметам, Математика 8 класс [[Математика|скачать]]</sub> | | <sub>Школьная библиотека [[Гипермаркет знаний - первый в мире!|онлайн]], учебники и книги по всему предметам, Математика 8 класс [[Математика|скачать]]</sub> |
| Строка 40: |
Строка 54: |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | '''<u></u>''' | | '''<u></u>''' |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Версия 13:30, 8 октября 2012
Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика:Иррациональные числа
Иррациональные числа
Мы уже неоднократно отмечали, что не все числа, с которыми приходится встречаться в реальной жизни, являются рациональными. Так, не является рациональным числом длина гипотенузы прямоугольного треугольника с катетами 1 см и 2 см: в самом деле, длина с гипотенузы этого треугольника и длины катетов связаны, по теореме Пифагора, соотношением с2 = I2 + 22. Значит, с = 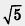 см, а см, а 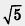 - не рациональное число. Корни уравнения х2 = 7 также не являются рациональными числами — это числа - не рациональное число. Корни уравнения х2 = 7 также не являются рациональными числами — это числа 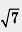 и - и -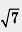 . Что же это за числа, которые не являются рациональными? . Что же это за числа, которые не являются рациональными?
Прежде всего заметим, что в математике не принято говорить «нерациональное число», обычно используют термин иррациональное число. Термины «рациональное число», «иррациональное число» происходят от латинского слова ratio — «разум» (буквальный перевод: «рациональное число — разумное число», «иррациональное число — неразумное число»; впрочем, так говорят и в реальной жизни: «он поступил рационально» — это значит, что он поступил разумно; «так действовать нерационально» — это значит, что так действовать неразумно).
Рассмотрим уже известное нам иррациональное число 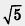 . В § 15 мы отмечали, что оно заключено между числами 2 и 3; если точнее, то между числами 2,2 и 2,3; если еще точнее, — то между числами 2,23 и 2,24. Можно продолжить уточнения оценок числа . В § 15 мы отмечали, что оно заключено между числами 2 и 3; если точнее, то между числами 2,2 и 2,3; если еще точнее, — то между числами 2,23 и 2,24. Можно продолжить уточнения оценок числа 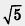 и определить границы для третьего десятичного знака после запятой. Имеем 2,2362 = 4,999696, что меньше 5; 2,2372 = = 5,004167, что больше 5. и определить границы для третьего десятичного знака после запятой. Имеем 2,2362 = 4,999696, что меньше 5; 2,2372 = = 5,004167, что больше 5.
Итак, 2,236 < 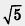 < 2,237. < 2,237.
Точно так же можно определить границы для четвертого знака после запятой, для пятого знака и т. д. Ясно, что выполняется приближенное равенство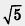 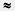 2,236. Если же считать, что для числа 2,236. Если же считать, что для числа 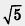 выписаны все последующие десятичные знаки, то можно воспользоваться записью выписаны все последующие десятичные знаки, то можно воспользоваться записью 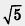 = 2,236... . Это — бесконечная десятичная дробь. В предыдущем параграфе мы уже встречались с бесконечными десятичными дробями, но все они были периодическими и выражали рациональные числа. Иррациональное число = 2,236... . Это — бесконечная десятичная дробь. В предыдущем параграфе мы уже встречались с бесконечными десятичными дробями, но все они были периодическими и выражали рациональные числа. Иррациональное число 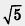 выражается бесконечной десятичной непериодической дробью. выражается бесконечной десятичной непериодической дробью.
Вообще, иррациональным числом называют бесконечную десятичную непериодическую дробь.
Такие числа встречаются не только при извлечении квадратного корня, но и во многих других случаях, в чем вы не раз убедитесь в старших классах.
Пока приведем только один пример. Если длину любой окружности разделить на ее диаметр, то в частном получится иррациональное число 3,141592... . Этот факт установил еще в III веке до н. э. греческий математик и философ Архимед. Для указанного числа в математике введено специальное обозначение % (буква греческого алфавита «пи»).
Любая арифметическая операция над рациональными числами приводит в результате к рациональному числу. Это и понятно, ведь сумма (разность, произведение, частное) обыкновенных дробей есть обыкновенная дробь (все логично, ведь рациональные числа — «разумные» числа). А как обстоит дело с иррациональными числами? Оказывается, ничего определенного сказать нельзя (что тоже логично, ведь иррациональные числа — «неразумные» числа). Смотрите: 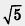 — иррациональное число, — иррациональное число, 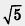 . . 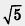 =5 — рациональное число, т. е. произведение двух иррациональных чисел оказалось рациональным числом; =5 — рациональное число, т. е. произведение двух иррациональных чисел оказалось рациональным числом;
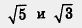 — иррациональные числа, и их произведение, т. е. — иррациональные числа, и их произведение, т. е. 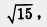 — тоже иррациональное число. То же относится к сложению, вычитанию, делению иррациональных чисел: в ответе может получиться как рациональное, так и иррациональное число. — тоже иррациональное число. То же относится к сложению, вычитанию, делению иррациональных чисел: в ответе может получиться как рациональное, так и иррациональное число.
А что получится, если в операции участвуют одно рациональное число и одно иррациональное число, какое «пересилит»?
Оказывается, «пересилит» иррациональное число. Рассмотрим такой пример: дано рациональное число 3 и иррациональное число 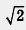 ;составим их сумму 3 + ;составим их сумму 3 + 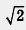 • Предположим, что это — рациональное число r, т. е. 3 + • Предположим, что это — рациональное число r, т. е. 3 + 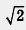 = г. Тогда = г. Тогда 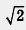 = г - 3, а r - 3 — рациональное число (как разность двух рациональных чисел). Получается, что = г - 3, а r - 3 — рациональное число (как разность двух рациональных чисел). Получается, что 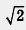 — рациональное число, а это неверно, ведь мы знаем, что это число — иррациональное. — рациональное число, а это неверно, ведь мы знаем, что это число — иррациональное.
Получили противоречие, значит, сделанное нами предположение неверно, т. е. 3 + 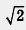 — иррациональное число. Аналогично можно доказать, что 3- — иррациональное число. Аналогично можно доказать, что 3-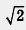 — иррациональное число. — иррациональное число.
Замечание. Обратите внимание, что в проведенном рассуждении мы снова использовали метод доказательства от противного, о котором в первый раз говорили выше, в § 15.
Итак, можно сделать следующие выводы:
• Любая арифметическая операция над рациональными числами (кроме деления на 0) приводит в результате к рациональному числу.
• Арифметическая операция над иррациональными числами может привести в результате как к рациональному, так и к иррациональному числу.
• Если в арифметической операции участвуют рациональное и иррациональное числа, то в результате получится иррациональное число (кроме умножения и деления на 0).
Поскольку операция извлечения квадратного корня из положительного числа часто приводит к иррациональным числам, условились алгебраическое выражение, в котором присутствует операция извлечения квадратного корня, называть иррациональным выражением.
Кстати, и термин «освобождение от иррациональности в знаменателе», который мы использовали в § 18, объясняется теми же причинами.
Мордкович А. Г., Алгебра. 8 кл.: Учеб. для общеобразоват. учреждений.— 3-е изд., доработ. — М.: Мнемозина, 2001. — 223 с: ил.
Школьная библиотека онлайн, учебники и книги по всему предметам, Математика 8 класс скачать
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|










