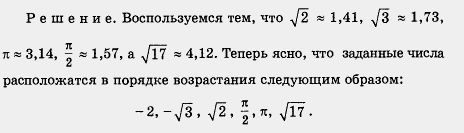|
|
|
| Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Множество действительных чисел</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Множество действительных чисел, рациональных чисел, десятичные дроби, координатной прямой, координату, квадрата, отрицательного числа, больше или, десятичных дробей</metakeywords> |
| | | | |
| - | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика:Множество действительных чисел''' | + | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика:Множество действительных чисел'''<br> |
| | | | |
| | <br> | | <br> |
| | | | |
| | + | '''Множество действительных чисел'''<br> |
| | | | |
| | + | <br>Если множество '''[[Конспект уроку на тему «Координатна пряма. Раціональні числа»|рациональных чисел]]''' дополнить множеством иррациональных чисел, то вместе они составят множество действительных чисел. Множество действительных чисел обычно обозначают буквой R; используют также символическую запись (-оо, +оо) или (-оо, оо). |
| | | | |
| - | ''' МНОЖЕСТВО ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ '''<br> | + | Множество действительных чисел можно описать так: это множество конечных и бесконечных десятичных дробей; конечные '''[[Задачі до уроку «Порівняння десяткових дробів.»|десятичные дроби]]''' и бесконечные десятичные периодические дроби — рациональные числа, а бесконечные десятичные непериодические дроби — иррациональные числа. <br> |
| | | | |
| - | <br>Если множество рациональных чисел дополнить множеством иррациональных чисел, то вместе они составят множество действительных чисел. Множество действительных чисел обычно обозначают буквой R; используют также символическую запись (-оо, +оо) или (-оо, оо).
| + | Каждое действительное число можно изобразить точкой на '''[[Порівняння натуральних чисел за допомогою координатного променя. Презентація уроку|координатной прямой]]'''. Верно и обратное: каждая точка координатной прямой имеет действительную координату. Математики обычно, говорят так: между множеством R действительных чисел и множеством точек координатной прямой установлено взаимно однозначное со ответствие. Координатная прямая есть геометрическая модель множества действительных чисел; по этой причине для координатной прямой часто используют термин числовая прямая. <br> |
| | | | |
| - | Множество действительных чисел можно описать так: это множество конечных и бесконечных десятичных дробей; конечные десятичные дроби и бесконечные десятичные периодические дроби — рациональные числа, а бесконечные десятичные непериодические дроби — иррациональные числа. <br>
| + | Вдумайтесь в этот термин: не кажется ли он вам противоестественным? Ведь число — объект алгебры, а прямая — объект геометрии. Нет ли тут «смешения жанров»? Нет, все логично, все продумано. Этот термин в очередной раз подчеркивает единство различных областей математики, дает возможность отождествления понятий «действительное число» и «точка на координатной (числовой) прямой». |
| | | | |
| - | Каждое действительное число можно изобразить точкой на координатной прямой. Верно и обратное: каждая точка координатной прямой имеет действительную координату. Математики обычно, говорят так: между множеством R действительных чисел и множеством точек координатной прямой установлено взаимно однозначное со ответствие. Координатная прямая есть геометрическая модель множества действительных чисел; по этой причине для координатной прямой часто используют термин числовая прямая. <br>
| + | Обратите внимание: координатной прямой вы пользовались начиная с 5-го класса. Но, оказывается, в ваших знаниях был вполне оправданный пробел: не для любой точки координатной прямой вы сумели бы найти '''[[Шкалы и координаты|координату]]''' — просто учитель оберегал вас от такой неприятности. <br> |
| | | | |
| - | Вдумайтесь в этот термин: не кажется ли он вам противоестественным? Ведь число — объект алгебры, а прямая — объект геометрии. Нет ли тут «смешения жанров»? Нет, все логично, все продумано. Этот термин в очередной раз подчеркивает единство различных областей математики, дает возможность <br>отождествления понятий «действительное число» и «точка на координатной (числовой) прямой».
| + | [[Image:14-06-119.jpg|240px|Задание]]<br> |
| | | | |
| - | Обратите внимание: координатной прямой вы пользовались начиная с 5-го класса. Но, оказывается, в ваших знаниях был вполне оправданный пробел: не для любой точки координатной прямой вы сумели бы найти координату — просто учитель оберегал вас от такой неприятности. <br>
| + | Рассмотрим пример. Дана координатная прямая, на ее единичном отрезке построен квадрат (рис. 100), диагональ квадрата ОВ отложена на координатной прямой от точки О вправо, получилась точка D. Чему равна координата точки D? Она равна длине диагонали '''[[Прямокутник, квадрат, їх периметри. Презентація уроку|квадрата]]''', т. е. [[Image:14-06-118.jpg]] . Это число, как мы теперь знаем, не целое и не дробь. Значит, ни в 5-м, ни в 6-м, ни в 7-м классе координату точки D вы бы найти не смогли. |
| | | | |
| - | <br> | + | Потому мы до сих пор и говорили «координатная прямая», а не «числовая прямая». <br> |
| | | | |
| - | [[Image:14-06-119.jpg]]<br>
| + | Заметим, что был еще один оправданный пробел в ваших знаниях по алгебре. Рассматривая выражения с переменными, мы всегда подразумевали, что переменные могут принимать любые допустимые значения, но только рациональные, ведь других-то не было. На самом деле переменные могут принимать любые допустимые действительные значения. Например, в тождестве (а + Ь){а-b) = а<sup>2</sup>-b<sup>2</sup> в роли а и b могут выступать любые числа, не обязательно рациональные. Этим мы уже пользовались в конце предыдущего параграфа. Этим же мы пользовались и в § 18 — в частности, в примерах 6, 7, 8 из указанного параграфа. |
| | | | |
| - | Рассмотрим пример. Дана координатная прямая, на ее единичном отрезке построен квадрат (рис. 100), диагональ квадрата ОВ отложена на координатной прямой от точки О вправо, получилась точка D. Чему равна координата точки D? Она равна длине диагонали квадрата, т. е. [[Image:14-06-118.jpg]] . Это число, как <br>мы теперь знаем, не целое и не дробь. Значит, ни в 5-м, ни в 6-м, ни в 7-м классе координату точки D вы бы найти не смогли.
| + | Для действительных чисел а, b, с выполняются привычные [http://xvatit.com/busines/strahovanie-zakon/ '''законы''']: |
| | | | |
| - | Потому мы до сих пор и говорили «координатная прямая», а не «числовая прямая». <br>
| + | а + b = b + а; |
| | | | |
| - | Заметим, что был еще один оправданный пробел в ваших знаниях по алгебре. Рассматривая выражения с переменными, мы всегда подразумевали, что переменные могут принимать любые допустимые значения, но только рациональные, ведь других-то не было. На самом деле переменные могут принимать <br>любые допустимые действительные значения. Например, в тождестве <br>(а + Ь){а-b) = а<sup>2</sup>-b<sup>2</sup> в роли а и b могут выступать любые числа, не обязательно <br>рациональные. Этим мы уже пользовались в конце предыдущего параграфа. Этим же мы пользовались и в § 18 — в частности, в примерах 6, 7, 8 из указанного параграфа.
| + | аЬ = bа; |
| | | | |
| - | Для действительных чисел а, b, с выполняются привычные законы: <br>а + b = b + а; <br>аЬ = bа;
| + | a + (b + c) = (a + b) + c<br> |
| | | | |
| - | a + (b + c) = (a + b) + c<br> | + | a(bc) =(ab)c |
| | | | |
| - | a(bc) =(ab)c<br>(а + b) с = ас + bc и т. д. <br>Выполняются и привычные правила: произведение (частное) двух положительных чисел — положительное число; <br>произведение (частное) двух отрицательных чисел — положительное число; <br>произведение (частное) положительного и отрицательного числа — отрицательное число. <br>
| + | (а + b) с = ас + bc и т. д. |
| | | | |
| - | Действительные числа можно сравнивать друг с другом, используя следующее определение. <br>
| + | Выполняются и привычные правила: произведение (частное) двух положительных чисел — положительное число; <br>произведение (частное) двух отрицательных чисел — положительное число; произведение (частное) положительного и '''[[Презентація уроку на тему «Додатні та від'ємні числа. Число 0»|отрицательного числа]]''' — отрицательное число. <br> |
| | | | |
| - | '''''Определение'''''. Говорят, что действительное число а больше (меньше) действительного числа b, если их разность а - b — положительное (отрицательное) число. Пишут а > b (а < b). <br>
| + | Действительные числа можно сравнивать друг с другом, используя следующее определение. <br> |
| | | | |
| - | Из этого определения следует, что всякое положительное число а больше нуля (поскольку разность а - 0 = а — положительное число), а всякое отрицательное число b меньше нуля (поскольку разность b - 0 = b — отрицательное число). <br>
| + | '''''Определение'''''. Говорят, что действительное число а больше (меньше) действительного числа b, если их разность а - b — положительное (отрицательное) число. Пишут а > b (а < b). <br> |
| | | | |
| - | Итак, а > 0 означает, что а — положительное число; <br>а < 0 означает, что а — отрицательное число; <br>а>b означает, что а -b — положительное число, т. е. а - b > 0; <br>a<b означает, что а - b — отрицательное число, <br>т.е. а - b < 0. <br>Наряду со знаками строгих неравенств (<, >) используют знаки нестрогих неравенств: <br>а [[Image:14-06-120.jpg]] 0 означает, что а больше нуля или равно нулю, т. е. а — неотрицательное число (положительное или 0), или что а не меньше нуля; <br>а [[Image:14-06-121.jpg]] 0 означает, что а меньше нуля или равно нулю, т. е. а — неположительное число (отрицательное или 0), или что а не больше нуля; <br>а[[Image:14-06-120.jpg]] b означает, что а больше или равно b, т. е. а - b — неотрицательное число, или что а не меньше b; а - b [[Image:14-06-120.jpg]] 0; <br>а [[Image:14-06-121.jpg]] b означает, что а меньше или равно b, т. е. а - b — неположительное число, или что а не больше Ь; а - b [[Image:14-06-121.jpg]] 0. <br>Например, для любого числа а верно неравенство а<sup>2</sup> [[Image:14-06-120.jpg]] 0; <br>для любых чисел а и b верно неравенство (а - b)<sup>2</sup> [[Image:14-06-120.jpg]] 0. <br>Впрочем, для сравнения действительных чисел необязательно каждый раз составлять их разность и выяснять, положительна она или отрицательна. Можно сделать соответствующий вывод, сравнивая записи чисел в виде десятичных дробей. | + | Из этого определения следует, что всякое положительное число а больше нуля (поскольку разность а - 0 = а — положительное число), а всякое отрицательное число b меньше нуля (поскольку разность b - 0 = b — отрицательное число). <br> |
| | + | |
| | + | Итак, а > 0 означает, что а — положительное число; |
| | + | |
| | + | а < 0 означает, что а — отрицательное число; <br>а>b означает, что а -b — положительное число, т. е. а - b > 0; <br>a<b означает, что а - b — отрицательное число, <br>т.е. а - b < 0. |
| | + | |
| | + | Наряду со знаками строгих неравенств (<, >) используют знаки нестрогих неравенств: |
| | + | |
| | + | а [[Image:14-06-120.jpg]] 0 означает, что а больше нуля или равно нулю, т. е. а — неотрицательное число (положительное или 0), или что а не меньше нуля; |
| | + | |
| | + | а [[Image:14-06-121.jpg]] 0 означает, что а меньше нуля или равно нулю, т. е. а — неположительное число (отрицательное или 0), или что а не больше нуля; |
| | + | |
| | + | а[[Image:14-06-120.jpg]] b означает, что а '''[[Меньше или больше|больше или]]''' равно b, т. е. а - b — неотрицательное число, или что а не меньше b; а - b [[Image:14-06-120.jpg]] 0; |
| | + | |
| | + | а [[Image:14-06-121.jpg]] b означает, что а меньше или равно b, т. е. а - b — неположительное число, или что а не больше Ь; а - b [[Image:14-06-121.jpg]] 0. <br>Например, для любого числа а верно неравенство а<sup>2</sup> [[Image:14-06-120.jpg]] 0; |
| | + | |
| | + | для любых чисел а и b верно неравенство (а - b)<sup>2</sup> [[Image:14-06-120.jpg]] 0. <br>Впрочем, для сравнения действительных чисел необязательно каждый раз составлять их разность и выяснять, положительна она или отрицательна. Можно сделать соответствующий вывод, сравнивая записи чисел в виде '''[[Задачі до уроку «Порівняння десяткових дробів.»|десятичных дробей]]'''. |
| | | | |
| | Геометрическая модель множества действительных чисел, т. е. числовая прямая, делает операцию сравнения чисел особенно наглядной: из двух чисел а, b больше то, которое располагается на числовой прямой правее. | | Геометрическая модель множества действительных чисел, т. е. числовая прямая, делает операцию сравнения чисел особенно наглядной: из двух чисел а, b больше то, которое располагается на числовой прямой правее. |
| Строка 49: |
Строка 67: |
| | '''Пример 1.''' Сравнить числа: | | '''Пример 1.''' Сравнить числа: |
| | | | |
| - | [[Image:14-06-122.jpg]]<br><br>'''Пример 2.''' Расположить в порядке возрастания числа | + | [[Image:14-06-122.jpg|480px|Задание]]<br><br>'''Пример 2.''' Расположить в порядке возрастания числа |
| | | | |
| - | [[Image:14-06-123.jpg]] | + | [[Image:14-06-123.jpg|180px|Задание]] |
| | | | |
| - | [[Image:14-06-124.jpg]]<br><br><br><br> | + | [[Image:14-06-124.jpg|480px|Решение]]<br>''<br>Мордкович А. Г., Алгебра. 8 кл.: Учеб. для общеобразоват. учреждений.— 3-е изд., доработ. — М.: Мнемозина, 2001. — 223 с: ил. ''<br> |
| | | | |
| - | <br> | + | <br> |
| | | | |
| | <sub>Планирование математике, материалы по математике 8 класса [[Математика|скачать]], учебники [[Гипермаркет знаний - первый в мире!|онлайн]] </sub> | | <sub>Планирование математике, материалы по математике 8 класса [[Математика|скачать]], учебники [[Гипермаркет знаний - первый в мире!|онлайн]] </sub> |
| Строка 62: |
Строка 80: |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | '''<u></u>''' | | '''<u></u>''' |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Текущая версия на 14:43, 8 октября 2012
Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика:Множество действительных чисел
Множество действительных чисел
Если множество рациональных чисел дополнить множеством иррациональных чисел, то вместе они составят множество действительных чисел. Множество действительных чисел обычно обозначают буквой R; используют также символическую запись (-оо, +оо) или (-оо, оо).
Множество действительных чисел можно описать так: это множество конечных и бесконечных десятичных дробей; конечные десятичные дроби и бесконечные десятичные периодические дроби — рациональные числа, а бесконечные десятичные непериодические дроби — иррациональные числа.
Каждое действительное число можно изобразить точкой на координатной прямой. Верно и обратное: каждая точка координатной прямой имеет действительную координату. Математики обычно, говорят так: между множеством R действительных чисел и множеством точек координатной прямой установлено взаимно однозначное со ответствие. Координатная прямая есть геометрическая модель множества действительных чисел; по этой причине для координатной прямой часто используют термин числовая прямая.
Вдумайтесь в этот термин: не кажется ли он вам противоестественным? Ведь число — объект алгебры, а прямая — объект геометрии. Нет ли тут «смешения жанров»? Нет, все логично, все продумано. Этот термин в очередной раз подчеркивает единство различных областей математики, дает возможность отождествления понятий «действительное число» и «точка на координатной (числовой) прямой».
Обратите внимание: координатной прямой вы пользовались начиная с 5-го класса. Но, оказывается, в ваших знаниях был вполне оправданный пробел: не для любой точки координатной прямой вы сумели бы найти координату — просто учитель оберегал вас от такой неприятности.
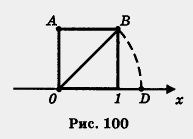
Рассмотрим пример. Дана координатная прямая, на ее единичном отрезке построен квадрат (рис. 100), диагональ квадрата ОВ отложена на координатной прямой от точки О вправо, получилась точка D. Чему равна координата точки D? Она равна длине диагонали квадрата, т. е. 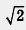 . Это число, как мы теперь знаем, не целое и не дробь. Значит, ни в 5-м, ни в 6-м, ни в 7-м классе координату точки D вы бы найти не смогли. . Это число, как мы теперь знаем, не целое и не дробь. Значит, ни в 5-м, ни в 6-м, ни в 7-м классе координату точки D вы бы найти не смогли.
Потому мы до сих пор и говорили «координатная прямая», а не «числовая прямая».
Заметим, что был еще один оправданный пробел в ваших знаниях по алгебре. Рассматривая выражения с переменными, мы всегда подразумевали, что переменные могут принимать любые допустимые значения, но только рациональные, ведь других-то не было. На самом деле переменные могут принимать любые допустимые действительные значения. Например, в тождестве (а + Ь){а-b) = а2-b2 в роли а и b могут выступать любые числа, не обязательно рациональные. Этим мы уже пользовались в конце предыдущего параграфа. Этим же мы пользовались и в § 18 — в частности, в примерах 6, 7, 8 из указанного параграфа.
Для действительных чисел а, b, с выполняются привычные законы:
а + b = b + а;
аЬ = bа;
a + (b + c) = (a + b) + c
a(bc) =(ab)c
(а + b) с = ас + bc и т. д.
Выполняются и привычные правила: произведение (частное) двух положительных чисел — положительное число;
произведение (частное) двух отрицательных чисел — положительное число; произведение (частное) положительного и отрицательного числа — отрицательное число.
Действительные числа можно сравнивать друг с другом, используя следующее определение.
Определение. Говорят, что действительное число а больше (меньше) действительного числа b, если их разность а - b — положительное (отрицательное) число. Пишут а > b (а < b).
Из этого определения следует, что всякое положительное число а больше нуля (поскольку разность а - 0 = а — положительное число), а всякое отрицательное число b меньше нуля (поскольку разность b - 0 = b — отрицательное число).
Итак, а > 0 означает, что а — положительное число;
а < 0 означает, что а — отрицательное число;
а>b означает, что а -b — положительное число, т. е. а - b > 0;
a<b означает, что а - b — отрицательное число,
т.е. а - b < 0.
Наряду со знаками строгих неравенств (<, >) используют знаки нестрогих неравенств:
а 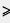 0 означает, что а больше нуля или равно нулю, т. е. а — неотрицательное число (положительное или 0), или что а не меньше нуля; 0 означает, что а больше нуля или равно нулю, т. е. а — неотрицательное число (положительное или 0), или что а не меньше нуля;
а 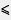 0 означает, что а меньше нуля или равно нулю, т. е. а — неположительное число (отрицательное или 0), или что а не больше нуля; 0 означает, что а меньше нуля или равно нулю, т. е. а — неположительное число (отрицательное или 0), или что а не больше нуля;
а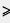 b означает, что а больше или равно b, т. е. а - b — неотрицательное число, или что а не меньше b; а - b b означает, что а больше или равно b, т. е. а - b — неотрицательное число, или что а не меньше b; а - b 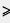 0; 0;
а 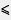 b означает, что а меньше или равно b, т. е. а - b — неположительное число, или что а не больше Ь; а - b b означает, что а меньше или равно b, т. е. а - b — неположительное число, или что а не больше Ь; а - b 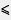 0. 0.
Например, для любого числа а верно неравенство а2 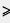 0; 0;
для любых чисел а и b верно неравенство (а - b)2 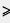 0. 0.
Впрочем, для сравнения действительных чисел необязательно каждый раз составлять их разность и выяснять, положительна она или отрицательна. Можно сделать соответствующий вывод, сравнивая записи чисел в виде десятичных дробей.
Геометрическая модель множества действительных чисел, т. е. числовая прямая, делает операцию сравнения чисел особенно наглядной: из двух чисел а, b больше то, которое располагается на числовой прямой правее.
Таким образом, к сравнению действительных чисел нужно подходить достаточно гибко, что мы и используем в следующем примере.
Пример 1. Сравнить числа:

Пример 2. Расположить в порядке возрастания числа
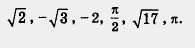
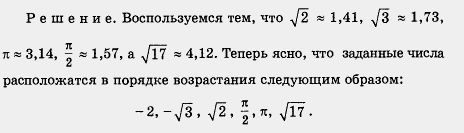
Мордкович А. Г., Алгебра. 8 кл.: Учеб. для общеобразоват. учреждений.— 3-е изд., доработ. — М.: Мнемозина, 2001. — 223 с: ил.
Планирование математике, материалы по математике 8 класса скачать, учебники онлайн
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|