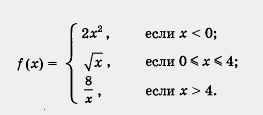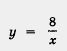|
|
|
| Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Исследование функций на монотонность</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Исследование функций на монотонность, функций, графике, неравенство, числовой прямой, линейной, луче, положительные числа, график функции</metakeywords> |
| | | | |
| - | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика:Исследование функций на монотонность''' | + | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика:Исследование функций на монотонность'''<br> |
| | | | |
| - | <br>
| |
| | | | |
| | | | |
| | + | '''Исследование функций на монотонность'''<br> |
| | | | |
| - | ''' ИССЛЕДОВАНИЕ ФУНКЦИЙ НА МОНОТОННОСТЬ '''<br> | + | <br>С понятиями возрастающей и убывающей '''[[Функция у = х2 и ее график|функций]]''' мы впервые познакомились в курсе алгебры 7-го класса. Глядя на график функции, мы снимали соответствующую информацию: если двигаясь по графику слева направо мы в то же время движемся снизу вверх (как бы поднимаемся в горку), то мы объявляли функцию возрастающей (рис. 124); если же мы движемся сверху вниз (спускаемся с горки), то мы объявляли функцию убывающей (рис. 125). <br> |
| | | | |
| - | <br>С понятиями возрастающей и убывающей функций мы впервые познакомились в курсе алгебры 7-го класса. Глядя на график функции, мы снимали соответствующую информацию: если двигаясь по графику слева направо мы в то же время движемся снизу вверх (как бы поднимаемся в горку), то мы объявляли функцию возрастающей (рис. 124); если же мы движемся сверху вниз (спускаемся с горки), то мы объявляли функцию убывающей (рис. 125). <br> | + | [[Image:15-06-16.jpg|480px|Функции]]<br>Однако математики не очень жалуют такой способ исследования свойств функции. Они считают, что определения понятий не должны опираться на рисунок, — чертеж должен лишь иллюстрировать то или иное свойство функции на ее '''[[Приклади графіків залежностей між величинами|графике]]'''. Дадим строгие определения понятий возрастания и убывания функции. <br> |
| | | | |
| - | <br> | + | '''''Определение 1.'''''Функцию у = f(x) называют возрастающей на промежутке X, если из неравенства х<sub>1</sub> < х<sub>2</sub>- где хг и х2 — любые две точки промежутка X, следует неравенство f(x<sub>1</sub>) < f(x<sub>2</sub>). <br> |
| | | | |
| - | [[Image:15-06-16.jpg]]<br><br>Однако математики не очень жалуют такой способ исследования свойств функции. Они считают, что определения понятий не должны опираться на рисунок, — чертеж должен лишь иллюстрировать то или ин е свойство функции на ее графике. Дадим строгие определения понятий возрастания и убывания функции. <br> | + | '''''Определение 2.''''' Функцию у = f(x) называют убывающей на промежутке X, если из неравенства х<sub>1</sub> < х<sub>2</sub>, где х<sub>1</sub> и х<sub>2</sub> — любые две точки промежутка X, следует '''[[Презентація до теми Розв'язування лінійних нерівностей|неравенство]]''' f(x<sub>1</sub>) > f(x<sub>2</sub>). |
| | | | |
| - | '''''Определение 1.'''''Функцию у = f(x) называют возрастающей на промежутке X, если из неравенства х<sub>1</sub> < х<sub>2</sub>- где хг и х2 — любые две точки промежутка X, следует неравенство f(x<sub>1</sub>) < f(x<sub>2</sub>). <br>
| + | На практике удобнее пользоваться следующими формулировками: |
| | | | |
| - | '''''Определение 2.''''' Функцию у = f(x) называют убывающей на промежутке X, если из неравенства х<sub>1</sub> < х<sub>2</sub>, где х<sub>1</sub> и х<sub>2</sub> — любые две точки прс лежутка X, следует неравенство f(x<sub>1</sub>) > f(x<sub>2</sub>). <br>На практике удобнее пользоваться следующими формулировками: <br>'''''функция возрастает, если большему значению аргумента соответствует большее значение функции; <br>функция убывает, если большему значению аргумента соответствует меньшее значение функции.'''''<br>
| + | функция возрастает, если большему значению аргумента соответствует большее значение функции; <br>функция убывает, если большему значению аргумента соответствует меньшее значение функции.<br> |
| | | | |
| - | Используя эти определения и установленные в § 33 свойства числовых неравенств, мы сможем обосновать выводы о возрастании или убывании ранее изученных функций. <br> | + | Используя эти определения и установленные в § 33 свойства числовых неравенств, мы сможем обосновать выводы о возрастании или убывании ранее изученных функций. <br> |
| | | | |
| - | ''' 1. Линейная функция у = kx +m '''<br>
| |
| | | | |
| - | <br>Если k > О, то функция возрастает на всей числовой прямой (рис. 126); если k < 0, то функция убывает на всей числовой прямой (рис. 127). <br>
| |
| | | | |
| - | Доказательство. Положим f(х) = kx +m. Если х<sub>1</sub> < х<sub>2</sub> и k > О, то, согласно свойству 3 числовых неравенств (см. § 33), kx<sub>1</sub> < kx<sub>2</sub>. Далее, согласно свойству 2, из kx<sub>1</sub> < kx<sub>2</sub> <br>следует, что kx<sub>1</sub> + m < kx<sub>2</sub> + m, т. е. f(х<sub>1</sub>) < f(х<sub>2</sub>). <br>
| + | <u>'''1. Линейная функция у = kx +m'''</u> |
| | | | |
| - | <br> | + | Если k > 0, то функция возрастает на всей '''[[Задачі на тему «Координатна пряма. Раціональні числа»|числовой прямой]]''' (рис. 126); если k < 0, то функция убывает на всей числовой прямой (рис. 127). <br> |
| | | | |
| - | [[Image:15-06-17.jpg]]<br><br>Итак, из неравенства х<sub>1</sub> < х<sub>2</sub> следует, что f(х<sub>1</sub>) < f(x<sub>2</sub>). Это и означает возрастание функции у = f(х), т.е. линейной функции у = kx+ m. <br>Если же х<sub>1</sub> < х<sub>2</sub> и k < 0, то, согласно свойству 3 числовых неравенств, kx<sub>1</sub> > kx<sub>2</sub>, а согласно свойству 2, из kx<sub>1</sub> > kx<sub>2</sub> следует, что kx<sub>1</sub> + m> kx<sub>2</sub> + т.<br>
| + | Доказательство. Положим f(х) = kx +m. Если х<sub>1</sub> < х<sub>2</sub> и k > О, то, согласно свойству 3 числовых неравенств (см. § 33), kx<sub>1</sub> < kx<sub>2</sub>. Далее, согласно свойству 2, из kx<sub>1</sub> < kx<sub>2</sub> следует, что kx<sub>1</sub> + m < kx<sub>2</sub> + m, т. е. f(х<sub>1</sub>) < f(х<sub>2</sub>). <br> |
| | | | |
| - | Итак, из неравенства х<sub>1</sub> < х<sub>2</sub> следует, что f(х<sub>1</sub>) > f(х<sub>2</sub>). Это и означает убывание функции у = f(x), т. е. линейной функции у = kx + m. <br> | + | [[Image:15-06-17.jpg|480px|Линейная функция]]<br><br>Итак, из неравенства х<sub>1</sub> < х<sub>2</sub> следует, что f(х<sub>1</sub>) < f(x<sub>2</sub>). Это и означает возрастание функции у = f(х), т.е. '''[[Розв'язування системи лінійних рівнянь з двома змінними способом додавання|линейной]]''' функции у = kx+ m. |
| | | | |
| - | Если функция возрастает (убывает) во всей своей области определения, то ее можно называть возрастающей (убывающей), не указывая промежутка. Например, про функцию у = 2х - 3 можно сказать, что она возрастает на всей числовой прямой, но можно сказать и короче: у = 2х - 3 — возрастающая <br>функция. <br> | + | Если же х<sub>1</sub> < х<sub>2</sub> и k < 0, то, согласно свойству 3 числовых неравенств, kx<sub>1</sub> > kx<sub>2</sub>, а согласно свойству 2, из kx<sub>1</sub> > kx<sub>2</sub> следует, что kx<sub>1</sub> + m> kx<sub>2</sub> + т.<br> |
| | | | |
| - | <br>''' 2. Функция у = х2 '''<br> | + | Итак, из неравенства х<sub>1</sub> < х<sub>2</sub> следует, что f(х<sub>1</sub>) > f(х<sub>2</sub>). Это и означает убывание функции у = f(x), т. е. линейной функции у = kx + m. <br> |
| | | | |
| - | <br>1. Рассмотрим функцию у = х<sup>2</sup> на луче [0, + <sub>00</sub>). Пусть 0 [[Image:15-06-18.jpg]] х<sub>1</sub> < х<sub>2</sub>. Тогда, согласно свойству 6 числовых неравенств, [[Image:15-06-19.jpg]], т. е.f(x<sub>1</sub>) < f(x<sub>2</sub>)- Итак, из х<sub>1</sub> < х<sub>2</sub> следует f(x<sub>1</sub>) < f(x<sub>2</sub>). Таким образом, функция у = х<sup>2</sup> возрастает на луче [0, + <sub>00</sub>) (рис. 128). <br>
| + | Если функция возрастает (убывает) во всей своей области определения, то ее можно называть возрастающей (убывающей), не указывая промежутка. Например, про функцию у = 2х - 3 можно сказать, что она возрастает на всей числовой прямой, но можно сказать и короче: у = 2х - 3 — возрастающая <br>функция. <br> |
| | | | |
| - | [[Image:15-06-20.jpg]]<br>
| + | <br><u>'''2. Функция у = х2'''</u> |
| | | | |
| - | 2. Рассмотрим функцию у = х<sup>2</sup> на луче (- со, 0]. Возьмем два неположительных числа х<sub>1</sub> и х<sub>2</sub>, таких, что х<sub>1</sub> < х<sub>2</sub>. Тогда, согласно свойству 3 числовых <br>неравенств, выполняется неравенство - х<sub>1</sub> > - х<sub>2</sub>. Так как числа - х<sub>1</sub> и - х<sub>2</sub> неотрицательны, то, возведя в квадрат обе части последнего неравенства, получим неравенство того же смысла (-х<sub>1</sub>)<sup>2</sup> > (-х<sub>2</sub>)<sup>2</sup>, т.е. [[Image:15-06-21.jpg]] Это значит, что f(х<sub>1</sub>) >f(х<sub>2</sub>). <br>Итак, из неравенства х<sub>1</sub> < х<sub>2</sub> следует, что f(х<sub>1</sub>) > f(х<sub>2</sub>). <br>Поэтому функция у = х<sup>2</sup> убывает на луче (- <sub>00</sub>, 0] (рис. 128). <br><br>3. Функция у [[Image:15-06-22.jpg]]<br><br>1. Рассмотрим функцию [[Image:15-06-22.jpg]] на промежутке (0, + <sub>00</sub>). <br>Пусть х1 < х<sub>2</sub>. Так как х<sub>1</sub> и х<sub>2</sub> — положительные числа, то из х<sub>1</sub>< x<sub>2</sub> следует [[Image:15-06-23.jpg]] (см. пример 1 из § 33), т. е. f(x<sub>1</sub>) > f(x<sub>2</sub>). <br>Итак, из неравенства х<sub>1</sub> < х<sub>2</sub> следует, что f(x<sub>1</sub>) > f(x<sub>2</sub>). Это значит, что функция убывает на открытом луче (0, + <sub>00</sub>) (рис. 129). <br>
| + | 1. Рассмотрим функцию у = х<sup>2</sup> на луче [0, + <sub>00</sub>). Пусть 0 [[Image:15-06-18.jpg]] х<sub>1</sub> < х<sub>2</sub>. Тогда, согласно свойству 6 числовых неравенств, [[Image:15-06-19.jpg]], т. е.f(x<sub>1</sub>) < f(x<sub>2</sub>)- Итак, из х<sub>1</sub> < х<sub>2</sub> следует f(x<sub>1</sub>) < f(x<sub>2</sub>). Таким образом, функция у = х<sup>2</sup> возрастает на '''[[Плоскость. Прямая. Луч|луче]]''' [0, + <sub>00</sub>) (рис. 128). <br> |
| | | | |
| - | [[Image:15-06-24.jpg]]<br>2. Рассмотрим функцию [[Image:15-06-22.jpg]] на промежутке (-оо, 0). Пусть х<sub>1</sub> < х<sub>2</sub>, х<sub>1</sub> и х<sub>2</sub> — отрицательные числа. Тогда - х<sub>1</sub> > - х<sub>2</sub>, причем обе части последнего неравен- <br>ства — положительные числа, а потому [[Image:15-06-25.jpg]] (мы снова воспользовались неравенством, доказанным в примере 1 из § 33). Далее имеем [[Image:15-06-26.jpg]][[Image:15-06-27.jpg]], откуда получаем [[Image:15-06-28.jpg]] . <br>Итак, из неравенства х<sub>1</sub> < х<sub>2</sub> следует, что f(x<sub>1</sub>) >f(x<sub>2</sub>) т.е. функция убывает на открытом луче (-<sub>00</sub>, 0) <br>Обычно термины «возрастающая функция», «убывающая функция» объединяют общим названием монотонная функция, а исследование функции на возрастание и убывание называют исследованием функции на монотонность. <br> | + | [[Image:15-06-20.jpg|240px|Функция]]<br> |
| | | | |
| - | '''Пример'''. Построить и прочитать график функции y = f{x), где <br>
| + | 2. Рассмотрим функцию у = х<sup>2</sup> на луче (- со, 0]. Возьмем два неположительных числа х<sub>1</sub> и х<sub>2</sub>, таких, что х<sub>1</sub> < х<sub>2</sub>. Тогда, согласно свойству 3 числовых неравенств, выполняется неравенство - х<sub>1</sub> > - х<sub>2</sub>. Так как числа - х<sub>1</sub> и - х<sub>2</sub> неотрицательны, то, возведя в квадрат обе части последнего неравенства, получим неравенство того же смысла (-х<sub>1</sub>)<sup>2</sup> > (-х<sub>2</sub>)<sup>2</sup>, т.е. [[Image:15-06-21.jpg]] Это значит, что f(х<sub>1</sub>) >f(х<sub>2</sub>). |
| | | | |
| - | <br> | + | Итак, из неравенства х<sub>1</sub> < х<sub>2</sub> следует, что f(х<sub>1</sub>) > f(х<sub>2</sub>). |
| | | | |
| - | [[Image:15-06-29.jpg]]<br><br>Решение.<br> | + | Поэтому функция у = х<sup>2</sup> убывает на луче (- <sub>00</sub>, 0] (рис. 128). <br>3. Функция у [[Image:15-06-22.jpg]]<br>1. Рассмотрим функцию [[Image:15-06-22.jpg]] на промежутке (0, + <sub>00</sub>). <br>Пусть х1 < х<sub>2</sub>. Так как х<sub>1</sub> и х<sub>2</sub> — '''[[Презентація уроку на тему «Додатні та від'ємні числа. Число 0»|положительные числа]]''', то из х<sub>1</sub>< x<sub>2</sub> следует [[Image:15-06-23.jpg]] (см. пример 1 из § 33), т. е. f(x<sub>1</sub>) > f(x<sub>2</sub>). |
| | | | |
| - | 1) Построим график функции у = 2х<sup>2</sup> и возьмем ветвь этой параболы при х < 0 (рис. 130). <br> | + | Итак, из неравенства х<sub>1</sub> < х<sub>2</sub> следует, что f(x<sub>1</sub>) > f(x<sub>2</sub>). Это значит, что функция убывает на открытом луче (0, + <sub>00</sub>) (рис. 129). <br> |
| | | | |
| - | 2) Построим график функции [[Image:15-06-30.jpg]] и выделим его часть на отрезке [0, 4] (рис. 131). <br> | + | [[Image:15-06-24.jpg|240px|Функция]]<br>2. Рассмотрим функцию [[Image:15-06-22.jpg]] на промежутке (-оо, 0). Пусть х<sub>1</sub> < х<sub>2</sub>, х<sub>1</sub> и х<sub>2</sub> — отрицательные числа. Тогда - х<sub>1</sub> > - х<sub>2</sub>, причем обе части последнего неравенства — положительные числа, а потому [[Image:15-06-25.jpg]] (мы снова воспользовались неравенством, доказанным в примере 1 из § 33). Далее имеем [[Image:15-06-26.jpg]][[Image:15-06-27.jpg]], откуда получаем [[Image:15-06-28.jpg]] . |
| | | | |
| - | [[Image:15-06-31.jpg]]<br>
| + | Итак, из неравенства х<sub>1</sub> < х<sub>2</sub> следует, что f(x<sub>1</sub>) >f(x<sub>2</sub>) т.е. функция убывает на открытом луче (-<sub>00</sub>, 0) |
| | | | |
| - | <br>3) Построим гиперболу [[Image:15-06-32.jpg]] и выделим ее часть на открытом луче (4, + <sub>00</sub>) (рис. 132). <br>4) Все три «кусочка» изобразим в одной системе координат — это и есть график функции у = f(x) (рис. 133). <br>Прочитаем график функции у = f(x). <br>1. Область определения функции — вся числовая прямая. <br>
| + | Обычно термины «возрастающая функция», «убывающая функция» объединяют общим названием монотонная функция, а исследование функции на возрастание и убывание называют исследованием функции на монотонность. <br> |
| | | | |
| - | 2. у = 0 при х = 0; у > 0 при х > 0. <br> | + | '''Пример'''. Построить и прочитать график функции y = f{x), где <br> |
| | + | |
| | + | [[Image:15-06-29.jpg|320px|график функции]]<br>'''<br>Решение.'''<br> |
| | + | |
| | + | 1) Построим график функции у = 2х<sup>2</sup> и возьмем ветвь этой параболы при х < 0 (рис. 130). <br> |
| | + | |
| | + | 2) Построим '''[[Функції, їх графіки та властивості|график функции]]''' [[Image:15-06-30.jpg]] и выделим его часть на отрезке [0, 4] (рис. 131). <br> |
| | + | |
| | + | [[Image:15-06-31.jpg|480px|График функции]]<br>3) Построим гиперболу [[Image:15-06-32.jpg]] и выделим ее часть на открытом луче (4, + <sub>00</sub>) (рис. 132). <br>4) Все три «кусочка» изобразим в одной системе координат — это и есть график функции у = f(x) (рис. 133). |
| | + | |
| | + | Прочитаем график функции у = f(x). |
| | + | |
| | + | 1. Область определения функции — вся числовая прямая. <br> |
| | + | |
| | + | 2. у = 0 при х = 0; у > 0 при х > 0. <br> |
| | | | |
| | 3. Функция убывает на луче (-оо, 0], возрастает на отрезке [0, 4], убывает на луче [4, + оо). | | 3. Функция убывает на луче (-оо, 0], возрастает на отрезке [0, 4], убывает на луче [4, + оо). |
| Строка 73: |
Строка 85: |
| | 8. Функция выпукла вниз на луче (-оо, 0], выпукла вверх на отрезке [0, 4], выпукла вниз на луче [4, + оо). | | 8. Функция выпукла вниз на луче (-оо, 0], выпукла вверх на отрезке [0, 4], выпукла вниз на луче [4, + оо). |
| | | | |
| - | [[Image:15-06-33.jpg]]<br><br> | + | [[Image:15-06-33.jpg|480px|график функции]] |
| | | | |
| - | <br> | + | <br>''Мордкович А. Г., [http://xvatit.com/vuzi/ '''Алгебра.'''] 8 кл.: Учеб. для общеобразоват. учреждений.— 3-е изд., доработ. — М.: Мнемозина, 2001. — 223 с: ил. ''<br> |
| | + | |
| | + | <br> |
| | | | |
| | <sub>Рефераты, домашняя работа по математике [[Математика|скачать]], учебники скатать бесплатно, [[Гипермаркет знаний - первый в мире!|онлайн]] уроки, вопросы и ответы</sub> | | <sub>Рефераты, домашняя работа по математике [[Математика|скачать]], учебники скатать бесплатно, [[Гипермаркет знаний - первый в мире!|онлайн]] уроки, вопросы и ответы</sub> |
| Строка 82: |
Строка 96: |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | '''<u></u>''' | | '''<u></u>''' |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Текущая версия на 19:26, 8 октября 2012
Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика:Исследование функций на монотонность
Исследование функций на монотонность
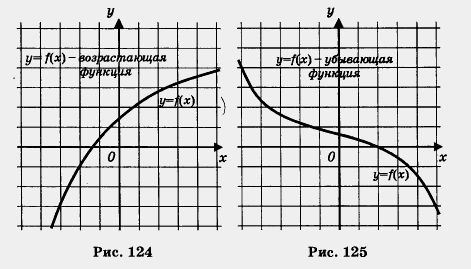
С понятиями возрастающей и убывающей функций мы впервые познакомились в курсе алгебры 7-го класса. Глядя на график функции, мы снимали соответствующую информацию: если двигаясь по графику слева направо мы в то же время движемся снизу вверх (как бы поднимаемся в горку), то мы объявляли функцию возрастающей (рис. 124); если же мы движемся сверху вниз (спускаемся с горки), то мы объявляли функцию убывающей (рис. 125).
Однако математики не очень жалуют такой способ исследования свойств функции. Они считают, что определения понятий не должны опираться на рисунок, — чертеж должен лишь иллюстрировать то или иное свойство функции на ее графике. Дадим строгие определения понятий возрастания и убывания функции.
Определение 1.Функцию у = f(x) называют возрастающей на промежутке X, если из неравенства х1 < х2- где хг и х2 — любые две точки промежутка X, следует неравенство f(x1) < f(x2).
Определение 2. Функцию у = f(x) называют убывающей на промежутке X, если из неравенства х1 < х2, где х1 и х2 — любые две точки промежутка X, следует неравенство f(x1) > f(x2).
На практике удобнее пользоваться следующими формулировками:
функция возрастает, если большему значению аргумента соответствует большее значение функции;
функция убывает, если большему значению аргумента соответствует меньшее значение функции.
Используя эти определения и установленные в § 33 свойства числовых неравенств, мы сможем обосновать выводы о возрастании или убывании ранее изученных функций.
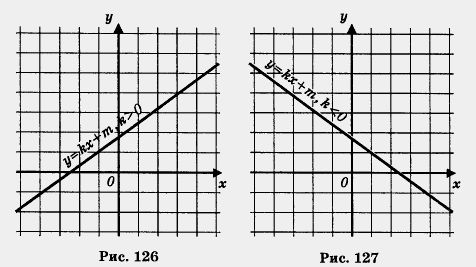
1. Линейная функция у = kx +m
Если k > 0, то функция возрастает на всей числовой прямой (рис. 126); если k < 0, то функция убывает на всей числовой прямой (рис. 127).
Доказательство. Положим f(х) = kx +m. Если х1 < х2 и k > О, то, согласно свойству 3 числовых неравенств (см. § 33), kx1 < kx2. Далее, согласно свойству 2, из kx1 < kx2 следует, что kx1 + m < kx2 + m, т. е. f(х1) < f(х2).
Итак, из неравенства х1 < х2 следует, что f(х1) < f(x2). Это и означает возрастание функции у = f(х), т.е. линейной функции у = kx+ m.
Если же х1 < х2 и k < 0, то, согласно свойству 3 числовых неравенств, kx1 > kx2, а согласно свойству 2, из kx1 > kx2 следует, что kx1 + m> kx2 + т.
Итак, из неравенства х1 < х2 следует, что f(х1) > f(х2). Это и означает убывание функции у = f(x), т. е. линейной функции у = kx + m.
Если функция возрастает (убывает) во всей своей области определения, то ее можно называть возрастающей (убывающей), не указывая промежутка. Например, про функцию у = 2х - 3 можно сказать, что она возрастает на всей числовой прямой, но можно сказать и короче: у = 2х - 3 — возрастающая
функция.
2. Функция у = х2
1. Рассмотрим функцию у = х2 на луче [0, + 00). Пусть 0 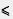 х1 < х2. Тогда, согласно свойству 6 числовых неравенств, х1 < х2. Тогда, согласно свойству 6 числовых неравенств, 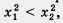 , т. е.f(x1) < f(x2)- Итак, из х1 < х2 следует f(x1) < f(x2). Таким образом, функция у = х2 возрастает на луче [0, + 00) (рис. 128). , т. е.f(x1) < f(x2)- Итак, из х1 < х2 следует f(x1) < f(x2). Таким образом, функция у = х2 возрастает на луче [0, + 00) (рис. 128).
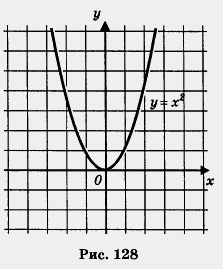
2. Рассмотрим функцию у = х2 на луче (- со, 0]. Возьмем два неположительных числа х1 и х2, таких, что х1 < х2. Тогда, согласно свойству 3 числовых неравенств, выполняется неравенство - х1 > - х2. Так как числа - х1 и - х2 неотрицательны, то, возведя в квадрат обе части последнего неравенства, получим неравенство того же смысла (-х1)2 > (-х2)2, т.е. 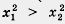 Это значит, что f(х1) >f(х2). Это значит, что f(х1) >f(х2).
Итак, из неравенства х1 < х2 следует, что f(х1) > f(х2).
Поэтому функция у = х2 убывает на луче (- 00, 0] (рис. 128).
3. Функция у 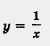
1. Рассмотрим функцию 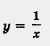 на промежутке (0, + 00). на промежутке (0, + 00).
Пусть х1 < х2. Так как х1 и х2 — положительные числа, то из х1< x2 следует 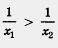 (см. пример 1 из § 33), т. е. f(x1) > f(x2). (см. пример 1 из § 33), т. е. f(x1) > f(x2).
Итак, из неравенства х1 < х2 следует, что f(x1) > f(x2). Это значит, что функция убывает на открытом луче (0, + 00) (рис. 129).
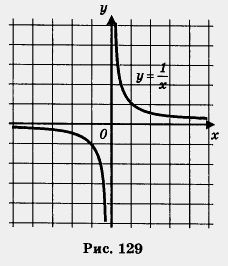
2. Рассмотрим функцию 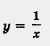 на промежутке (-оо, 0). Пусть х1 < х2, х1 и х2 — отрицательные числа. Тогда - х1 > - х2, причем обе части последнего неравенства — положительные числа, а потому на промежутке (-оо, 0). Пусть х1 < х2, х1 и х2 — отрицательные числа. Тогда - х1 > - х2, причем обе части последнего неравенства — положительные числа, а потому 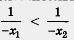 (мы снова воспользовались неравенством, доказанным в примере 1 из § 33). Далее имеем (мы снова воспользовались неравенством, доказанным в примере 1 из § 33). Далее имеем 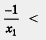 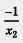 , откуда получаем , откуда получаем 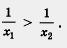 . .
Итак, из неравенства х1 < х2 следует, что f(x1) >f(x2) т.е. функция убывает на открытом луче (-00, 0)
Обычно термины «возрастающая функция», «убывающая функция» объединяют общим названием монотонная функция, а исследование функции на возрастание и убывание называют исследованием функции на монотонность.
Пример. Построить и прочитать график функции y = f{x), где
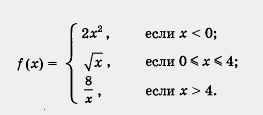
Решение.
1) Построим график функции у = 2х2 и возьмем ветвь этой параболы при х < 0 (рис. 130).
2) Построим график функции 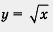 и выделим его часть на отрезке [0, 4] (рис. 131). и выделим его часть на отрезке [0, 4] (рис. 131).
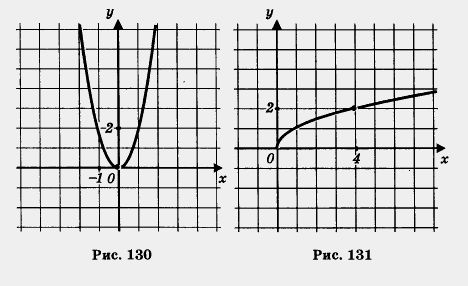
3) Построим гиперболу 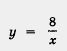 и выделим ее часть на открытом луче (4, + 00) (рис. 132). и выделим ее часть на открытом луче (4, + 00) (рис. 132).
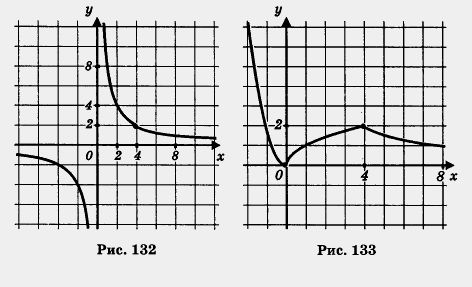
4) Все три «кусочка» изобразим в одной системе координат — это и есть график функции у = f(x) (рис. 133).
Прочитаем график функции у = f(x).
1. Область определения функции — вся числовая прямая.
2. у = 0 при х = 0; у > 0 при х > 0.
3. Функция убывает на луче (-оо, 0], возрастает на отрезке [0, 4], убывает на луче [4, + оо).
4. Функция ограничена снизу, но не ограничена сверху.
5. унаим. = 0 (достигается при х = 0); Yнаиб- не существует.
6. Функция непрерывна.
7. Область значений функции — луч [0, + оо).
8. Функция выпукла вниз на луче (-оо, 0], выпукла вверх на отрезке [0, 4], выпукла вниз на луче [4, + оо).
Мордкович А. Г., Алгебра. 8 кл.: Учеб. для общеобразоват. учреждений.— 3-е изд., доработ. — М.: Мнемозина, 2001. — 223 с: ил.
Рефераты, домашняя работа по математике скачать, учебники скатать бесплатно, онлайн уроки, вопросы и ответы
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|