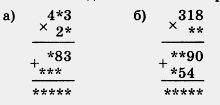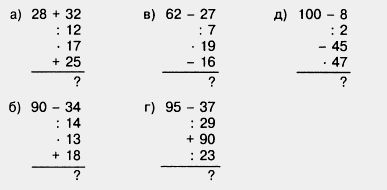|
|
|
| Строка 5: |
Строка 5: |
| | <br> | | <br> |
| | | | |
| - | ''' Умножение натуральных чисел и его свойства ''' | + | '''Умножение натуральных чисел и его свойства ''' |
| | | | |
| - | <br>Если концертный зал освещается тремя люстрами по 25 лампочек в каждой, то всего лампочек в этих люстрах будет 25 + 25 + 25, то есть 75. <br>Сумму, в которой все слагаемые равны друг другу, записывают короче: вместо 25 + 25 + 25 пишут 25 • 3. <br>Значит, 25 • 3 = 75. Число 75 называют произведением чисел 25 и 3, а числа 25 и 3 называют множителями. <br>'''Умножить''' '''число''' m на '''натуральное число''' n — значит найти '''сумму''' n слагаемых, каждое из которых равно m. <br>Выражение m • n и значение этого выражения называют '''произведением''' чисел m и n. Числа m и n называют '''множителями'''. | + | <br>Если концертный зал освещается тремя люстрами по 25 лампочек в каждой, то всего лампочек в этих люстрах будет 25 + 25 + 25, то есть 75. |
| | | | |
| - | [[Image:15-06-137.jpg]]<br><br>Произведения 7 • 4 и 4 • 7 равны одному и тому же числу 28 (рис. 46). | + | [http://xvatit.com/busines/ '''Сумму'''], в которой все слагаемые равны друг другу, записывают короче: вместо 25 + 25 + 25 пишут 25 • 3. <br>Значит, 25 • 3 = 75. Число 75 называют произведением чисел 25 и 3, а числа 25 и 3 называют множителями. |
| | | | |
| - | [[Image:15-06-138.jpg]]<br><br>1. Произведение двух чисел не изменяется при перестановке множителей. <br>Это свойство умножения называют '''переместительным'''. С помощью букв его записывают так:
| + | Умножить число m на натуральное число n — значит найти сумму n слагаемых, каждое из которых равно m. |
| | | | |
| - | а • b = b • а. <br>Произведения (5 • 3) • 2 = 15 • 2 и 5 • (3 - 2) = 5 • 6 имеют одно и то же значение 30. Значит, 5 • (3 • 2) = (5 • 3) • 2 (рис. 47).
| + | Выражение m • n и значение этого выражения называют произведением чисел m и n. Числа m и n называют множителями. |
| | | | |
| - | 2. Чтобы умножить число на произведение двух чисел, можно сначала умножить его на первый множитель, а потом полученное произведение умножить на второй множитель. <br>Это свойство умножения называют '''сочетательным'''. С помощью букв его записывают так: <br>a • (b • с) = (а • b) • с. <br>Сумма n слагаемых, каждое из которых равно 1, равна n. Поэтому верно <br>равенство 1 • n = n. <br>Сумма п слагаемых, каждое из которых равно нулю, равна нулю. Поэтому верно равенство 0 • п = 0. <br>Чтобы переместительное свойство умножения было верно при n = 1 и n = 0, условились, что m • 1 = m и m • 0 = 0. <br>Перед буквенными множителями обычно не пишут знак умножения: вмето 8 • х пишут 8х, вместо a • b пишут ab. <br>Опускают знак умножения и перед скобками. Например, вместо 2 • (а + b) пишут 2(а + b), а вместо (х + 2) • (y + 3) пишут (х + 2)(у + 3). <br>Вместо (аЬ)с пишут abc. <br>Когда в записи произведения нет скобок, умножение выполняют по порядку слева направо. <br>
| + | [[Image:15-06-137.jpg|180px|Умножение натуральных чисел]]<br><br>Произведения 7 • 4 и 4 • 7 равны одному и тому же числу 28 (рис. 46). |
| | | | |
| - | '''Что значит умножить одно натуральное число на другое? <br>Как называют числа, которые перемножают? <br>Как называют результат умножения? <br>Чему равно 1 • n? Чему равно О • n? <br>Сформулируйте переместительное свойство умножения. Запишите его а а 0 <br>с помощью букв. • 4г • <br>Сформулируйте сочетательное свойство умножения. Запишите его °$ tf 9* <br>с помощью букв. <br>В каких случаях можно опустить знак умножения? <br>Чему равно произведение m • 1 ? <br>Чему равно произведение m • 0? '''<br>
| + | [[Image:15-06-138.jpg|550px|Умножение натуральных чисел]]<br><br>1. Произведение двух чисел не изменяется при перестановке множителей. Это свойство умножения называют переместительным. С помощью букв его записывают так: |
| | | | |
| - | <br>404. Представьте в виде произведения сумму: <br>а) 707 + 707 + 707; <br>б) 50 4- 50 + 50 + 50 + 50 + 50; <br>b) x + x + x + x + x + x
| + | а • b = b • а. |
| | | | |
| - | 405. Представьте в виде суммы произведение: <br>а) 712 • 3; в) (х + у) • 4; <br>б) а • 6; г) (k + m + 4) • 2.
| + | Произведения (5 • 3) • 2 = 15 • 2 и 5 • (3 - 2) = 5 • 6 имеют одно и то же значение 30. Значит, 5 • (3 • 2) = (5 • 3) • 2 (рис. 47). |
| | + | |
| | + | 2. Чтобы умножить число на произведение двух чисел, можно сначала умножить его на первый множитель, а потом полученное произведение умножить на второй множитель. |
| | + | |
| | + | Это свойство умножения называют сочетательным. С помощью букв его записывают так: |
| | + | |
| | + | a • (b • с) = (а • b) • с. |
| | + | |
| | + | Сумма n слагаемых, каждое из которых равно 1, равна n. Поэтому верно равенство 1 • n = n. |
| | + | |
| | + | Сумма п слагаемых, каждое из которых равно нулю, равна нулю. Поэтому верно равенство 0 • п = 0. |
| | + | |
| | + | Чтобы переместительное свойство умножения было верно при n = 1 и n = 0, условились, что m • 1 = m и m • 0 = 0. |
| | + | |
| | + | Перед буквенными множителями обычно не пишут знак умножения: вмето 8 • х пишут 8х, вместо a • b пишут ab. |
| | + | |
| | + | Опускают знак умножения и перед скобками. Например, вместо 2 • (а + b) пишут 2(а + b), а вместо (х + 2) • (y + 3) пишут (х + 2)(у + 3). |
| | + | |
| | + | Вместо (аb)с пишут abc. |
| | + | |
| | + | Когда в записи произведения нет скобок, умножение выполняют по порядку слева направо. <br> |
| | + | |
| | + | ''Что значит умножить одно натуральное число на другое? <br>Как называют числа, которые перемножают? <br>Как называют результат умножения? <br>Чему равно 1 • n? Чему равно О • n? <br>Сформулируйте переместительное свойство умножения. Запишите его а а 0 с помощью букв. • 4г • <br>Сформулируйте сочетательное свойство умножения. Запишите его °$ tf 9* с помощью букв. <br>В каких случаях можно опустить знак умножения? <br>Чему равно произведение m • 1 ? <br>Чему равно произведение m • 0? ''<br> |
| | + | |
| | + | <br>404. Представьте в виде произведения сумму: |
| | + | |
| | + | а) 707 + 707 + 707; <br>б) 50 4- 50 + 50 + 50 + 50 + 50; <br>b) x + x + x + x + x + x |
| | + | |
| | + | 405. Представьте в виде суммы произведение: |
| | + | |
| | + | а) 712 • 3; в) (х + у) • 4; <br>б) а • 6; г) (k + m + 4) • 2. |
| | | | |
| | <br> | | <br> |
| | | | |
| - | [[Image:15-06-139.jpg]] | + | [[Image:15-06-139.jpg|550px|Правило]] |
| | | | |
| | <br>406. Вместо слов «представьте в виде произведения» говорят «разложите на множители». Разложите всеми способами на два множителя число 12. | | <br>406. Вместо слов «представьте в виде произведения» говорят «разложите на множители». Разложите всеми способами на два множителя число 12. |
| Строка 41: |
Строка 71: |
| | 412. Найдите значение произведения: | | 412. Найдите значение произведения: |
| | | | |
| - | [[Image:15-06-140.jpg]]<br><br>413. Найдите значение выражения: | + | [[Image:15-06-140.jpg|480px|Задание]]<br><br>413. Найдите значение выражения: |
| | | | |
| | а) 305 + 305 + 305 + 305 + 73; <br>б) 615 + 615 + 125 + 125 + 125; <br>в) 2011 + 402 + 402 + 402 + 402 + 402; <br>г) 58 + 58 + 58 + 58 + 58 + 720 + 720. <br><br>414. Вместо звездочек поставьте пропущенные цифры: | | а) 305 + 305 + 305 + 305 + 73; <br>б) 615 + 615 + 125 + 125 + 125; <br>в) 2011 + 402 + 402 + 402 + 402 + 402; <br>г) 58 + 58 + 58 + 58 + 58 + 720 + 720. <br><br>414. Вместо звездочек поставьте пропущенные цифры: |
| | | | |
| - | [[Image:15-06-141.jpg]]<br><br>415. Выполните действия, применив сочетательное свойство умножения: | + | [[Image:15-06-141.jpg|240px|Задание]]<br><br>415. Выполните действия, применив сочетательное свойство умножения: |
| | | | |
| | а) 50 • (2 • 764); в) 125 • (4 • 80); <br>б) (111 • 2) • 35; г) (402 • 125) • 8. | | а) 50 • (2 • 764); в) 125 • (4 • 80); <br>б) (111 • 2) • 35; г) (402 • 125) • 8. |
| Строка 55: |
Строка 85: |
| | 417. В магазин привезли 5 ящиков с красками. В каждом ящике 144 коробки, а в каждой коробке 12 тюбиков с красками. Сколько тюбиков привезли в магазин? Решите задачу двумя способами. | | 417. В магазин привезли 5 ящиков с красками. В каждом ящике 144 коробки, а в каждой коробке 12 тюбиков с красками. Сколько тюбиков привезли в магазин? Решите задачу двумя способами. |
| | | | |
| - | 418. Столяр и его помощник должны сделать 217 рам. Столяр в день делает 18 рам, а его помощник — 13. Сколько рам им останется сделать после двух дней, работы? четырех дней работы? семи дней работы? | + | 418. [http://xvatit.com/vuzi/ '''Столяр'''] и его помощник должны сделать 217 рам. Столяр в день делает 18 рам, а его помощник — 13. Сколько рам им останется сделать после двух дней, работы? четырех дней работы? семи дней работы? |
| | | | |
| | 419. Для покраски двери требуется 800 г белил, а для покраски окна на 200 г меньше. Сколько белил потребуется, чтобы покрасить 3 окна и 4 двери? | | 419. Для покраски двери требуется 800 г белил, а для покраски окна на 200 г меньше. Сколько белил потребуется, чтобы покрасить 3 окна и 4 двери? |
| | | | |
| - | 420. Составьте выражение для решения задачи: <br>а) Построили 5 коттеджей по 80 м2 жилой площади и 2 коттеджа по 140 м2. Какова жилая площадь всех этих коттеджей? <br>б) Масса контейнера с четырьмя книжными шкафами 3 ц. Какова масса пустого контейнера, если масса одного шкафа 58 кг? | + | 420. Составьте выражение для решения задачи: |
| | + | |
| | + | а) Построили 5 коттеджей по 80 м2 жилой площади и 2 коттеджа по 140 м2. Какова жилая площадь всех этих коттеджей? |
| | + | |
| | + | б) Масса контейнера с четырьмя книжными шкафами 3 ц. Какова масса пустого контейнера, если масса одного шкафа 58 кг? |
| | | | |
| | 421. Привезли 12 ящиков яблок, по 30 кг в каждом, и 8 ящиков груш, по 40 кг в каждом. Какой смысл имеют следующие выражения: | | 421. Привезли 12 ящиков яблок, по 30 кг в каждом, и 8 ящиков груш, по 40 кг в каждом. Какой смысл имеют следующие выражения: |
| Строка 79: |
Строка 113: |
| | а) произведение m и n; <br>б) утроенная сумма а и b; <br>в) сумма произведений чисел 6 и х и чисел 8 и у; <br>г) произведение разности чисел а и b и числа с. | | а) произведение m и n; <br>б) утроенная сумма а и b; <br>в) сумма произведений чисел 6 и х и чисел 8 и у; <br>г) произведение разности чисел а и b и числа с. |
| | | | |
| - | 426. Прочитайте выражение: <br>а) а • (с + d); в) 3(m+ n); д) аb + с; <br>б) (4 - а) • 8; г) 2(m - n); е) m - cd. | + | 426. Прочитайте выражение: |
| | + | |
| | + | а) а • (с + d); в) 3(m+ n); д) аb + с; <br>б) (4 - а) • 8; г) 2(m - n); е) m - cd. |
| | | | |
| | 427. Найдите значение выражения: | | 427. Найдите значение выражения: |
| Строка 89: |
Строка 125: |
| | 428. Велосипедист ехал а ч со скоростью 12 км/ч и 2 ч со скоростью 8 км/ч. Сколько километров проехал велосипедист за это время? Составьте выражение для решения задачи и найдите его значение при а = 1; 2; 4. | | 428. Велосипедист ехал а ч со скоростью 12 км/ч и 2 ч со скоростью 8 км/ч. Сколько километров проехал велосипедист за это время? Составьте выражение для решения задачи и найдите его значение при а = 1; 2; 4. |
| | | | |
| - | 429. Составьте выражение по условию задачи: <br>а) Из 6 книжных полок составлен шкаф. Высота каждой полки х см. Найдите высоту шкафа. Найдите значение выражения при х = 28; 33. <br>б) За один рейс автомашина МАЗ-25 перевозит 25 т груза. Сколько груза она перевезет за k рейсов? Найдите значение выражения при k = 10; 5; 0. | + | 429. Составьте выражение по условию задачи: |
| | + | |
| | + | а) Из 6 книжных полок составлен шкаф. Высота каждой полки х см. Найдите высоту шкафа. Найдите значение выражения при х = 28; 33. <br>б) За один рейс автомашина МАЗ-25 перевозит 25 т груза. Сколько груза она перевезет за k рейсов? Найдите значение выражения при k = 10; 5; 0. |
| | | | |
| | 430. Цена одного волейбольного мяча х р., а баскетбольного мяча у р. Что означают выражения: Зх; 4у; bх + 2у; 15x - 2у; 4(х + у)? | | 430. Цена одного волейбольного мяча х р., а баскетбольного мяча у р. Что означают выражения: Зх; 4у; bх + 2у; 15x - 2у; 4(х + у)? |
| Строка 109: |
Строка 147: |
| | 436. Вычислите устно: | | 436. Вычислите устно: |
| | | | |
| - | [[Image:15-06-142.jpg]] | + | [[Image:15-06-142.jpg|480px|Задание]] |
| | | | |
| | <br>437. Какое число пропущено? | | <br>437. Какое число пропущено? |
| | | | |
| - | [[Image:15-06-143.jpg]]<br><br>438. Восстановите цепочку вычислений: | + | [[Image:15-06-143.jpg|480px|Задание]]<br><br>438. Восстановите цепочку вычислений: |
| | | | |
| - | [[Image:15-06-144.jpg]]<br><br>439. Угадайте корни уравнения: | + | [[Image:15-06-144.jpg|480px|Задание]]<br><br>439. Угадайте корни уравнения: |
| | | | |
| - | <br>а) х + х = 64; б) 58 + у + у + у = 58; в) а + 2 = а - 1.
| + | а) х + х = 64; б) 58 + у + у + у = 58; в) а + 2 = а - 1. |
| | | | |
| | 440. Придумайте задачу, которая решалась бы с помощью уравнения: | | 440. Придумайте задачу, которая решалась бы с помощью уравнения: |
| | | | |
| - | а) х+ 15 = 45; | + | а) х+ 15 = 45; |
| | | | |
| | б) у - 12 = 18. | | б) у - 12 = 18. |
| Строка 147: |
Строка 185: |
| | 447. Решите задачу: | | 447. Решите задачу: |
| | | | |
| - | а) В корзине несколько грибов. После того как из нее вынули 10 грибов, а затем в нее положили 14 грибов, в ней стало 85 грибов. Сколько грибов было <br>в корзине первоначально? <br>б) У мальчика было 16 почтовых марок. Он купил еще несколько марок, после этого подарил младшему брату 23 марки, и у него осталось 19 марок. <br>Сколько марок купил мальчик? | + | а) В корзине несколько грибов. После того как из нее вынули 10 грибов, а затем в нее положили 14 грибов, в ней стало 85 грибов. Сколько грибов было в корзине первоначально? |
| | + | |
| | + | б) У мальчика было 16 почтовых марок. Он купил еще несколько марок, после этого подарил младшему брату 23 марки, и у него осталось 19 марок. Сколько марок купил мальчик? |
| | | | |
| | 448. Упростите выражение: | | 448. Упростите выражение: |
| Строка 155: |
Строка 195: |
| | 449. Найдите значение выражения: | | 449. Найдите значение выражения: |
| | | | |
| - | 1) 7480 - 6480 : 120 + 80; | + | 1) 7480 - 6480 : 120 + 80; |
| | | | |
| | 2) 1110 + 6890 : 130 - 130. | | 2) 1110 + 6890 : 130 - 130. |
| Строка 171: |
Строка 211: |
| | 452. В магазин привезли 250 коробок, в каждой коробке по 54 пачки печенья. Какова масса всего печенья, если масса одной пачки 150 г? | | 452. В магазин привезли 250 коробок, в каждой коробке по 54 пачки печенья. Какова масса всего печенья, если масса одной пачки 150 г? |
| | | | |
| - | 453. В треугольнике ABC сторона АВ равна 27 см, и она больше стороны ВС в 3 раза. Найдите длину стороны АС, если периметр треугольника <br>ABC равен 61 см. | + | 453. В треугольнике ABC сторона АВ равна 27 см, и она больше стороны ВС в 3 раза. Найдите длину стороны АС, если периметр треугольника ABC равен 61 см. |
| | | | |
| - | 454. Один станок-автомат производит 12 деталей в минуту, а другой — 15 таких же деталей. Сколько всего деталей будет изготовлено за 20 мин <br>работы первого станка и 15 мин работы второго станка? | + | 454. Один станок-автомат производит 12 деталей в минуту, а другой — 15 таких же деталей. Сколько всего деталей будет изготовлено за 20 мин работы первого станка и 15 мин работы второго станка? |
| | | | |
| | 455. Выполните умножение: | | 455. Выполните умножение: |
| Строка 189: |
Строка 229: |
| | 459. Сравните, не вычисляя, произведения (ответ запишите с помощью знака <): | | 459. Сравните, не вычисляя, произведения (ответ запишите с помощью знака <): |
| | | | |
| - | а) 245 • 611 и 391 • 782; | + | а) 245 • 611 и 391 • 782; |
| | | | |
| | б) 8976 • 1240 и 6394 • 906. | | б) 8976 • 1240 и 6394 • 906. |
| Строка 205: |
Строка 245: |
| | а) (х + 27) - 12 = 42; в) г - 35 - 64 = 16; <br>б) 115 - (35 + у) = 39; г) 28 - t + 35 = 53. | | а) (х + 27) - 12 = 42; в) г - 35 - 64 = 16; <br>б) 115 - (35 + у) = 39; г) 28 - t + 35 = 53. |
| | | | |
| - | 463. Сосчитайте, сколько четверок и сколько пятерок на рисунке 48, но только по особому правилу — считать нужно подряд и четверки, и пятерки: «Первая четверка, первая пятерка, вторая четверка, третья четверка, вторая пятерка и т. д.». Если сразу не удастся сосчитать, возвращайтесь к этому заданию еще и еще раз. <br>[[Image:15-06-145.jpg]]<br><br> | + | 463. Сосчитайте, сколько четверок и сколько пятерок на рисунке 48, но только по особому правилу — считать нужно подряд и четверки, и пятерки: «Первая четверка, первая пятерка, вторая четверка, третья четверка, вторая пятерка и т. д.». Если сразу не удастся сосчитать, возвращайтесь к этому заданию еще и еще раз. |
| | + | |
| | + | <br>[[Image:15-06-145.jpg|480px|Задание]]<br> |
| | | | |
| | <br> ''Н.Я. ВИЛЕНКИН, B. И. ЖОХОВ, А. С. ЧЕСНОКОВ, C. И. ШВАРЦБУРД, Математика 5 класс, Учебник для общеобразовательных учреждений'' <br> | | <br> ''Н.Я. ВИЛЕНКИН, B. И. ЖОХОВ, А. С. ЧЕСНОКОВ, C. И. ШВАРЦБУРД, Математика 5 класс, Учебник для общеобразовательных учреждений'' <br> |
| | + | |
| | + | |
| | | | |
| | <sub>Сборник конспектов уроков по математике [[Математика|скачать]], календарно-тематическое планирование, учебники по всем предметам [[Гипермаркет знаний - первый в мире!|онлайн]]</sub> | | <sub>Сборник конспектов уроков по математике [[Математика|скачать]], календарно-тематическое планирование, учебники по всем предметам [[Гипермаркет знаний - первый в мире!|онлайн]]</sub> |
| Строка 214: |
Строка 258: |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | '''<u></u>''' | | '''<u></u>''' |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Версия 06:57, 5 октября 2012
Гипермаркет знаний>>Математика>>Математика 5 класс>>Математика:Умножение натуральных чисел и его свойства
Умножение натуральных чисел и его свойства
Если концертный зал освещается тремя люстрами по 25 лампочек в каждой, то всего лампочек в этих люстрах будет 25 + 25 + 25, то есть 75.
Сумму, в которой все слагаемые равны друг другу, записывают короче: вместо 25 + 25 + 25 пишут 25 • 3.
Значит, 25 • 3 = 75. Число 75 называют произведением чисел 25 и 3, а числа 25 и 3 называют множителями.
Умножить число m на натуральное число n — значит найти сумму n слагаемых, каждое из которых равно m.
Выражение m • n и значение этого выражения называют произведением чисел m и n. Числа m и n называют множителями.
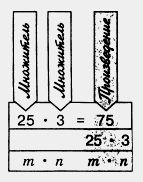
Произведения 7 • 4 и 4 • 7 равны одному и тому же числу 28 (рис. 46).
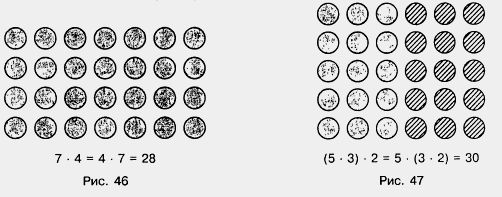
1. Произведение двух чисел не изменяется при перестановке множителей. Это свойство умножения называют переместительным. С помощью букв его записывают так:
а • b = b • а.
Произведения (5 • 3) • 2 = 15 • 2 и 5 • (3 - 2) = 5 • 6 имеют одно и то же значение 30. Значит, 5 • (3 • 2) = (5 • 3) • 2 (рис. 47).
2. Чтобы умножить число на произведение двух чисел, можно сначала умножить его на первый множитель, а потом полученное произведение умножить на второй множитель.
Это свойство умножения называют сочетательным. С помощью букв его записывают так:
a • (b • с) = (а • b) • с.
Сумма n слагаемых, каждое из которых равно 1, равна n. Поэтому верно равенство 1 • n = n.
Сумма п слагаемых, каждое из которых равно нулю, равна нулю. Поэтому верно равенство 0 • п = 0.
Чтобы переместительное свойство умножения было верно при n = 1 и n = 0, условились, что m • 1 = m и m • 0 = 0.
Перед буквенными множителями обычно не пишут знак умножения: вмето 8 • х пишут 8х, вместо a • b пишут ab.
Опускают знак умножения и перед скобками. Например, вместо 2 • (а + b) пишут 2(а + b), а вместо (х + 2) • (y + 3) пишут (х + 2)(у + 3).
Вместо (аb)с пишут abc.
Когда в записи произведения нет скобок, умножение выполняют по порядку слева направо.
Что значит умножить одно натуральное число на другое?
Как называют числа, которые перемножают?
Как называют результат умножения?
Чему равно 1 • n? Чему равно О • n?
Сформулируйте переместительное свойство умножения. Запишите его а а 0 с помощью букв. • 4г •
Сформулируйте сочетательное свойство умножения. Запишите его °$ tf 9* с помощью букв.
В каких случаях можно опустить знак умножения?
Чему равно произведение m • 1 ?
Чему равно произведение m • 0?
404. Представьте в виде произведения сумму:
а) 707 + 707 + 707;
б) 50 4- 50 + 50 + 50 + 50 + 50;
b) x + x + x + x + x + x
405. Представьте в виде суммы произведение:
а) 712 • 3; в) (х + у) • 4;
б) а • 6; г) (k + m + 4) • 2.

406. Вместо слов «представьте в виде произведения» говорят «разложите на множители». Разложите всеми способами на два множителя число 12.
407. Сколько времени Борис решал 6 уравнений, если на каждое уравнение ему требовалось 2 мин 30 с?
408. Точка С лежит на отрезке АВ. Найдите длину отрезка АВ, если АС = 8 см, а длина отрезка СВ в 3 раза больше длины отрезка АС.
409. Отрезок АВ разбит на 17 отрезков, по 7 см каждый. Найдите длину отрезка АВ.
410. В двух ящиках лежат помидоры. Во втором ящике в 3 раза больше помидоров, чем в первом. Сколько помидоров в обоих ящиках, если в первом ящике 12 кг?
411. Сережа старше своей сестры на 5 лет, но моложе отца в 3 раза. Сколько лет Сереже и сколько лет его отцу, если Сережиной сестре 8 лет?
412. Найдите значение произведения:
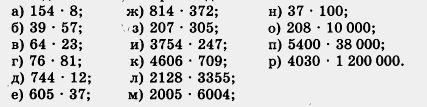
413. Найдите значение выражения:
а) 305 + 305 + 305 + 305 + 73;
б) 615 + 615 + 125 + 125 + 125;
в) 2011 + 402 + 402 + 402 + 402 + 402;
г) 58 + 58 + 58 + 58 + 58 + 720 + 720.
414. Вместо звездочек поставьте пропущенные цифры:
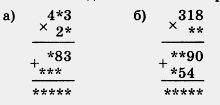
415. Выполните действия, применив сочетательное свойство умножения:
а) 50 • (2 • 764); в) 125 • (4 • 80);
б) (111 • 2) • 35; г) (402 • 125) • 8.
416. Вычислите, выбрав удобный порядок действий:
а) 483 • 2 • 5; в) 25 • 86 • 4;
б) 4 • 5 • 333; г) 250 • 3 • 40.
417. В магазин привезли 5 ящиков с красками. В каждом ящике 144 коробки, а в каждой коробке 12 тюбиков с красками. Сколько тюбиков привезли в магазин? Решите задачу двумя способами.
418. Столяр и его помощник должны сделать 217 рам. Столяр в день делает 18 рам, а его помощник — 13. Сколько рам им останется сделать после двух дней, работы? четырех дней работы? семи дней работы?
419. Для покраски двери требуется 800 г белил, а для покраски окна на 200 г меньше. Сколько белил потребуется, чтобы покрасить 3 окна и 4 двери?
420. Составьте выражение для решения задачи:
а) Построили 5 коттеджей по 80 м2 жилой площади и 2 коттеджа по 140 м2. Какова жилая площадь всех этих коттеджей?
б) Масса контейнера с четырьмя книжными шкафами 3 ц. Какова масса пустого контейнера, если масса одного шкафа 58 кг?
421. Привезли 12 ящиков яблок, по 30 кг в каждом, и 8 ящиков груш, по 40 кг в каждом. Какой смысл имеют следующие выражения:
а) 30 • 12; в) 40 • 8; д) 30 • 12 + 40 • 8;
б) 12 - 8; г) 40 - 30; е) 30 • 12 - 40 • 8?
422. Выполните действия:
а) (527 - 393) • 8; г) 54 • 23 • 35;
б) 38 • 65 - 36 • 63; д) (247 - 189) • (69 + 127);
в) 127 • 15 + 138 • 32; е) (1203 + 2837 - 1981) • 21.
423. Запишите произведение:
а) 8 и х; б) 12 + а и 16; в) 25 -m и 28 + n г) а + b и m.
424. Укажите множители в произведении:
а) Зт; в) 4ab; д) (m + n)(k - 3);
б) 6(х + р); г) (х - у) • 14; е) 5k(m + а).
425. Запишите выражение:
а) произведение m и n;
б) утроенная сумма а и b;
в) сумма произведений чисел 6 и х и чисел 8 и у;
г) произведение разности чисел а и b и числа с.
426. Прочитайте выражение:
а) а • (с + d); в) 3(m+ n); д) аb + с;
б) (4 - а) • 8; г) 2(m - n); е) m - cd.
427. Найдите значение выражения:
а) 8а + 250 при а = 12; 15;
б) 14(6 + 12) при b = 13; 18.
428. Велосипедист ехал а ч со скоростью 12 км/ч и 2 ч со скоростью 8 км/ч. Сколько километров проехал велосипедист за это время? Составьте выражение для решения задачи и найдите его значение при а = 1; 2; 4.
429. Составьте выражение по условию задачи:
а) Из 6 книжных полок составлен шкаф. Высота каждой полки х см. Найдите высоту шкафа. Найдите значение выражения при х = 28; 33.
б) За один рейс автомашина МАЗ-25 перевозит 25 т груза. Сколько груза она перевезет за k рейсов? Найдите значение выражения при k = 10; 5; 0.
430. Цена одного волейбольного мяча х р., а баскетбольного мяча у р. Что означают выражения: Зх; 4у; bх + 2у; 15x - 2у; 4(х + у)?
431. Составьте задачу по выражению:
а) (80 + 60) -7; в) 28 • 4 + 35 • 5;
б) (65 - 40) -4; г) 96 • 5 - 82 • 3.
432. На вершину холма ведут пять тропинок. Сколько существует способов подняться на холм и спуститься с него, если подниматься и спускаться по разным тропинкам?
433. Какое из произведений больше: 67 • 2 или 67 • 3? Объясните, почему это так. Объясните, почему 190 • 8 < 195 • 12. Сделайте вывод.
434. Расставьте, не выполняя умножения, в порядке возрастания произведения: 56 • 24; 56 • 49; 13 • 24; 13 • 11; 74 • 49; 7 • 11.
435. Докажите, что:
а) 20 • 30 < 23 • 35 < 30 • 40;
б) 600 • 800 < 645 • 871 < 700 • 900;
в) 1200 < 36 • 42 < 2000;
г) 45 000 < 94 • 563 < 60 000.
436. Вычислите устно:
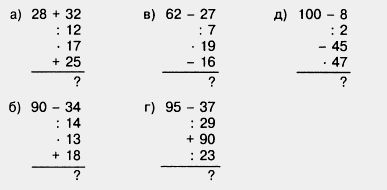
437. Какое число пропущено?
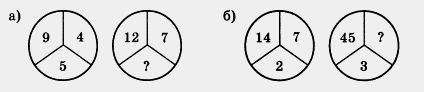
438. Восстановите цепочку вычислений:
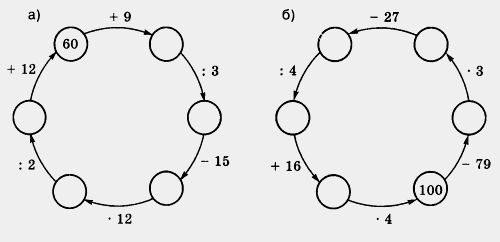
439. Угадайте корни уравнения:
а) х + х = 64; б) 58 + у + у + у = 58; в) а + 2 = а - 1.
440. Придумайте задачу, которая решалась бы с помощью уравнения:
а) х+ 15 = 45;
б) у - 12 = 18.
441. Сколько четырехзначных чисел можно составить из нечетных цифр, ели цифры в записи числа не повторяются?
442. Среди чисел 1, 0, 5, 11,9 найдите корни уравнения:
а) х + 19 = 30; в) 30 + х = 32 - х
б) 27 - х = 27 + х; г) 10 + х + 2 = 15 + х - 3.
443. Назовите несколько свойств луча. Какие из этих свойств есть у прямой?
444. Придумайте способ, с помощью которого можно быстро и просто вычислить значение выражения:
39 - 37 + 35 - 33 + 31 - 29 + 27 - 25 + ... + 11 - 9 + 7 - 5 + 3 - 1.
445. Решите уравнение:
а) 127 + у = 357 - 85; в) 144 - у - 54 = 37;
б) 125 + у - 85 = 65; г). 52 + у + 87 = 159.
446. При каком значении буквы верно равенство:
а) 34 + а = 34; г) 58 - d = 0; ж) k - k = 0;
б) b + 18 = 18; д) m + 0 = 0; з) l + I = 0?
в) 75 - с = 75; е) 0 - n = 0;
447. Решите задачу:
а) В корзине несколько грибов. После того как из нее вынули 10 грибов, а затем в нее положили 14 грибов, в ней стало 85 грибов. Сколько грибов было в корзине первоначально?
б) У мальчика было 16 почтовых марок. Он купил еще несколько марок, после этого подарил младшему брату 23 марки, и у него осталось 19 марок. Сколько марок купил мальчик?
448. Упростите выражение:
1) (138 + m) - 95; 3) (х - 39) + 65;
2) (198 + n) - 36; 4) (у - 56) + 114.
449. Найдите значение выражения:
1) 7480 - 6480 : 120 + 80;
2) 1110 + 6890 : 130 - 130.
450. Найдите значение выражения:
а) 704 + 704 + 704 + 704;
б) 542 + 542 + 542 + 618 + 618.
451. Представьте в виде суммы произведение:
а) 24-4; б) k • 8; в) (x + y)• 4: г) (2а - b) • 5.
452. В магазин привезли 250 коробок, в каждой коробке по 54 пачки печенья. Какова масса всего печенья, если масса одной пачки 150 г?
453. В треугольнике ABC сторона АВ равна 27 см, и она больше стороны ВС в 3 раза. Найдите длину стороны АС, если периметр треугольника ABC равен 61 см.
454. Один станок-автомат производит 12 деталей в минуту, а другой — 15 таких же деталей. Сколько всего деталей будет изготовлено за 20 мин работы первого станка и 15 мин работы второго станка?
455. Выполните умножение:
а) 56 • 24; в) 235 • 48; д) 203 • 504; ж) 2103 • 7214;
б) 37 • 85; г) 37 • 129; е) 210 • 3500; з) 5008 • 3020.
456. С одной и той же станции в одно и то же время вышли в противоположных направлениях два поезда. Скорость одного поезда 50 км/ч, а другого 85 км/ч. Какое расстояние будет между поездами через 3 ч?
457. От деревни до города велосипедист ехал 4 ч со скоростью 12 км/ч. Сколько времени он потратит на обратный путь по той же дороге, если увеличит скорость на 4 км/ч?
458. Придумайте задачу по выражению:
а) 120 + 65-2; б) 168 -43-2; в) 15 • 4 + 12 • 4.
459. Сравните, не вычисляя, произведения (ответ запишите с помощью знака <):
а) 245 • 611 и 391 • 782;
б) 8976 • 1240 и 6394 • 906.
460. Запишите в порядке возрастания произведения:
172 • 191; 85 • 91; 85 • 104; 36 • 91; 36 • 75; 172 • 104.
461. Вычислите:
а) (18 384 4- 19 847) • (384 - 201 - 183);
б) (2839 - 939) • (577 : 577).
462. Решите уравнение:
а) (х + 27) - 12 = 42; в) г - 35 - 64 = 16;
б) 115 - (35 + у) = 39; г) 28 - t + 35 = 53.
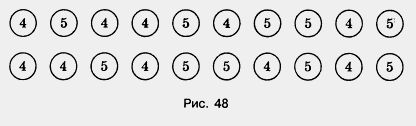
463. Сосчитайте, сколько четверок и сколько пятерок на рисунке 48, но только по особому правилу — считать нужно подряд и четверки, и пятерки: «Первая четверка, первая пятерка, вторая четверка, третья четверка, вторая пятерка и т. д.». Если сразу не удастся сосчитать, возвращайтесь к этому заданию еще и еще раз.
Н.Я. ВИЛЕНКИН, B. И. ЖОХОВ, А. С. ЧЕСНОКОВ, C. И. ШВАРЦБУРД, Математика 5 класс, Учебник для общеобразовательных учреждений
Сборник конспектов уроков по математике скачать, календарно-тематическое планирование, учебники по всем предметам онлайн
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|