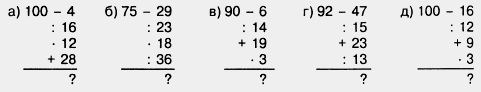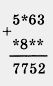|
|
| Строка 3: |
Строка 3: |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 5 класс|Математика 5 класс]]>>Математика:Степень числа. Квадрат и куб числа''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 5 класс|Математика 5 класс]]>>Математика:Степень числа. Квадрат и куб числа''' |
| | | | |
| - | <br>
| |
| | | | |
| - | ''' Степень числа. Квадрат и куб числа '''<br> | + | '''Степень числа. Квадрат и куб числа''' |
| | + | |
| | + | <br>Мы знаем, что сумму, в которой все слагаемые равны друг другу, можно записать короче — в виде произведения. Например, вместо 3 + 3 + 3 + 3 + 3 пишут 3 • 5. В этом произведении число 5 показывает, сколько слагаемых было в [http://xvatit.com/busines/ '''сумме''']. |
| | | | |
| - | <br>Мы знаем, что сумму, в которой все слагаемые равны друг другу, можно записать короче — в виде произведения. Например, вместо 3 + 3 + 3 + 3 + 3 <br>пишут 3 • 5. В этом произведении число 5 показывает, сколько слагаемых было в сумме. <br>Произведение, в котором все множители равны друг другу, тоже записывают короче: вместо 2 • 2 • 2 • 2 • 2 • 2 пишут 26. Запись 26 читают: «два в шестой степени». В этой записи число 2 называют '''основанием степени''', число 6, которое показывает, сколько множителей было в произведении, — '''показателем степени''', а выражение 26 называют '''степенью'''.
| + | Произведение, в котором все множители равны друг другу, тоже записывают короче: вместо 2 • 2 • 2 • 2 • 2 • 2 пишут 26. Запись 26 читают: «два в шестой степени». В этой записи число 2 называют основанием степени, число 6, которое показывает, сколько множителей было в произведении, — показателем степени, а выражение 26 называют степенью. |
| | | | |
| - | '''Пример 1.''' Запишем произведения в виде степени и найдем их значения: <br> | + | '''Пример 1.''' Запишем произведения в виде степени и найдем их значения: <br> |
| | | | |
| - | 3 • 3 • 3 • 3 = 34 = 81; <br>5 . 5 • 5 = 53= 125; <br>2 • 2 • 2 • 2 • 2 • 2 = 26 = 64. <br> | + | 3 • 3 • 3 • 3 = 34 = 81; <br>5 . 5 • 5 = 53= 125; <br>2 • 2 • 2 • 2 • 2 • 2 = 26 = 64. <br> |
| | | | |
| - | торую степень числа часто называют иначе. Произведение 3 • 3 называют квадратом числа 3 и обозначают З<sup>2</sup>. <br>Произведение n и n называют '''квадратом числа''' n и обозначают n2 (читают: «эн в квадрате»). Итак, n<sup>2</sup> = n • n. | + | торую степень числа часто называют иначе. Произведение 3 • 3 называют квадратом числа 3 и обозначают З<sup>2</sup>. <br>Произведение n и n называют квадратом числа n и обозначают n2 (читают: «эн в квадрате»). Итак, n<sup>2</sup> = n • n. |
| | | | |
| - | Например, 172 = 17 • 17 = 289. <br> | + | Например, 172 = 17 • 17 = 289. <br> |
| | | | |
| | Таблица квадратов первых 10 натуральных чисел имеет следующий вид: | | Таблица квадратов первых 10 натуральных чисел имеет следующий вид: |
| | | | |
| - | [[Image:16-06-1.jpg]]<br> | + | [[Image:16-06-1.jpg|480px|Задание]]<br> |
| | | | |
| - | Третья степень числа также имеет и иное название. Произведение 4 • 4 • 4 называют кубом числа 4 и обозначают 4<sup>3</sup>. Произведение n • n • n называют '''кубом числа''' n и обозначают n<sup>3 </sup>(читают: 5 «эн в кубе»). <br>Итак, n<sup>3</sup> = n • n • n. <br>Например, 8<sup>3</sup> = 8 •8 •8 = 64-8 = 512. | + | Третья степень числа также имеет и иное название. Произведение 4 • 4 • 4 называют кубом числа 4 и обозначают 4<sup>3</sup>. Произведение n • n • n называют кубом числа n и обозначают n<sup>3 </sup>(читают: 5 «эн в кубе»). |
| | | | |
| - | Таблица кубов первых 10 натуральных чисел имеет вид: <br>
| + | Итак, n<sup>3</sup> = n • n • n. |
| | | | |
| - | [[Image:16-06-2.jpg]]<br><br>Первую степень числа считают равной самому числу: <br> 7<sup>1</sup> = 7, 16<sup>1</sup> = 16, 1<sup>1</sup> = 1. <br>Показатель степени 1 обычно не пишут. <br>Если в числовое выражение входят степени чисел, то их значения вычисляют до выполнения остальных действий.
| + | Например, 8<sup>3</sup> = 8 •8 •8 = 64-8 = 512. |
| | | | |
| - | '''Пример 2.''' Найдем значение выражения (4 + З)<sup>2</sup> • 5<sup>2</sup> - 8<sup>3</sup> + 2<sup>6</sup>. <br>Решение.
| + | Таблица кубов первых 10 натуральных чисел имеет вид: <br> |
| | | | |
| - | (4 + З)<sup>2</sup> • 5<sup>2</sup> - 8<sup>3</sup> + 2<sup>6</sup> = 7<sup>2</sup> - 25 - 512 + 64= 49 • 25 - 512 + 64 = 1225 - 512 + 64 = 777. <br>
| + | [[Image:16-06-2.jpg|480px|Задание]]<br><br>Первую степень числа считают равной самому числу: |
| | | | |
| - | '''Что такое квадрат числа? <br>Что такое куб числа? '''<br>'''Назовите основание и показатель степени: б7, 123, 410, 152, 81. '''<br><br>652. Составьте таблицу квадратов чисел от 11 до 20. <br>
| + | 7<sup>1</sup> = 7, 16<sup>1</sup> = 16, 1<sup>1</sup> = 1. |
| | | | |
| - | 653. Представьте в виде степени произведение: <br>
| + | Показатель степени 1 обычно не пишут. |
| | | | |
| - | а) 6 • 6 • 6 • 6 • 6 • 6 • 6; <br>в) 73 • 73; <br>
| + | Если в числовое выражение входят степени чисел, то их значения вычисляют до выполнения остальных действий. |
| | | | |
| - | б) 25 • 25 • 25 • 25 • 25; <br>г) 11 • 11 • 11 • 11;<br>д) 9 • 9 • 9; <br>е) m• m • m • m • m • m; <br> | + | '''Пример 2.''' Найдем значение выражения (4 + З)<sup>2</sup> • 5<sup>2</sup> - 8<sup>3</sup> + 2<sup>6</sup>. |
| | + | |
| | + | Решение. |
| | + | |
| | + | (4 + З)<sup>2</sup> • 5<sup>2</sup> - 8<sup>3</sup> + 2<sup>6</sup> = 7<sup>2</sup> - 25 - 512 + 64= 49 • 25 - 512 + 64 = 1225 - 512 + 64 = 777. <br> |
| | + | |
| | + | ''Что такое квадрат числа? <br>Что такое куб числа? <br>Назовите основание и показатель степени: б7, 123, 410, 152, 81. ''<br><br>652. Составьте таблицу квадратов чисел от 11 до 20. <br> |
| | + | |
| | + | 653. Представьте в виде степени произведение: <br> |
| | + | |
| | + | а) 6 • 6 • 6 • 6 • 6 • 6 • 6; <br>в) 73 • 73; <br> |
| | + | |
| | + | б) 25 • 25 • 25 • 25 • 25; <br>г) 11 • 11 • 11 • 11;<br>д) 9 • 9 • 9; <br>е) m• m • m • m • m • m; <br> |
| | | | |
| | ж) х • х • х; | | ж) х • х • х; |
| Строка 43: |
Строка 56: |
| | з) у• у •у• у• у• у• у •у; | | з) у• у •у• у• у• у• у •у; |
| | | | |
| - | и) k • к<br> | + | и) k • к<br> |
| | | | |
| | к) n • n • n •n • n; | | к) n • n • n •n • n; |
| | | | |
| - | л) (х + 1)(х + 1)(х + 1); <br> | + | л) (х + 1)(х + 1)(х + 1); <br> |
| | | | |
| - | м) (7 - n)(7 - n). <br> | + | м) (7 - n)(7 - n). <br> |
| | | | |
| - | <br>654. Представьте в виде произведения степень: <br> | + | <br>654. Представьте в виде произведения степень: <br> |
| | | | |
| - | а) 7<sup>5</sup>; г) 1000<sup>2</sup>; ж) k<sup>3</sup>; к) (m + 2)<sup>4</sup>; <br>б) 12<sup>4</sup>; д) 60<sup>7</sup>; з) а<sup>8</sup>; л) (а - 7)<sup>2</sup>; <br>в) 15<sup>3</sup>; е) n<sup>9</sup>; и) х<sup>2</sup>; м) (х 4- у)<sup>3</sup>. <br> | + | а) 7<sup>5</sup>; г) 1000<sup>2</sup>; ж) k<sup>3</sup>; к) (m + 2)<sup>4</sup>; <br>б) 12<sup>4</sup>; д) 60<sup>7</sup>; з) а<sup>8</sup>; л) (а - 7)<sup>2</sup>; <br>в) 15<sup>3</sup>; е) n<sup>9</sup>; и) х<sup>2</sup>; м) (х 4- у)<sup>3</sup>. <br> |
| | | | |
| - | 655. Найдите значения: 252; 1002; 103; II3; 123; 153. <br> | + | 655. Найдите значения: 252; 1002; 103; II3; 123; 153. <br> |
| | | | |
| - | 656. Найдите значения степеней: 25; 106; I20; З4; 411; 44. <br> | + | 656. Найдите значения степеней: 25; 106; I20; З4; 411; 44. <br> |
| | | | |
| - | 657. Найдите значение выражения: <br> | + | 657. Найдите значение выражения: <br> |
| | | | |
| - | а) З<sup>2</sup> • 18; д) 7 + 4<sup>3</sup>; и) 5<sup>2</sup> • 2<sup>3</sup>; <br>б) 5 + 4<sup>2</sup>; е) 7<sup>3</sup> + 4; к) 2<sup>5</sup> + З<sup>4</sup>; <br>в) (5 + 4)<sup>2</sup>; ж) (7 + 4)<sup>3</sup>; л) (30 : З)<sup>5</sup> - 100<sup>3</sup>; <br>г) 5<sup>2</sup> + 4<sup>2</sup>; з) (7<sup>3</sup> - 4<sup>3</sup>) : (7 - 4); м) (10<sup>2</sup> - 2<sup>6</sup>) : 6 + 1<sup>10</sup>. <br> | + | а) З<sup>2</sup> • 18; д) 7 + 4<sup>3</sup>; и) 5<sup>2</sup> • 2<sup>3</sup>; <br>б) 5 + 4<sup>2</sup>; е) 7<sup>3</sup> + 4; к) 2<sup>5</sup> + З<sup>4</sup>; <br>в) (5 + 4)<sup>2</sup>; ж) (7 + 4)<sup>3</sup>; л) (30 : З)<sup>5</sup> - 100<sup>3</sup>; <br>г) 5<sup>2</sup> + 4<sup>2</sup>; з) (7<sup>3</sup> - 4<sup>3</sup>) : (7 - 4); м) (10<sup>2</sup> - 2<sup>6</sup>) : 6 + 1<sup>10</sup>. <br> |
| | | | |
| - | 658. Пользуясь таблицами квадратов и кубов чисел, найдите значение д, если: <br> | + | 658. Пользуясь таблицами квадратов и кубов чисел, найдите значение д, если: <br> |
| | | | |
| - | 121 - n<sup>2</sup>; n<sup>2</sup> = 196; n<sup>2</sup> = 10 000; 125 = n<sup>3</sup>; n<sup>3</sup> = 512. <br> | + | 121 - n<sup>2</sup>; n<sup>2</sup> = 196; n<sup>2</sup> = 10 000; 125 = n<sup>3</sup>; n<sup>3</sup> = 512. <br> |
| | | | |
| - | 659. Вычислите устно: <br> | + | 659. Вычислите устно: <br> |
| | | | |
| - | [[Image:16-06-3.jpg]]<br> | + | [[Image:16-06-3.jpg|480px|Задание]]<br> |
| | | | |
| - | <br>660. Угадайте корни уравнения: <br> | + | <br>660. Угадайте корни уравнения: <br> |
| | | | |
| - | а) х • х = 25; в) а • а = 1; <br>б) у • у = 81; г)Ь•Ь•Ь = 0.<br> | + | а) х • х = 25; в) а • а = 1; <br>б) у • у = 81; г)Ь•Ь•Ь = 0.<br> |
| | | | |
| - | 661. Какие цифры заменены звездочками? <br> | + | 661. Какие цифры заменены звездочками? <br> |
| | | | |
| - | [[Image:16-06-4.jpg]]<br>Подумайте, какие уравнения пришлось решать для нахождения 7752 неизвестных цифр. <br> | + | [[Image:16-06-4.jpg|80px|Задание]]<br>Подумайте, какие уравнения пришлось решать для нахождения 7752 неизвестных цифр. <br> |
| | | | |
| - | 662. Каков порядок выполнения действий при вычислении значения выражения: <br> | + | 662. Каков порядок выполнения действий при вычислении значения выражения: <br> |
| | | | |
| - | а) 160 + 37 - 20; <br> | + | а) 160 + 37 - 20; <br> |
| | | | |
| - | б) 90 - 60 : 15; <br> | + | б) 90 - 60 : 15; <br> |
| | | | |
| - | в) 80 - 15 + 25? <br> | + | в) 80 - 15 + 25? <br> |
| | | | |
| - | Если возможно, укажите другой порядок действий, приводящий к тому же результату. <br> | + | Если возможно, укажите другой порядок действий, приводящий к тому же результату. <br> |
| | | | |
| - | 663. Составьте выражение по следующей программе: <br> | + | 663. Составьте выражение по следующей программе: <br> |
| | | | |
| - | 1. Разделить 58 344 на 429. <br>2. 215 умножить на 48. <br>3. Сложить результаты команд 1 и 2. <br>Найдите значение получившегося выражения. <br> | + | 1. Разделить 58 344 на 429. <br>2. 215 умножить на 48. <br>3. Сложить результаты команд 1 и 2. <br>Найдите значение получившегося выражения. <br> |
| | | | |
| - | 664. Составьте схему вычисления выражения: <br> | + | 664. Составьте схему вычисления выражения: <br> |
| | | | |
| - | (39 • 71 + 25 • 95) - (248 : 4 - 176 : 11). <br> | + | (39 • 71 + 25 • 95) - (248 : 4 - 176 : 11). <br> |
| | | | |
| - | 665. Решите задачу: <br>1) Сумма двух чисел 549. Одно из них в 8 раз больше другого. Найдите эти числа. <br>2) Сумма двух чисел 378. Одно из них в 8 раз меньше другого. Найдите эти числа. <br>3) Разность двух чисел 342. Одно из них в 7 раз меньше другого. Найдите эти числа. <br>4) Разность двух чисел 516. Одно из них в 7 раз больше другого. Найдите эти числа. <br> | + | 665. Решите задачу: |
| | | | |
| - | 666. Найдите значения:<br>
| + | 1) Сумма двух чисел 549. Одно из них в 8 раз больше другого. Найдите эти числа. <br>2) Сумма двух чисел 378. Одно из них в 8 раз меньше другого. Найдите эти числа. <br>3) Разность двух чисел 342. Одно из них в 7 раз меньше другого. Найдите эти числа. <br>4) Разность двух чисел 516. Одно из них в 7 раз больше другого. Найдите эти числа. <br> |
| | | | |
| - | 18<sup>2</sup>; 53; 13<sup>2</sup>; 20<sup>3</sup>; 40<sup>2</sup>; 30<sup>3</sup>. <br>
| + | 666. Найдите значения:<br> |
| | | | |
| - | 667. Найдите значения: 2<sup>4</sup>; З<sup>3</sup>; 10<sup>5</sup>; 1<sup>12</sup>; 100<sup>4</sup>; 20<sup>6</sup>. <br>
| + | 18<sup>2</sup>; 53; 13<sup>2</sup>; 20<sup>3</sup>; 40<sup>2</sup>; 30<sup>3</sup>. <br> |
| | | | |
| - | 668. Найдите значение выражения: <br>
| + | 667. Найдите значения: 2<sup>4</sup>; З<sup>3</sup>; 10<sup>5</sup>; 1<sup>12</sup>; 100<sup>4</sup>; 20<sup>6</sup>. <br> |
| | | | |
| - | а) 9<sup>2</sup> + 19; е) (17 - 16)<sup>8</sup> + 2<sup>5</sup>; <br>б) 17<sup>2</sup> - 209; ж) 10<sup>6</sup> - 20<sup>4</sup>; <br>в) б<sup>3</sup> : 3; з) З<sup>4</sup> • 10<sup>4</sup>; <br>г) 2<sup>3</sup> • З<sup>2</sup>; и) 5<sup>4</sup> : 5<sup>2</sup>. <br>д) (15 - 7)<sup>2</sup> : 2<sup>3</sup>; <br>
| + | 668. Найдите значение выражения: <br> |
| | | | |
| - | 669. Из Москвы и Ростова-на-Дону одновременно вышли навстречу друг другу два поезда. Поезд из Москвы шел со скоростью 65 км/ч, а поезд из Ростова-на-Дону — со скоростью на 7 км/ч меньшей. На каком расстоянии друг от друга будут поезда через 6 ч после начала движения, если расстояние между Москвой и Ростовом-на-Дону 1230 км? <br>
| + | а) 9<sup>2</sup> + 19; е) (17 - 16)<sup>8</sup> + 2<sup>5</sup>; <br>б) 17<sup>2</sup> - 209; ж) 10<sup>6</sup> - 20<sup>4</sup>; <br>в) б<sup>3</sup> : 3; з) З<sup>4</sup> • 10<sup>4</sup>; <br>г) 2<sup>3</sup> • З<sup>2</sup>; и) 5<sup>4</sup> : 5<sup>2</sup>. <br>д) (15 - 7)<sup>2</sup> : 2<sup>3</sup>; <br> |
| | | | |
| - | 670. С двух станций, расстояние между которыми 720 км, вышли одновременно навстречу друг другу два поезда. Скорость первого поезда 75 км/ч, а скорость второго на 10 км/ч больше. На каком расстоянии друг от друга будут поезда через 4 ч? <br>
| + | 669. Из Москвы и Ростова-на-Дону одновременно вышли навстречу друг другу два поезда. Поезд из Москвы шел со скоростью 65 км/ч, а поезд из Ростова-на-Дону — со скоростью на 7 км/ч меньшей. На каком расстоянии друг от друга будут поезда через 6 ч после начала движения, если расстояние между Москвой и Ростовом-на-Дону 1230 км? <br> |
| | | | |
| - | 671. Составьте программу вычислений для нахождения значения выражения <br>
| + | 670. С двух станций, расстояние между которыми 720 км, вышли одновременно навстречу друг другу два поезда. Скорость первого поезда 75 км/ч, а скорость второго на 10 км/ч больше. На каком расстоянии друг от друга будут поезда через 4 ч? <br> |
| | | | |
| - | 67 392 : (3504 - 3408) + 19 232 : 601 <br>и изобразите ее схемой. Найдите значение выражения. <br>
| + | 671. Составьте программу вычислений для нахождения значения выражения <br> |
| | | | |
| - | 672. Выполните действия: <br>
| + | 67 392 : (3504 - 3408) + 19 232 : 601 <br>и изобразите ее схемой. Найдите значение выражения. <br> |
| | | | |
| - | 14 • (3600 • 18 - 239 200 : 46). <br><br>[[Image:16-06-5.jpg]]<br>Выдающийся российский математик академик Андреи Николаевич Колмогоров решил много сложнейших задач, совершил не одно открытие в различных разделах современной математики. Но радость своих первых математических «открытий» он познал рано. Андрей Николаевич рассказывал, что еще до поступления в гимназию в возрасте пяти-шести лет он любил придумывать задачи, подмечал интересные свойства чисел. Эти «открытия» публиковались в домашнем журнале. Вот одно из «открытий» шестилетнего Колмогорова. Он заметил, что <br>
| + | 672. Выполните действия: <br> |
| | + | |
| | + | 14 • (3600 • 18 - 239 200 : 46). <br> |
| | + | |
| | + | Выдающийся российский [http://xvatit.com/vuzi/ '''математик'''] академик Андреи Николаевич Колмогоров решил много сложнейших задач, совершил не одно открытие в различных разделах современной математики. Но радость своих первых математических «открытий» он познал рано. Андрей Николаевич рассказывал, что еще до поступления в гимназию в возрасте пяти-шести лет он любил придумывать задачи, подмечал интересные свойства чисел. Эти «открытия» публиковались в домашнем журнале. Вот одно из «открытий» шестилетнего Колмогорова. Он заметил, что <br> |
| | | | |
| | 1<sup>2</sup> = 1, 2<sup>2</sup> = 1+3, 3<sup>2</sup> = 1+3 + 5, 4<sup>2</sup> = 1+3 + 5 + 7. | | 1<sup>2</sup> = 1, 2<sup>2</sup> = 1+3, 3<sup>2</sup> = 1+3 + 5, 4<sup>2</sup> = 1+3 + 5 + 7. |
| | | | |
| - | 673. Попробуйте рассказать, что это за свойство. Проверьте, выполняется ли оно для квадратов нескольких следующих чисел, | + | 673. Попробуйте рассказать, что это за свойство. Проверьте, выполняется ли оно для квадратов нескольких следующих чисел. |
| | | | |
| - | <br>[[Image:16-06-5.jpg]]
| + | Первые единицы длины как в России, так и в других странах были связаны с размерами частей тела человека. Таковы сажень, локоть, пядь. В Англии и США до сих пор используется «ступня» — фут (31 см), «большой палеи,» — дюйм (25 мм) и даже ярд (91 см) — единица длины, появившаяся почти 900 лет назад. |
| | | | |
| - | <br>Первые единицы длины как в России, так и в других странах были связаны с размерами частей тела человека. Таковы '''''сажень, локоть, пядь'''''. В Англии и США до сих пор используется «ступня» — '''''фут''''' (31 см), «большой палеи,» — '''''дюйм''''' (25 мм) и даже '''''ярд''''' (91 см) — единица длины, появившаяся почти 900 лет назад. <br>Она была равна расстоянию от кончика носа короля Генриха I до конца пальцев его вытянутой руки. <br>Для измерения больших расстояний на Руси использовали единииу '''''пoприще''''', замененную позже верстбй (в разных местностях версту считали по-разному — от 500 до 750 сажен). <br>От восточных купцов пошла единица '''''аршин''''' (тоже означает «локоть») — существовали турецкий аршин, персидский аршин и др. Поэтому и возникла по- <br>говорка «мерить на свой аршин». <br>Множество единиц существовало и для измерения массы. Наиболее древняя русская мера — '''''гривна''''', или гривенка (около 410 г). Позднее появились золотники, фунты, пуды. <br>В связи с развитием торговли назрела необходимость установить четкие определения единиц и соотношения между ними. При Петре I русские меры были <br>приведены в определенную систему:
| + | Она была равна расстоянию от кончика носа короля Генриха I до конца пальцев его вытянутой руки. |
| | | | |
| - | 1 верста = 500 саженям (1 км 67 м); <br>1 сажень = 3 аршинам (2131см); <br>1 аршин = 16 вершкам = 28 дюймам (71 см); <br>1 фут = 12 дюймам (30 см 5 мм): <br>1 пуд = 40 фунтам (гривенкам) (16 кг 400 г); <br>1 фунт = 96 золотникам (410 г). <br><br> | + | Для измерения больших расстояний на Руси использовали единииу пoприще, замененную позже верстбй (в разных местностях версту считали по-разному — от 500 до 750 сажен). <br>От восточных купцов пошла единица '''''аршин''''' (тоже означает «локоть») — существовали турецкий аршин, персидский аршин и др. Поэтому и возникла по- <br>говорка «мерить на свой аршин». <br>Множество единиц существовало и для измерения массы. Наиболее древняя русская мера — [http://xvatit.com/busines/ '''гривна'''], или гривенка (около 410 г). Позднее появились золотники, фунты, пуды. |
| | + | |
| | + | В связи с развитием торговли назрела необходимость установить четкие определения единиц и соотношения между ними. При Петре I русские меры были приведены в определенную систему: |
| | + | |
| | + | 1 верста = 500 саженям (1 км 67 м); <br>1 сажень = 3 аршинам (2131см); <br>1 аршин = 16 вершкам = 28 дюймам (71 см); <br>1 фут = 12 дюймам (30 см 5 мм): <br>1 пуд = 40 фунтам (гривенкам) (16 кг 400 г); <br>1 фунт = 96 золотникам (410 г). <br> |
| | | | |
| | <br> ''Н.Я. ВИЛЕНКИН, B. И. ЖОХОВ, А. С. ЧЕСНОКОВ, C. И. ШВАРЦБУРД, Математика 5 класс, Учебник для общеобразовательных учреждений'' <br> | | <br> ''Н.Я. ВИЛЕНКИН, B. И. ЖОХОВ, А. С. ЧЕСНОКОВ, C. И. ШВАРЦБУРД, Математика 5 класс, Учебник для общеобразовательных учреждений'' <br> |
| | + | |
| | + | |
| | | | |
| | <sub>Книги и учебники согласно календарному плануванння по математике 5 класса [[Математика|скачать]], помощь школьнику [[Гипермаркет знаний - первый в мире!|онлайн]]</sub> | | <sub>Книги и учебники согласно календарному плануванння по математике 5 класса [[Математика|скачать]], помощь школьнику [[Гипермаркет знаний - первый в мире!|онлайн]]</sub> |
| Строка 138: |
Строка 161: |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | '''<u></u>''' | | '''<u></u>''' |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Произведение, в котором все множители равны друг другу, тоже записывают короче: вместо 2 • 2 • 2 • 2 • 2 • 2 пишут 26. Запись 26 читают: «два в шестой степени». В этой записи число 2 называют основанием степени, число 6, которое показывает, сколько множителей было в произведении, — показателем степени, а выражение 26 называют степенью.
торую степень числа часто называют иначе. Произведение 3 • 3 называют квадратом числа 3 и обозначают З2.
Произведение n и n называют квадратом числа n и обозначают n2 (читают: «эн в квадрате»). Итак, n2 = n • n.
Например, 172 = 17 • 17 = 289.
Третья степень числа также имеет и иное название. Произведение 4 • 4 • 4 называют кубом числа 4 и обозначают 43. Произведение n • n • n называют кубом числа n и обозначают n3 (читают: 5 «эн в кубе»).
Показатель степени 1 обычно не пишут.
Если в числовое выражение входят степени чисел, то их значения вычисляют до выполнения остальных действий.
Решение.
653. Представьте в виде степени произведение:
м) (7 - n)(7 - n).
655. Найдите значения: 252; 1002; 103; II3; 123; 153.
656. Найдите значения степеней: 25; 106; I20; З4; 411; 44.
657. Найдите значение выражения:
658. Пользуясь таблицами квадратов и кубов чисел, найдите значение д, если:
659. Вычислите устно:
661. Какие цифры заменены звездочками?
662. Каков порядок выполнения действий при вычислении значения выражения:
Если возможно, укажите другой порядок действий, приводящий к тому же результату.
663. Составьте выражение по следующей программе:
1. Разделить 58 344 на 429.
2. 215 умножить на 48.
3. Сложить результаты команд 1 и 2.
Найдите значение получившегося выражения.
664. Составьте схему вычисления выражения:
(39 • 71 + 25 • 95) - (248 : 4 - 176 : 11).
665. Решите задачу:
1) Сумма двух чисел 549. Одно из них в 8 раз больше другого. Найдите эти числа.
2) Сумма двух чисел 378. Одно из них в 8 раз меньше другого. Найдите эти числа.
3) Разность двух чисел 342. Одно из них в 7 раз меньше другого. Найдите эти числа.
4) Разность двух чисел 516. Одно из них в 7 раз больше другого. Найдите эти числа.
666. Найдите значения:
667. Найдите значения: 24; З3; 105; 112; 1004; 206.
668. Найдите значение выражения:
669. Из Москвы и Ростова-на-Дону одновременно вышли навстречу друг другу два поезда. Поезд из Москвы шел со скоростью 65 км/ч, а поезд из Ростова-на-Дону — со скоростью на 7 км/ч меньшей. На каком расстоянии друг от друга будут поезда через 6 ч после начала движения, если расстояние между Москвой и Ростовом-на-Дону 1230 км?
670. С двух станций, расстояние между которыми 720 км, вышли одновременно навстречу друг другу два поезда. Скорость первого поезда 75 км/ч, а скорость второго на 10 км/ч больше. На каком расстоянии друг от друга будут поезда через 4 ч?
671. Составьте программу вычислений для нахождения значения выражения
672. Выполните действия:
14 • (3600 • 18 - 239 200 : 46).
673. Попробуйте рассказать, что это за свойство. Проверьте, выполняется ли оно для квадратов нескольких следующих чисел.
Первые единицы длины как в России, так и в других странах были связаны с размерами частей тела человека. Таковы сажень, локоть, пядь. В Англии и США до сих пор используется «ступня» — фут (31 см), «большой палеи,» — дюйм (25 мм) и даже ярд (91 см) — единица длины, появившаяся почти 900 лет назад.
Она была равна расстоянию от кончика носа короля Генриха I до конца пальцев его вытянутой руки.
Для измерения больших расстояний на Руси использовали единииу пoприще, замененную позже верстбй (в разных местностях версту считали по-разному — от 500 до 750 сажен).
От восточных купцов пошла единица аршин (тоже означает «локоть») — существовали турецкий аршин, персидский аршин и др. Поэтому и возникла по-
говорка «мерить на свой аршин».
Множество единиц существовало и для измерения массы. Наиболее древняя русская мера — гривна, или гривенка (около 410 г). Позднее появились золотники, фунты, пуды.
В связи с развитием торговли назрела необходимость установить четкие определения единиц и соотношения между ними. При Петре I русские меры были приведены в определенную систему:
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.