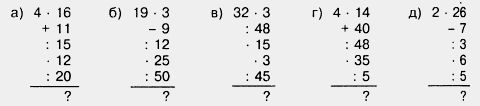|
|
|
| Строка 5: |
Строка 5: |
| | <br> | | <br> |
| | | | |
| - | ''' Объемы. Объем прямоугольного параллелепипеда ''' | + | '''Объемы. Объем прямоугольного параллелепипеда ''' |
| | | | |
| - | <br>Чтобы сравнить объемы двух сосудов, можно наполнить один из них водой и перелить ее во второй сосуд. Если второй сосуд окажется заполненным, а воды в первом сосуде не останется, то объемы сосудов равны. Если в первом сосуде вода останется, то его объем болыш объема второго сосуда. <br>А если заполнить водой второй сосуд не удастся, то объем первого сосуда меньше объема второго. <br>Если наполнить формочку влажным песком, а потом перевернуть и снять ее, получится фигура, имеющая тот же объем, что и формочка (рис. 83). | + | <br>Чтобы сравнить объемы двух сосудов, можно наполнить один из них водой и перелить ее во второй сосуд. Если второй сосуд окажется заполненным, а воды в первом сосуде не останется, то объемы сосудов равны. Если в первом сосуде вода останется, то его объем болыш объема второго сосуда. <br> |
| | | | |
| - | [[Image:16-06-33.jpg]]<br><br>Для измерения объемов применяют следующие единицы: '''кубический миллиметр (мм3), кубический сантиметр (см3), кубический дециметр (дм<sup>3</sup>), кубический метр (м<sup>3</sup>), кубический километр (км<sup>3</sup>). '''<br>Например: кубический сантиметр — это объем куба с ребром 1 см (рис. 84). <br>Кубический дециметр называют также литром. <br>''' 1 л = 1 дм3 '''<br>Фигура на рисунке 85 состоит из 4 кубиков с ребром 1 см. Значит, ее объем равен 4 см<sup>3</sup>. <br>Выведем правило для вычисления объема прямоугольного параллелепипеда. Пусть прямоугольный параллелепипед имеет длину 4 см, ширину 3 см и высоту 2 см (рис. 86, а). Разобьем его на два слоя толщиной 1 см
| + | А если заполнить водой второй сосуд не удастся, то объем первого сосуда меньше объема второго. <br> |
| | | | |
| - | [[Image:16-06-34.jpg]]<br>
| + | Если наполнить формочку влажным песком, а потом перевернуть и снять ее, получится фигура, имеющая тот же объем, что и формочка (рис. 83). |
| | | | |
| | + | [[Image:16-06-33.jpg|480px|Объемы]]<br><br>Для измерения объемов применяют следующие единицы: кубический миллиметр (мм3), кубический сантиметр (см3), кубический дециметр (дм<sup>3</sup>), кубический метр (м<sup>3</sup>), кубический километр (км<sup>3</sup>). <br> |
| | | | |
| | + | Например: кубический сантиметр — это объем куба с ребром 1 см (рис. 84). <br> |
| | | | |
| - | [[Image:16-06-35.jpg]]<br>(рис. 86, б). Каждый из этих слоев состоит из 3 столбиков длиной 4 см (рис. 86, s), а каждый столбик — из 4 кубиков с ребром 1 см (рис. 86, г). <br>Значит, объем каждого столбика равен 4 см3, каждого слоя — 4 • 3 ( см<sup>3</sup>), а всего прямоугольного параллелепипеда — (4 • 3) • 2, то есть 24 см<sup>3</sup>.
| + | Кубический дециметр называют также литром. <br> |
| | | | |
| - | '''''Чтобы найти объем прямоугольного параллелепипеда, надо его длину умножить на ширину и на высоту.''''' | + | '''1 л = 1 дм'''<sup>'''3'''</sup><br> |
| | + | |
| | + | Фигура на рисунке 85 состоит из 4 кубиков с ребром 1 см. Значит, ее объем равен 4 см<sup>3</sup>. <br> |
| | + | |
| | + | Выведем правило для вычисления объема прямоугольного параллелепипеда. Пусть прямоугольный параллелепипед имеет длину 4 см, ширину 3 см и высоту 2 см (рис. 86, а). Разобьем его на два слоя толщиной 1 см |
| | + | |
| | + | [[Image:16-06-34.jpg|480px|Объемы]]<br> |
| | + | |
| | + | <br> |
| | + | |
| | + | [[Image:16-06-35.jpg|480px|Объемы]]<br>(рис. 86, б). Каждый из этих слоев состоит из 3 столбиков длиной 4 см (рис. 86, s), а каждый столбик — из 4 кубиков с ребром 1 см (рис. 86, г). <br> |
| | + | |
| | + | Значит, объем каждого столбика равен 4 см3, каждого слоя — 4 • 3 ( см<sup>3</sup>), а всего прямоугольного параллелепипеда — (4 • 3) • 2, то есть 24 см<sup>3</sup>. |
| | + | |
| | + | ''Чтобы найти объем прямоугольного параллелепипеда, надо его длину умножить на ширину и на высоту.'' |
| | | | |
| | Формула объема прямоугольного параллелепипеда имеет вид | | Формула объема прямоугольного параллелепипеда имеет вид |
| | | | |
| - | '''V = abc, '''<br>где V — объем; а, b, с — измерения.
| + | '''V = abc, '''<br>где V — объем; а, b, с — измерения. |
| | | | |
| - | Если ребро куба равно 4 см, то объем куба равен 4 • 4 • 4 = 43 (см<sup>3</sup>), то есть 64 см<sup>3</sup>. <br>Если ребро куба равно а, то объем V куба равен a • a • a = a<sup>3</sup> | + | Если ребро куба равно 4 см, то объем куба равен 4 • 4 • 4 = 43 (см<sup>3</sup>), то есть 64 см<sup>3</sup>. |
| | | | |
| - | Значит, формула объема куба имеет вид <br>''' V = a<sup>3</sup>'''<br>Именно поэтому запись а<sup>3</sup> называют кубом числа а. <br>Объем куба с ребром 1 м равен 1 м<sup>3</sup>. А так как 1 м = 10 дм, то 1 м<sup>3</sup> = 103 дм<sup>3</sup>, то есть 1 м<sup>3</sup> = 1000 дм<sup>3</sup> = 1000 л. <br>Таким же образом находим, что | + | Если ребро куба равно а, то объем V куба равен a • a • a = a<sup>3</sup> |
| | + | |
| | + | Значит, формула объема куба имеет вид <br> |
| | + | |
| | + | '''V = a<sup>3</sup>''' |
| | + | |
| | + | Именно поэтому запись а<sup>3</sup> называют кубом числа а. |
| | + | |
| | + | Объем куба с ребром 1 м равен 1 м<sup>3</sup>. А так как 1 м = 10 дм, то 1 м<sup>3</sup> = 103 дм<sup>3</sup>, то есть 1 м<sup>3</sup> = 1000 дм<sup>3</sup> = 1000 л. <br>Таким же образом находим, что |
| | | | |
| | 1 л = 1 дм3 = 1000 см<sup>3</sup>; 1 см3 = 1000 мм<sup>3</sup>; <br>1 км<sup>3</sup> = 1 000 000 000 м<sup>3</sup> (см. форзац). | | 1 л = 1 дм3 = 1000 см<sup>3</sup>; 1 см3 = 1000 мм<sup>3</sup>; <br>1 км<sup>3</sup> = 1 000 000 000 м<sup>3</sup> (см. форзац). |
| | | | |
| - | '''Фигура состоит из 19 кубиков со стороной 1*см каждый; чему равен объем этой фигуры? <br>Что такое кубический сантиметр; кубический метр? <br>Как еще называют кубический дециметр? <br>Скольким кубическим сантиметрам равен 1 литр? <br>Скольким литрам равен кубический метр? <br>Сколько кубических метров в кубическом километре? <br>Напишите формулу объема прямоугольного параллелепипеда. <br>Что означает в этой формуле буква V; буквы а, b, с? <br>Напишите формулу объема куба.'''
| |
| | | | |
| | + | ''Фигура состоит из 19 кубиков со стороной 1*см каждый; чему равен объем этой фигуры? <br>Что такое кубический сантиметр; кубический метр? <br>Как еще называют кубический дециметр? <br>Скольким кубическим сантиметрам равен 1 литр? <br>Скольким литрам равен кубический метр? <br>Сколько кубических метров в кубическом километре? <br>Напишите формулу объема прямоугольного параллелепипеда. <br>Что означает в этой формуле буква V; буквы а, b, с? <br>Напишите формулу объема куба.'' |
| | | | |
| | + | <br> |
| | | | |
| - | [[Image:16-06-36.jpg]] | + | [[Image:16-06-36.jpg|550px|Объемы]] |
| | | | |
| | <br>819. Из кубиков с ребром 1 см составлены фигуры (рис. 87). Найдите объемы и площади поверхностей этих фигур. | | <br>819. Из кубиков с ребром 1 см составлены фигуры (рис. 87). Найдите объемы и площади поверхностей этих фигур. |
| Строка 57: |
Строка 82: |
| | 828. Прямоугольный параллелепипед (рис. 88) разделен на две части Найдите объем и площадь поверхности всего параллелепипеда и обеих его частей. Равен ли объем параллелепипеда сумме объемов его частей? Можна ли это сказать о площадях их поверхностей? Объясните почему. | | 828. Прямоугольный параллелепипед (рис. 88) разделен на две части Найдите объем и площадь поверхности всего параллелепипеда и обеих его частей. Равен ли объем параллелепипеда сумме объемов его частей? Можна ли это сказать о площадях их поверхностей? Объясните почему. |
| | | | |
| - | [[Image:16-06-37.jpg]]<br><br>829. Вычислите устно: | + | [[Image:16-06-37.jpg|550px|Объемы]]<br><br>829. Вычислите устно: |
| | | | |
| - | [[Image:16-06-38.jpg]]<br><br>830. Восстановите цепочку вычислений: | + | [[Image:16-06-38.jpg|480px|Задание]]<br><br>830. Восстановите цепочку вычислений: |
| | | | |
| - | [[Image:16-06-39.jpg]]<br><br>831. Найдите значение выражения: | + | [[Image:16-06-39.jpg|480px|Задание]]<br><br>831. Найдите значение выражения: |
| | | | |
| | а)2<sup>3</sup> + 3<sup>2</sup>; б)3<sup>3</sup> + 5<sup>2</sup>; | | а)2<sup>3</sup> + 3<sup>2</sup>; б)3<sup>3</sup> + 5<sup>2</sup>; |
| Строка 69: |
Строка 94: |
| | 832. Сколько десятков получится в частном: | | 832. Сколько десятков получится в частном: |
| | | | |
| - | а) 1652 : 7; в) 1632 : 12; <br>б) 774 : 6; г) 2105 : 5? <br><br>833. Согласны ли вы с утверждением: | + | а) 1652 : 7; в) 1632 : 12; <br>б) 774 : 6; г) 2105 : 5? <br><br>833. Согласны ли вы с утверждением: |
| | | | |
| | а) любой куб является и прямоугольным параллелепипедом; <br>б) если длина прямоугольного параллелепипеда не равна его высоте, то он не может быть кубом; <br>в) каждая грань куба — квадрат? | | а) любой куб является и прямоугольным параллелепипедом; <br>б) если длина прямоугольного параллелепипеда не равна его высоте, то он не может быть кубом; <br>в) каждая грань куба — квадрат? |
| Строка 81: |
Строка 106: |
| | а) две грани, имеющие общее ребро; <br>б) верхнюю, заднюю, переднюю и нижнюю грани; <br>в) вертикальные ребра. | | а) две грани, имеющие общее ребро; <br>б) верхнюю, заднюю, переднюю и нижнюю грани; <br>в) вертикальные ребра. |
| | | | |
| - | [[Image:16-06-40.jpg]] | + | [[Image:16-06-40.jpg|180px|Задание]] |
| | | | |
| | <br>837. Решите задачу: | | <br>837. Решите задачу: |
| | | | |
| - | 1) Найдите площадь каждого участка, если площадь первого участка в 5 раз больше площади второго, а площадь второго на 252 га меньше площади первого. <br>2) Найдите площадь каждого участка, если площадь второго участка на 324 га больше площади первого участка, а площадь первого участка в 7 раз меньше <br>площади второго. | + | 1) Найдите площадь каждого участка, если площадь первого участка в 5 раз больше площади второго, а площадь второго на 252 га меньше площади первого. |
| | + | |
| | + | 2) Найдите площадь каждого участка, если площадь второго участка на 324 га больше площади первого участка, а площадь первого участка в 7 раз меньше площади второго. |
| | | | |
| | 838. Выполните действия: | | 838. Выполните действия: |
| | | | |
| - | 1) 668 • (3076 + 5081); <br>2)783 • (66 161 - 65 752); <br>3) 2 111 022 : (5960 - 5646); <br>4) 2 045 639 : (6700 - 6279). | + | 1) 668 • (3076 + 5081); <br>2)783 • (66 161 - 65 752); <br>3) 2 111 022 : (5960 - 5646); <br>4) 2 045 639 : (6700 - 6279). |
| | | | |
| - | 839. На Русы в старину использовались в качестве единиц измерения объема ведрб (около 12 л), штоф {десятая часть ведра). В США, Англии и других стра- <br>нах используются бйррель {около 159 л), галлбн (около 4 л), бушель {около 36 л), пинта (от 470 до 568 кубических сантиметров). Сравните эти единицы, какие из них больше 1 м3? | + | 839. На Русы в старину использовались в качестве единиц измерения объема ведрб (около 12 л), штоф {десятая часть ведра). В США, Англии и других странах используются бйррель {около 159 л), галлбн (около 4 л), бушель {около 36 л), пинта (от 470 до 568 кубических сантиметров). Сравните эти единицы, какие из них больше 1 м<sup>3</sup>? |
| | | | |
| - | [[Image:16-06-41.jpg]]
| + | 840. Найдите объемы фигур, изображенных на рисунке 90. Объем каждого кубика равен 1 см<sup>3</sup>. |
| - | | + | |
| - | <br>840. Найдите объемы фигур, изображенных на рисунке 90. Объем каждого кубика равен 1 см<sup>3</sup>.
| + | |
| | | | |
| | 841. Найдите объем прямоугольного параллелепипеда (рис. 91). | | 841. Найдите объем прямоугольного параллелепипеда (рис. 91). |
| Строка 101: |
Строка 126: |
| | 842. Найдите объем прямоугольного параллелепипеда, если его измерения — 48 дм, 16 дм и 12 дм. | | 842. Найдите объем прямоугольного параллелепипеда, если его измерения — 48 дм, 16 дм и 12 дм. |
| | | | |
| - | 843. Сарай, имеющий форму прямоугольного параллелепипеда, заполнен сеном. Длина сарая 10 м, ширина 6 м, высота 4 м. Найдите массу сена в сарае, если масса 10 м3 сена равна 6 ц. | + | 843. Сарай, имеющий форму прямоугольного параллелепипеда, заполнен сеном. Длина сарая 10 м, ширина 6 м, высота 4 м. Найдите массу сена в сарае, если масса 10 м<sup>3</sup> сена равна 6 ц. |
| | | | |
| - | [[Image:16-06-42.jpg]] | + | [[Image:16-06-42.jpg|480px|Задание]] |
| | | | |
| | + | <br> |
| | | | |
| - | | + | [[Image:16-06-43.jpg|240px|Задание]]<br><br>844. Выразите в кубических дециметрах: |
| - | [[Image:16-06-43.jpg]]<br><br>844. Выразите в кубических дециметрах: | + | |
| | | | |
| | 2 м<sup>3</sup> 350 дм<sup>3</sup>; 18 000 см<sup>3</sup>; <br>3 м<sup>3</sup> 7 дм<sup>3</sup>; 210 000 см<sup>3</sup>. <br>4 м<sup>3</sup> 30 дм<sup>3</sup>; | | 2 м<sup>3</sup> 350 дм<sup>3</sup>; 18 000 см<sup>3</sup>; <br>3 м<sup>3</sup> 7 дм<sup>3</sup>; 210 000 см<sup>3</sup>. <br>4 м<sup>3</sup> 30 дм<sup>3</sup>; |
| Строка 125: |
Строка 150: |
| | 848. Найдите значение выражения: | | 848. Найдите значение выражения: |
| | | | |
| - | а) 700 700 - 6054 • (47 923 - 47 884) - 65 548; <br>б) 66 509 + 141 400 : (39 839 - 39 739) + 1985; <br>в) (851 + 2331) : 74 - 34; <br>г) (14 084 : 28 - 23) -27-12 060; <br>д) (102 + II2 + 122) : 73 + 895; <br>е) 2555 : (132 + 142) + 35. <br><br>849. Подсчитайте по таблице (рис. 92): <br>а) сколько раз встречается цифра 9; <br>б) сколько раз всего в таблице встречаются цифры 6 и 7 (не считая их по отдельности); <br>в) сколько раз всего встречаются цифры 5, б и 8 (не считая их по отдельности). | + | а) 700 700 - 6054 • (47 923 - 47 884) - 65 548; <br>б) 66 509 + 141 400 : (39 839 - 39 739) + 1985; <br>в) (851 + 2331) : 74 - 34; <br>г) (14 084 : 28 - 23) -27-12 060; <br>д) (102 + II2 + 122) : 73 + 895; <br>е) 2555 : (132 + 142) + 35. <br><br>849. Подсчитайте по таблице (рис. 92): |
| | | | |
| | + | а) сколько раз встречается цифра 9; <br>б) сколько раз всего в таблице встречаются цифры 6 и 7 (не считая их по отдельности); <br>в) сколько раз всего встречаются цифры 5, б и 8 (не считая их по отдельности). |
| | | | |
| | + | <br> |
| | | | |
| - | [[Image:16-06-44.jpg]]<br><br>[[Image:16-06-45.jpg]] | + | [[Image:16-06-44.jpg|320px|Задание]]<br><br>[[Image:16-06-45.jpg|550px|Правила]]<br> |
| | | | |
| | + | 200 лет назад в разных странах, в том числе и в России, применялись различные системы единиц для измерения длины, массы и других величин. Соотношения между мерами были сложны, существовали разные определения для единиц измерения. Например, и до сих пор в Великобритании существуют две различные «тонны» (в 2000 и в 2940 фунтов), более 50 различных «бушелей» и т. п. Это затрудняло развитие науки, торговли между странами. Поэтому назрела необходимость введения единой системы мер, удобной для всех стран, с простыми соотношениями между единицами. |
| | | | |
| | + | Такая система — ее назвали метрической системой мер — была разработана во Франции. Основную единииу длины, 1 метр (от греческого слова «метрон» — мера), определили как сорокамиллионную долю окружности Земли, основную единицу массы, 1 килограмм — как массу 1 дм<sup>3</sup> чистой воды. Остальные единицы определялись через эти две, соотношения между единицами одной величины равнялись 10, 100, 1000 и т. д. |
| | | | |
| - | [[Image:16-06-46.jpg]] | + | Метрическая система мер принята большинством стран мира, в России ее введение началось с 1899 года. Большие заслуги во введении и распространении метрической системы мер в нашей стране принадлежат Дмитрию Ивановичу Менделееву, великому русскому [http://xvatit.com/vuzi/ '''химику''']. |
| | | | |
| - | <br>200 лет назад в разных странах, в том числе и в России, применялись различные системы единиц для измерения длины, массы и других величин. Соотношения между мерами были сложны, существовали разные определения для единиц измерения. Например, и до сих пор в Великобритании существуют две различные «тонны» (в 2000 и в 2940 фунтов), более 50 различных «бушелей» и т. п. Это затрудняло развитие науки, торговли между странами. Поэтому назрела необходимость введения единой системы мер, удобной для всех стран, с простыми соотношениями между единицами.
| + | Однако по традиции и в настоящее время иногда пользуются старыми единицами. Моряки измеряют расстояния милями (1852 м) и кабельтовыми (десятая часть мили, то есть около 185 м), скорость — узлйми (1 миля в час). Массу алмазов измеряют в карйтах (200 мг, то есть пятая часть грамма -— масса пшеничного зерна). Объем нефти измеряют в бйррелях (159 л) и т. д. <br> |
| | | | |
| - | Такая система — ее назвали метрической системой мер — была разработана во Франции. Основную единииу длины, 1 метр (от греческого слова «метрон» — <br>мера), определили как сорокамиллионную долю окружности Земли, основную единицу массы, 1 килограмм — как массу 1 дм3 чистой воды. Остальные единицы определялись через эти две, соотношения между единицами одной величины равнялись 10, 100, 1000 и т. д.
| + | <br> ''Н.Я. ВИЛЕНКИН, B. И. ЖОХОВ, А. С. ЧЕСНОКОВ, C. И. ШВАРЦБУРД, Математика 5 класс, Учебник для общеобразовательных учреждений'' <br> |
| | | | |
| - | Метрическая система мер принята большинством стран мира, в России ее введение началось с 1899 года. Большие заслуги во введении и распространении <br>метрической системы мер в нашей стране принадлежат Дмитрию Ивановичу Менделееву, великому русскому химику.
| |
| | | | |
| - | Однако по традиции и в настоящее время иногда пользуются старыми единицами. Моряки измеряют расстояния милями (1852 м) и кабельтовыми (десятая часть мили, то есть около 185 м), скорость — узлйми (1 миля в час). Массу алмазов измеряют в карйтах (200 мг, то есть пятая часть грамма -— масса <br>пшеничного зерна). Объем нефти измеряют в бйррелях (159 л) и т. д. <br>
| |
| - |
| |
| - | <br> ''Н.Я. ВИЛЕНКИН, B. И. ЖОХОВ, А. С. ЧЕСНОКОВ, C. И. ШВАРЦБУРД, Математика 5 класс, Учебник для общеобразовательных учреждений'' <br>
| |
| | | | |
| | <sub>Книги, учебники математике [[Математика|скачать]], конспект на помощь учителю и ученикам, учиться [[Гипермаркет знаний - первый в мире!|онлайн]]</sub> | | <sub>Книги, учебники математике [[Математика|скачать]], конспект на помощь учителю и ученикам, учиться [[Гипермаркет знаний - первый в мире!|онлайн]]</sub> |
| Строка 150: |
Строка 175: |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | '''<u></u>''' | | '''<u></u>''' |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Версия 07:58, 5 октября 2012
Гипермаркет знаний>>Математика>>Математика 5 класс>>Математика:Объемы. Объем прямоугольного параллелепипеда
Объемы. Объем прямоугольного параллелепипеда
Чтобы сравнить объемы двух сосудов, можно наполнить один из них водой и перелить ее во второй сосуд. Если второй сосуд окажется заполненным, а воды в первом сосуде не останется, то объемы сосудов равны. Если в первом сосуде вода останется, то его объем болыш объема второго сосуда.
А если заполнить водой второй сосуд не удастся, то объем первого сосуда меньше объема второго.
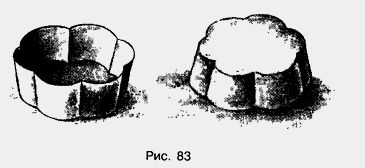
Если наполнить формочку влажным песком, а потом перевернуть и снять ее, получится фигура, имеющая тот же объем, что и формочка (рис. 83).
Для измерения объемов применяют следующие единицы: кубический миллиметр (мм3), кубический сантиметр (см3), кубический дециметр (дм3), кубический метр (м3), кубический километр (км3).
Например: кубический сантиметр — это объем куба с ребром 1 см (рис. 84).
Кубический дециметр называют также литром.
1 л = 1 дм3
Фигура на рисунке 85 состоит из 4 кубиков с ребром 1 см. Значит, ее объем равен 4 см3.
Выведем правило для вычисления объема прямоугольного параллелепипеда. Пусть прямоугольный параллелепипед имеет длину 4 см, ширину 3 см и высоту 2 см (рис. 86, а). Разобьем его на два слоя толщиной 1 см
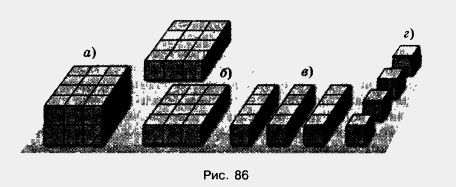
(рис. 86, б). Каждый из этих слоев состоит из 3 столбиков длиной 4 см (рис. 86, s), а каждый столбик — из 4 кубиков с ребром 1 см (рис. 86, г).
Значит, объем каждого столбика равен 4 см3, каждого слоя — 4 • 3 ( см3), а всего прямоугольного параллелепипеда — (4 • 3) • 2, то есть 24 см3.
Чтобы найти объем прямоугольного параллелепипеда, надо его длину умножить на ширину и на высоту.
Формула объема прямоугольного параллелепипеда имеет вид
V = abc,
где V — объем; а, b, с — измерения.
Если ребро куба равно 4 см, то объем куба равен 4 • 4 • 4 = 43 (см3), то есть 64 см3.
Если ребро куба равно а, то объем V куба равен a • a • a = a3
Значит, формула объема куба имеет вид
V = a3
Именно поэтому запись а3 называют кубом числа а.
Объем куба с ребром 1 м равен 1 м3. А так как 1 м = 10 дм, то 1 м3 = 103 дм3, то есть 1 м3 = 1000 дм3 = 1000 л.
Таким же образом находим, что
1 л = 1 дм3 = 1000 см3; 1 см3 = 1000 мм3;
1 км3 = 1 000 000 000 м3 (см. форзац).
Фигура состоит из 19 кубиков со стороной 1*см каждый; чему равен объем этой фигуры?
Что такое кубический сантиметр; кубический метр?
Как еще называют кубический дециметр?
Скольким кубическим сантиметрам равен 1 литр?
Скольким литрам равен кубический метр?
Сколько кубических метров в кубическом километре?
Напишите формулу объема прямоугольного параллелепипеда.
Что означает в этой формуле буква V; буквы а, b, с?
Напишите формулу объема куба.
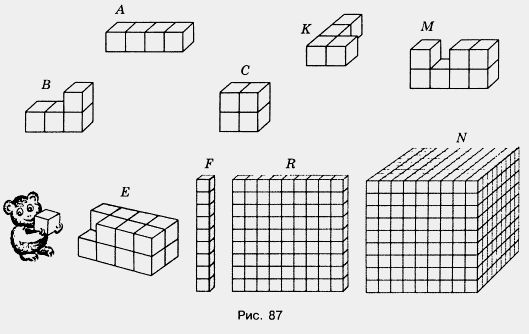
819. Из кубиков с ребром 1 см составлены фигуры (рис. 87). Найдите объемы и площади поверхностей этих фигур.
820. Найдите объем прямоугольного параллелепипеда, если
а) а = 6 см, b = 10 см, с = 5 см;
б) а = 30 дм, b = 20 дм, с = 30 дм;
в) а = 8 дм, b = 6 м, с = 12 м;
г) а = 2 дм 1 см, b = 1 дм 7 см, с = 8 см;
д) а = 3 м, b = 2 дм, с = 15 см.
821. Площадь нижней грани прямоугольного параллелепипеда равна 24 см2. Определите высоту этого параллелепипеда, если его объем равен 96 см3.
822. Объем комнаты равен 60 м3. Высота комнаты 3 м, ширина 4 м. Найдите длину комнаты и площади пола, потолка, стен.
823. Найдите объем куба, ребро которого 8 дм; 3 дм 6 см.
824. Найдите объем куба, если площадь его поверхности равна 96 см2.
825. Выразите:
а) в кубических сантиметрах: 5 дм3 635 см3; 2 дм3 80 см3;
б) в кубических дециметрах: 6 м3 580 дм3; 7 м3 15 дм3;
в) в кубических метрах и дециметрах: 3270 дм3; 12 540 000 см3.
826. Высота комнаты 3 м, ширина 5 м и длина 6 м. Сколько кубических метров воздуха находится в комнате?
827. Длина аквариума 80 см, ширина 45 см, а высота 55 см. Сколько литров воды надо влить в этот аквариум, чтобы уровень воды был ниже верхнего края аквариума на 10 см?
828. Прямоугольный параллелепипед (рис. 88) разделен на две части Найдите объем и площадь поверхности всего параллелепипеда и обеих его частей. Равен ли объем параллелепипеда сумме объемов его частей? Можна ли это сказать о площадях их поверхностей? Объясните почему.
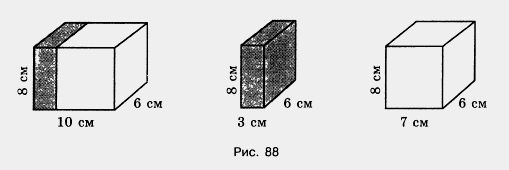
829. Вычислите устно:
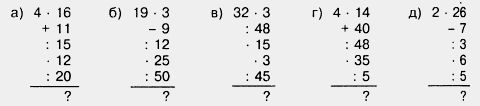
830. Восстановите цепочку вычислений:
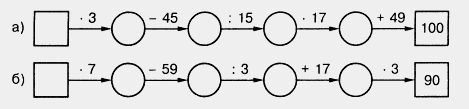
831. Найдите значение выражения:
а)23 + 32; б)33 + 52;
в) 43 + 6; г) 103 - 10.
832. Сколько десятков получится в частном:
а) 1652 : 7; в) 1632 : 12;
б) 774 : 6; г) 2105 : 5?
833. Согласны ли вы с утверждением:
а) любой куб является и прямоугольным параллелепипедом;
б) если длина прямоугольного параллелепипеда не равна его высоте, то он не может быть кубом;
в) каждая грань куба — квадрат?
834. Четыре одинаковые бочки вмещают 26 ведер воды. Сколько ведер воды могут вместить 10 таких бочек?
835. Сколькими способами из 7 бусинок разных цветов можно составить ожерелье (с застежкой)?
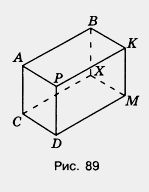
836. Назовите в прямоугольном параллелепипеде (рис. 89):
а) две грани, имеющие общее ребро;
б) верхнюю, заднюю, переднюю и нижнюю грани;
в) вертикальные ребра.
837. Решите задачу:
1) Найдите площадь каждого участка, если площадь первого участка в 5 раз больше площади второго, а площадь второго на 252 га меньше площади первого.
2) Найдите площадь каждого участка, если площадь второго участка на 324 га больше площади первого участка, а площадь первого участка в 7 раз меньше площади второго.
838. Выполните действия:
1) 668 • (3076 + 5081);
2)783 • (66 161 - 65 752);
3) 2 111 022 : (5960 - 5646);
4) 2 045 639 : (6700 - 6279).
839. На Русы в старину использовались в качестве единиц измерения объема ведрб (около 12 л), штоф {десятая часть ведра). В США, Англии и других странах используются бйррель {около 159 л), галлбн (около 4 л), бушель {около 36 л), пинта (от 470 до 568 кубических сантиметров). Сравните эти единицы, какие из них больше 1 м3?
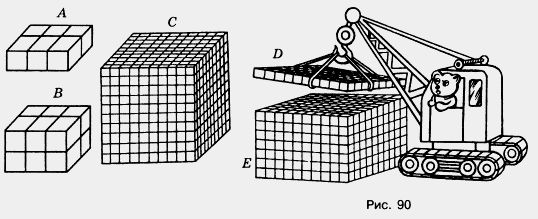
840. Найдите объемы фигур, изображенных на рисунке 90. Объем каждого кубика равен 1 см3.
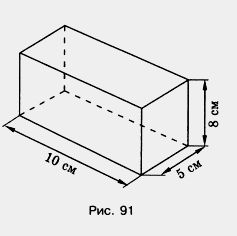
841. Найдите объем прямоугольного параллелепипеда (рис. 91).
842. Найдите объем прямоугольного параллелепипеда, если его измерения — 48 дм, 16 дм и 12 дм.
843. Сарай, имеющий форму прямоугольного параллелепипеда, заполнен сеном. Длина сарая 10 м, ширина 6 м, высота 4 м. Найдите массу сена в сарае, если масса 10 м3 сена равна 6 ц.
844. Выразите в кубических дециметрах:
2 м3 350 дм3; 18 000 см3;
3 м3 7 дм3; 210 000 см3.
4 м3 30 дм3;
845. Объем прямоугольного параллелепипеда 1248 см3. Его длина 13 см, а ширина 8 см. Найдите высоту этого параллелепипеда.
846. С помощью формулы V = abc вычислите:
а) V, если а = 3 дм, b = 4 дм, с = 5 дм;
б) а, если V = 2184 см3, b = 12 см, с =13 см;
в) b, если V = 9200 см3, а = 23 см, с = 25 см;
г) аЬ если V = 1088 дм3, с = 17 см.
Каков смысл произведения ab?
847. Отец старше сына на 21 год. Запишите формулу, выражающую а — возраст отца — через b — возраст сына. Найдите по этой формуле:
а) а, если b = 10; б) а, если b = 18; в) b, если а = 48.
848. Найдите значение выражения:
а) 700 700 - 6054 • (47 923 - 47 884) - 65 548;
б) 66 509 + 141 400 : (39 839 - 39 739) + 1985;
в) (851 + 2331) : 74 - 34;
г) (14 084 : 28 - 23) -27-12 060;
д) (102 + II2 + 122) : 73 + 895;
е) 2555 : (132 + 142) + 35.
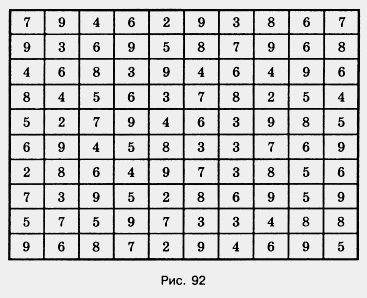
849. Подсчитайте по таблице (рис. 92):
а) сколько раз встречается цифра 9;
б) сколько раз всего в таблице встречаются цифры 6 и 7 (не считая их по отдельности);
в) сколько раз всего встречаются цифры 5, б и 8 (не считая их по отдельности).

200 лет назад в разных странах, в том числе и в России, применялись различные системы единиц для измерения длины, массы и других величин. Соотношения между мерами были сложны, существовали разные определения для единиц измерения. Например, и до сих пор в Великобритании существуют две различные «тонны» (в 2000 и в 2940 фунтов), более 50 различных «бушелей» и т. п. Это затрудняло развитие науки, торговли между странами. Поэтому назрела необходимость введения единой системы мер, удобной для всех стран, с простыми соотношениями между единицами.
Такая система — ее назвали метрической системой мер — была разработана во Франции. Основную единииу длины, 1 метр (от греческого слова «метрон» — мера), определили как сорокамиллионную долю окружности Земли, основную единицу массы, 1 килограмм — как массу 1 дм3 чистой воды. Остальные единицы определялись через эти две, соотношения между единицами одной величины равнялись 10, 100, 1000 и т. д.
Метрическая система мер принята большинством стран мира, в России ее введение началось с 1899 года. Большие заслуги во введении и распространении метрической системы мер в нашей стране принадлежат Дмитрию Ивановичу Менделееву, великому русскому химику.
Однако по традиции и в настоящее время иногда пользуются старыми единицами. Моряки измеряют расстояния милями (1852 м) и кабельтовыми (десятая часть мили, то есть около 185 м), скорость — узлйми (1 миля в час). Массу алмазов измеряют в карйтах (200 мг, то есть пятая часть грамма -— масса пшеничного зерна). Объем нефти измеряют в бйррелях (159 л) и т. д.
Н.Я. ВИЛЕНКИН, B. И. ЖОХОВ, А. С. ЧЕСНОКОВ, C. И. ШВАРЦБУРД, Математика 5 класс, Учебник для общеобразовательных учреждений
Книги, учебники математике скачать, конспект на помощь учителю и ученикам, учиться онлайн
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|