|
|
| Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Свойство диагоналей параллелограмма</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Свойство диагоналей параллелограмма, отрезок, прямая, Треугольники</metakeywords> |
| | | | |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика: Свойство диагоналей параллелограмма''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика: Свойство диагоналей параллелограмма''' |
| Строка 5: |
Строка 5: |
| | <br> | | <br> |
| | | | |
| - | '''СВОЙСТВО ДИАГОНАЛЕЙ ПАРАЛЛЕЛОГРАММА'''
| + | '''Свойство диагоналей параллелограмма''' |
| | | | |
| - | <br>Теорема 6.2 (обратная теореме 6.1).'''''Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.''''' | + | <br>Теорема 6.2 (обратная теореме 6.1). Диагонали '''[[Паралелограм. Ознаки паралелограма. Властивості паралелограма|параллелограмма]]''' пересекаются и точкой пересечения делятся пополам. |
| | | | |
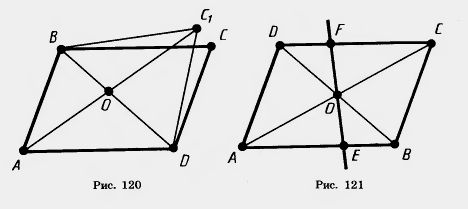
| - | Доказательство. Пусть ABCD — данный параллелограмм (рис. 120). Проведем его диагональ BD. Отметим на ней середину О и на продолжении отрезка АО отложим отрезок ОС<sub>1</sub>, равный АО. | + | Доказательство. Пусть ABCD — данный параллелограмм (рис. 120). Проведем его диагональ BD. Отметим на ней середину О и на продолжении отрезка АО отложим '''[[Отрезок. Полные уроки|отрезок]]''' ОС<sub>1</sub>, равный АО. |
| | | | |
| - | По теореме 6.1 четырехугольник ABC<sub>1</sub>D есть параллелограмм. Следовательно, прямая ВС<sub>1</sub> параллельна AD. Но через точку В можно провести только одну прямую, параллельную AD. Значит, прямая ВС<sub>1</sub> совпадает с прямой ВС. | + | По теореме 6.1 четырехугольник ABC<sub>1</sub>D есть параллелограмм. Следовательно, прямая ВС<sub>1</sub> параллельна AD. Но через точку В можно провести только одну прямую, параллельную AD. Значит, прямая ВС<sub>1</sub> совпадает с прямой ВС. |
| | | | |
| - | Точно так же доказывается, что прямая DC<sub>1</sub> совпадает с прямой DC. | + | Точно так же доказывается, что '''[[Точка и прямая|прямая]]''' DC<sub>1</sub> совпадает с прямой DC. |
| | | | |
| - | Значит, точка С<sub>1 </sub>совпадает с точкой С. Параллелограмм ABCD совпадает с ABC<sub>1</sub>D. Поэтому его диагонали пересекаются и точкой пересечения делятся пополам. Теорема доказана. | + | Значит, точка С<sub>1 </sub>совпадает с точкой С. Параллелограмм ABCD совпадает с ABC<sub>1</sub>D. Поэтому его диагонали пересекаются и точкой пересечения делятся пополам. Теорема доказана.<br> |
| | | | |
| | + | [[Image:22-06-4.jpg|480px|Свойство диагоналей параллелограмма]]<br>Задача (6). Через точку пересечения диагоналей параллелограмма проведена прямая. Докажите, что отрезок ее, заключенный между параллельными сторонами, делится этой точкой пополам. |
| | | | |
| | + | '''Решение'''. Пусть ABCD — данный параллелограмм и EF — прямая, пересекающая параллельные стороны АВ и CD (рис. 121). '''[[Треугольник. Полные уроки|Треугольники]]''' ОАЕ и ОСЕ равны по второму признаку. У них стороны OA и ОС равны, так как О — середина диагонали АС. Углы при вершине О равны как вертикальные, а углы ЕАО и FCO равны как внутренние накрест лежащие при параллельных АВ, CD и секущей АС. |
| | | | |
| - | [[Image:22-06-4.jpg]]<br><br><br>Задача (6). Через точку пересечения диагоналей параллелограмма проведена прямая. Докажите, что отрезок ее, заключенный между параллельными сторонами, делится этой точкой пополам.
| + | Из равенства треугольников следует равенство сторон: OE=OF, что и требовалось доказать. |
| | | | |
| - | Решение. Пусть ABCD — данный параллелограмм и EF — прямая, пересекающая параллельные стороны АВ и CD (рис. 121). Треугольники ОАЕ и ОСЕ равны по второму признаку. У них стороны OA и ОС равны, так как О — середина диагонали АС. Углы при вершине О равны как вертикальные, а углы ЕАО и FCO равны как внутренние накрест лежащие при параллельных АВ, CD и секущей АС.
| + | <br> ''А. В. Погорелов, [http://xvatit.com/vuzi/ '''Геометрия'''] для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> |
| | | | |
| - | Из равенства треугольников следует равенство сторон: OE=OF, что и требовалось доказать.<br><br>
| |
| | | | |
| - | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br>
| |
| | | | |
| | <sub>Планирование уроков по математике [[Гипермаркет знаний - первый в мире!|онлайн]], задачи и ответы по классам, домашнее задание по математике 8 класса [[Математика|скачать]]</sub> | | <sub>Планирование уроков по математике [[Гипермаркет знаний - первый в мире!|онлайн]], задачи и ответы по классам, домашнее задание по математике 8 класса [[Математика|скачать]]</sub> |
| Строка 32: |
Строка 32: |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | '''<u></u>''' | | '''<u></u>''' |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Доказательство. Пусть ABCD — данный параллелограмм (рис. 120). Проведем его диагональ BD. Отметим на ней середину О и на продолжении отрезка АО отложим отрезок ОС1, равный АО.
Из равенства треугольников следует равенство сторон: OE=OF, что и требовалось доказать.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.