|
|
|
| Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Определение декартовых координат</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Определение декартовых координат, плоскости, координаты, параллельную, отрезок</metakeywords> |
| | | | |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика: Определение декартовых координат''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика: Определение декартовых координат''' |
| Строка 5: |
Строка 5: |
| | <br> | | <br> |
| | | | |
| - | ''' ОПРЕДЕЛЕНИЕ ДЕКАРТОВЫХ КООРДИНАТ''' | + | '''Определение декартовых координат''' |
| | | | |
| - | <br>Проведем на плоскости через точку О две взаимно перпендикулярные прямые x и у — оси координат (рис. 170). Ось x (она обычно горизонтальная) называется осью абсцисс, а ось у — осью ординат. Точкой пересечения О — началом координат — каждая из осей разбивается на две полуоси. Условимся одну из них называть положительной, отмечая ее стрелкой, а другую — отрицательной. | + | <br>Проведем на [[Розв’язування задач на перпендикулярність прямої та площини|плоскости]] через точку О две взаимно перпендикулярные прямые x и у — оси координат (рис. 170). Ось x (она обычно горизонтальная) называется осью абсцисс, а ось у — осью ординат. Точкой пересечения О — началом координат — каждая из осей разбивается на две полуоси. Условимся одну из них называть положительной, отмечая ее стрелкой, а другую — отрицательной. |
| | | | |
| - | Каждой точке А плоскости мы сопоставим пару чисел — координаты точки — абсциссу (x) и ординату (у) по такому правилу. | + | Каждой точке А плоскости мы сопоставим пару чисел — [[Шкалы и координаты|координаты]] точки — абсциссу (x) и ординату (у) по такому правилу. |
| | | | |
| - | Через точку А проведем прямую, параллельную оси ординат (рис. 171). Она пересечет ось абсцисс х в некоторой точке А<sub>х</sub>. Абсциссой точки А мы будем называть число х, абсолютная величина которого равна расстоянию от точки О до точки Ах. Это число будет положительным, если Ах принадлежит положительной полуоси, и отрицательным, если А<sub>х</sub><br> <br>[[Image:22-06-94.jpg]]<br> <br>принадлежит отрицательной полуоси. Если точка А лежит на оси ординат у, то полагаем х равным нулю. | + | Через точку А проведем прямую, параллельную оси ординат (рис. 171). Она пересечет ось абсцисс х в некоторой точке А<sub>х</sub>. Абсциссой точки А мы будем называть число х, абсолютная величина которого равна расстоянию от точки О до точки Ах. Это число будет положительным, если Ах принадлежит положительной полуоси, и отрицательным, если А<sub>х</sub><br> <br>[[Image:22-06-94.jpg|480px|Определение декартовых координат]]<br> <br>принадлежит отрицательной полуоси. Если точка А лежит на оси ординат у, то полагаем х равным нулю. |
| | | | |
| - | Ордината (у) точки А определяется аналогично. Через точку А проведем прямую, параллельную оси абсцисс x (см. рис. 171). Она пересечет ось ординат у в некоторой точке A<sub>y</sub>. Ординатой точки А мы будем называть число у, абсолютная величина которого равна расстоянию от точки О до точки A<sub>y</sub>. Это число будет положительным, если А<sub>у</sub> принадлежит положительной полуоси,и отрицательным, если А<sub>у</sub> принадлежит отрицательной полуоси. Если точка А лежит на оси абсцисс x, то полагаем у равным нулю. | + | Ордината (у) точки А определяется аналогично. Через точку А проведем прямую, [[Признак параллельности прямых. Полные уроки|параллельную]] оси абсцисс x (см. рис. 171). Она пересечет ось ординат у в некоторой точке A<sub>y</sub>. Ординатой точки А мы будем называть число у, абсолютная величина которого равна расстоянию от точки О до точки A<sub>y</sub>. Это число будет положительным, если А<sub>у</sub> принадлежит положительной полуоси,и отрицательным, если А<sub>у</sub> принадлежит отрицательной полуоси. Если точка А лежит на оси абсцисс x, то полагаем у равным нулю. |
| | | | |
| - | Координаты точки будем записывать в скобках рядом с буквенным обозначением точки, например: А (х; у) (на первом месте абсцисса, на втором — ордината). | + | Координаты точки будем записывать в скобках рядом с буквенным обозначением точки, например: А (х; у) (на первом месте абсцисса, на втором — ордината).<br> |
| | | | |
| | + | [[Image:22-06-95.jpg|180px|Р. Декарт]]<br> |
| | | | |
| | + | Оси координат разбивают плоскость на четыре части — четверти: I, II, III, IV (рис. 172). В пределах одной четверти знаки обеих координат сохраняются и имеют значения, указанные на рисунке.<br> |
| | | | |
| - | [[Image:22-06-95.jpg]] | + | [[Image:22-06-96.jpg|180px|Определение декартовых координат]]<br> <br>Точки оси X (оси абсцисс) имеют равные нулю ординаты 9у = 0), а точки оси у (оси ординат) имеют равные нулю абсциссы (х=0). У начала координат абсцисса и ордината равны нулю. |
| | | | |
| | + | Плоскость, на которой введены описанным выше способом координаты х и у, будем называть плоскостью ху. Произвольную точку на этой плоскости с координатами XVI у будем иногда обозначать просто (х; у). Введенные на плоскости координаты xw.y называются декартовыми по имени Р. Декарта, который впервые применил их в своих исследованиях. |
| | | | |
| | + | Задача (9). Даны точки А ( — 3; 2) и В (4; 1). Докажите, что [[Отрезок. Полные уроки|отрезок]] АВ пересекает ось у, но не пересекает ось x. |
| | | | |
| - | Оси координат разбивают плоскость на четыре части — четверти: I, II, III, IV (рис. 172). В пределах одной четверти знаки обеих координат сохраняются и имеют значения, указанные на рисунке.
| + | Решение. Ось у разбивает плоскость ху на две полуплоскости. В одной полуплоскости абсциссы точек положительны, а в другой — отрицательны. Так как у точек А и В абсциссы противоположных знаков, то точки А и В лежат в разных полуплоскостях. А это значит, что отрезок АВ пересекает ось у. |
| | | | |
| | + | Ось x также разбивает плоскость ху на две полуплоскости. В одной полуплоскости ординаты точек положительны, а в другой — отрицательны. У точек А и В ординаты одного знака (положительны). Значит, точки А и В лежат в одной полуплоскости. А следовательно, отрезок АВ не пересекается с осью х. |
| | | | |
| | + | <br> ''А. В. Погорелов, [http://xvatit.com/vuzi/ Геометрия] для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> |
| | | | |
| - | [[Image:22-06-96.jpg]]<br> <br>Точки оси X (оси абсцисс) имеют равные нулю ординаты 9у = 0), а точки оси у (оси ординат) имеют равные нулю абсциссы (х=0). У начала координат абсцисса и ордината равны нулю.
| |
| | | | |
| - | Плоскость, на которой введены описанным выше способом координаты хну, будем называть плоскостью ху. Произвольную точку на этой плоскости с координатами XVI у будем иногда обозначать просто (х; у). Введенные на плоскости координаты xw.y называются декартовыми по имени Р. Декарта, который впервые применил их в своих исследованиях.
| |
| - |
| |
| - | Задача (9). Даны точки А ( — 3; 2) и В (4; 1). Докажите, что отрезок АВ пересекает ось у, но не пересекает ось x.
| |
| - |
| |
| - | Решение. Ось у разбивает плоскость ху на две полуплоскости. В одной полуплоскости абсциссы точек положительны, а в другой — отрицательны. Так как у точек А и В абсциссы противоположных знаков, то точки А и В лежат в разных полуплоскостях. А это значит, что отрезок АВ пересекает ось у.
| |
| - |
| |
| - | Ось x также разбивает плоскость ху на две полуплоскости. В одной полуплоскости ординаты точек положительны, а в другой — отрицательны. У точек А и В ординаты одного знака (положительны). Значит, точки А и В лежат в одной полуплоскости. А следовательно, отрезок АВ не пересекается с осью х.<br>
| |
| - |
| |
| - | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br>
| |
| | | | |
| | <sub>[[Гипермаркет знаний - первый в мире!|онлайн]] библиотека с учебниками и книгами, планы конспектов уроков по математике, задания по математике 8 класса [[Математика|скачать]]</sub> | | <sub>[[Гипермаркет знаний - первый в мире!|онлайн]] библиотека с учебниками и книгами, планы конспектов уроков по математике, задания по математике 8 класса [[Математика|скачать]]</sub> |
| Строка 44: |
Строка 40: |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | '''<u></u>''' | | '''<u></u>''' |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Текущая версия на 11:35, 9 октября 2012
Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика: Определение декартовых координат
Определение декартовых координат
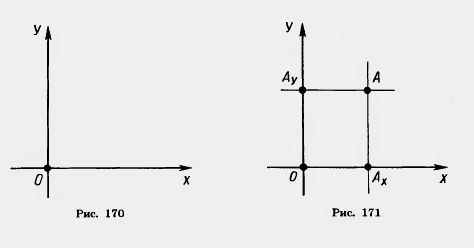
Проведем на плоскости через точку О две взаимно перпендикулярные прямые x и у — оси координат (рис. 170). Ось x (она обычно горизонтальная) называется осью абсцисс, а ось у — осью ординат. Точкой пересечения О — началом координат — каждая из осей разбивается на две полуоси. Условимся одну из них называть положительной, отмечая ее стрелкой, а другую — отрицательной.
Каждой точке А плоскости мы сопоставим пару чисел — координаты точки — абсциссу (x) и ординату (у) по такому правилу.
Через точку А проведем прямую, параллельную оси ординат (рис. 171). Она пересечет ось абсцисс х в некоторой точке Ах. Абсциссой точки А мы будем называть число х, абсолютная величина которого равна расстоянию от точки О до точки Ах. Это число будет положительным, если Ах принадлежит положительной полуоси, и отрицательным, если Ах
принадлежит отрицательной полуоси. Если точка А лежит на оси ординат у, то полагаем х равным нулю.
Ордината (у) точки А определяется аналогично. Через точку А проведем прямую, параллельную оси абсцисс x (см. рис. 171). Она пересечет ось ординат у в некоторой точке Ay. Ординатой точки А мы будем называть число у, абсолютная величина которого равна расстоянию от точки О до точки Ay. Это число будет положительным, если Ау принадлежит положительной полуоси,и отрицательным, если Ау принадлежит отрицательной полуоси. Если точка А лежит на оси абсцисс x, то полагаем у равным нулю.
Координаты точки будем записывать в скобках рядом с буквенным обозначением точки, например: А (х; у) (на первом месте абсцисса, на втором — ордината).

Оси координат разбивают плоскость на четыре части — четверти: I, II, III, IV (рис. 172). В пределах одной четверти знаки обеих координат сохраняются и имеют значения, указанные на рисунке.
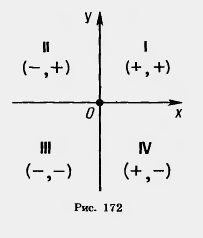
Точки оси X (оси абсцисс) имеют равные нулю ординаты 9у = 0), а точки оси у (оси ординат) имеют равные нулю абсциссы (х=0). У начала координат абсцисса и ордината равны нулю.
Плоскость, на которой введены описанным выше способом координаты х и у, будем называть плоскостью ху. Произвольную точку на этой плоскости с координатами XVI у будем иногда обозначать просто (х; у). Введенные на плоскости координаты xw.y называются декартовыми по имени Р. Декарта, который впервые применил их в своих исследованиях.
Задача (9). Даны точки А ( — 3; 2) и В (4; 1). Докажите, что отрезок АВ пересекает ось у, но не пересекает ось x.
Решение. Ось у разбивает плоскость ху на две полуплоскости. В одной полуплоскости абсциссы точек положительны, а в другой — отрицательны. Так как у точек А и В абсциссы противоположных знаков, то точки А и В лежат в разных полуплоскостях. А это значит, что отрезок АВ пересекает ось у.
Ось x также разбивает плоскость ху на две полуплоскости. В одной полуплоскости ординаты точек положительны, а в другой — отрицательны. У точек А и В ординаты одного знака (положительны). Значит, точки А и В лежат в одной полуплоскости. А следовательно, отрезок АВ не пересекается с осью х.
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
онлайн библиотека с учебниками и книгами, планы конспектов уроков по математике, задания по математике 8 класса скачать
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|













