|
|
| Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Расстояние между точками</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Расстояние между точками, плоскости, прямоугольному треугольнику, формула, точка</metakeywords> |
| | | | |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика: Расстояние между точками''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика: Расстояние между точками''' |
| | | | |
| - | <br>
| |
| | | | |
| - | '''РАССТОЯНИЕ МЕЖДУ ТОЧКАМИ'''
| + | '''Расстояние между точками''' |
| | | | |
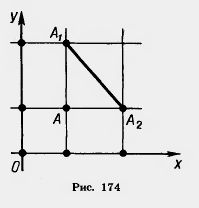
| - | <br>Пусть на плоскости ху даны две точки: А<sub>1</sub> с координатами x<sub>1</sub>, у1 к А<sub>2</sub> с координатами x<sub>2</sub>, у<sub>2</sub>. Выразим расстояние между точками A<sub>1</sub> и А<sub>2</sub> через координаты этих точек.<br> <br>Рассмотрим сначала случай, когда x<sub>1</sub>[[Image:22-06-97.jpg]]x<sub>2</sub> и у<sub>1</sub>[[Image:22-06-97.jpg]]у<sub>2</sub>- Проведем через точки А, и А<sub>2</sub> прямые, параллельные осям координат, и обозначим через А точку их пересечения (рис. 174). Расстояние между точками А и A<sub>1</sub> равно Iy<sub>1</sub> — y<sub>2</sub>I, а расстояние между точками А и А<sub>2</sub> равно Iх<sub>1</sub>—Х<sub>2</sub>I. Применяя к прямоугольному треугольнику А А<sub>1</sub>А <sub>2</sub> теорему Пифагора, получим:<br>d<sub>2</sub> = (x<sub>1</sub>—x<sub>2</sub>)<sup>2</sup> + (y<sub>1</sub> — y<sub>2</sub>)<sup>2</sup><br> | + | <br>Пусть на [[Урок 12. Плоские поверхности. Плоскость|плоскости]] ху даны две точки: А<sub>1</sub> с координатами x<sub>1</sub>, у1 к А<sub>2</sub> с координатами x<sub>2</sub>, у<sub>2</sub>. Выразим расстояние между точками A<sub>1</sub> и А<sub>2</sub> через координаты этих точек.<br> <br>Рассмотрим сначала случай, когда x<sub>1</sub>[[Image:22-06-97.jpg]]x<sub>2</sub> и у<sub>1</sub>[[Image:22-06-97.jpg]]у<sub>2</sub>- Проведем через точки А, и А<sub>2</sub> прямые, параллельные осям координат, и обозначим через А точку их пересечения (рис. 174). Расстояние между точками А и A<sub>1</sub> равно Iy<sub>1</sub> — y<sub>2</sub>I, а расстояние между точками А и А<sub>2</sub> равно Iх<sub>1</sub>—Х<sub>2</sub>I. Применяя к [[Співвідношення між сторонами і кутами прямокутного трикутника|прямоугольному треугольнику]] А А<sub>1</sub>А <sub>2</sub> теорему Пифагора, получим: |
| | | | |
| - | где d — расстояние между точками А<sub>1</sub> и А<sub>2</sub>. <br>
| + | d<sub>2</sub> = (x<sub>1</sub>—x<sub>2</sub>)<sup>2</sup> + (y<sub>1</sub> — y<sub>2</sub>)<sup>2</sup><br> |
| | | | |
| - | [[Image:22-06-103.jpg]]<br>
| + | где d — расстояние между точками А<sub>1</sub> и А<sub>2</sub>. <br> |
| | | | |
| - | <br>Хотя формула (*) для расстояния между точками выведена нами в предположении x<sub>1</sub> [[Image:22-06-97.jpg]]x<sub>2</sub>,у<sub>1</sub>[[Image:22-06-97.jpg]]у<sub>2</sub>, она остается верной и в других случаях. Действительно, если x<sub>1</sub>=x<sub>2</sub>, у<sub>1</sub>[[Image:22-06-97.jpg]]у<sub>2</sub>, то d равно Iу<sub>1</sub>—у<sub>2</sub>I Тот же результат дает и формула (*). Аналогично рассматривается случай, когда x<sub>1</sub>[[Image:22-06-97.jpg]]x<sub>2</sub>, y<sub>1</sub>=y<sub>2</sub>, При x<sub>1</sub> = x<sub>2</sub>, y<sub>1</sub>=y<sub>2</sub> точки А<sub>1</sub> и А<sub>2</sub> совпадают и формула (*) дает d=0. | + | [[Image:22-06-103.jpg|240px|Расстояние между точками]]<br>Хотя формула (*) для расстояния между точками выведена нами в предположении x<sub>1</sub> [[Image:22-06-97.jpg]]x<sub>2</sub>,у<sub>1</sub>[[Image:22-06-97.jpg]]у<sub>2</sub>, она остается верной и в других случаях. Действительно, если x<sub>1</sub>=x<sub>2</sub>, у<sub>1</sub>[[Image:22-06-97.jpg]]у<sub>2</sub>, то d равно Iу<sub>1</sub>—у<sub>2</sub>I Тот же результат дает и формула (*). Аналогично рассматривается случай, когда x<sub>1</sub>[[Image:22-06-97.jpg]]x<sub>2</sub>, y<sub>1</sub>=y<sub>2</sub>, При x<sub>1</sub> = x<sub>2</sub>, y<sub>1</sub>=y<sub>2</sub> точки А<sub>1</sub> и А<sub>2</sub> совпадают и [[Конспект уроку на тему «Формула коренів квадратного рівняння»|формула]] (*) дает d=0. |
| | | | |
| - | Задача (19). Найдите на оси х точку, равноудаленную от точек (1; 2) и (2; 3). | + | '''Задача (19).''' Найдите на оси х точку, равноудаленную от точек (1; 2) и (2; 3). |
| | | | |
| - | Решение. Пусть (х; 0) — искомая точка. Приравнивая расстояния от нее до данных точек, получим: | + | '''Решение.''' Пусть (х; 0) — искомая точка. Приравнивая расстояния от нее до данных точек, получим: |
| | + | |
| | + | (x - 1)<sup>2</sup> + (0-2)<sup>2</sup>= (x-2)<sup>2</sup> + (0-3)<sup>2</sup>. Отсюда находим x = 4. Значит, искомая [[Точка, пряма, площина. Промінь. Відрізок. Презентація уроку|точка]] есть (4; 0). <br> |
| | + | |
| | + | <br> ''А. В. Погорелов, [http://xvatit.com/vuzi/ Геометрия] для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> |
| | | | |
| - | (x - 1)<sup>2</sup> + (0-2)<sup>2</sup>= (x-2)<sup>2</sup> + (0-3)<sup>2</sup>. Отсюда находим x = 4. Значит, искомая точка есть (4; 0).<br> <br>
| |
| | | | |
| - | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br>
| |
| | | | |
| | <sub>Календарно-тематическое планирование по математике, задачи и ответы школьнику [[Гипермаркет знаний - первый в мире!|онлайн]], курсы учителю по математике [[Математика|скачать]]</sub> | | <sub>Календарно-тематическое планирование по математике, задачи и ответы школьнику [[Гипермаркет знаний - первый в мире!|онлайн]], курсы учителю по математике [[Математика|скачать]]</sub> |
| Строка 28: |
Строка 29: |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | '''<u></u>''' | | '''<u></u>''' |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.