|
|
| Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Симметрия относительно точки</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Симметрия относительно точки, точка, симметричная, фигуры, треугольники</metakeywords> |
| | | | |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика: Симметрия относительно точки''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика: Симметрия относительно точки''' |
| Строка 5: |
Строка 5: |
| | <br> | | <br> |
| | | | |
| - | '''СИММЕТРИЯ ОТНОСИТЕЛЬНО ТОЧКИ'''<br>
| + | '''Симметрия относительно точки'''<br> |
| | | | |
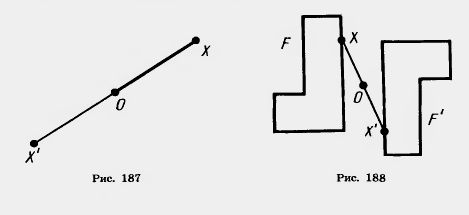
| - | <br>Пусть О — фиксированная точка и X — произвольная точка плоскости (рис. 187). Отложим на продолжении отрезка ОХ за точку О отрезок ОХ', равный ОХ. | + | <br>Пусть О — фиксированная [[Точка и прямая|точка]] и X — произвольная точка плоскости (рис. 187). Отложим на продолжении отрезка ОХ за точку О отрезок ОХ', равный ОХ. |
| | | | |
| - | Точка X' называется симметричной точке X относительно точки О. Точка, симметричная точке О, есть сама точка О. Очевидно, что точка, симметричная точке X', есть точка X.<br> | + | Точка X' называется симметричной точке X относительно точки О. Точка, [[Презентація уроку: Симетрія відносно точки. Симетрія відносно прямої|симметричная]] точке О, есть сама точка О. Очевидно, что точка, симметричная точке X', есть точка X.<br> |
| | | | |
| - | Преобразование фигуры F в фигуру F', при котором каждая ее точка X переходит в точку X', симметричную относительно данной точки О, называется '''''преобразованием симметрии относительно точки О'''''. При этом фигуры F и F' называются '''''симметричными относительно точки О''''' (рис. 188).<br> | + | Преобразование фигуры F в фигуру F', при котором каждая ее точка X переходит в точку X', симметричную относительно данной точки О, называется преобразованием симметрии относительно точки О. При этом [[Геометрические фигуры|фигуры]] F и F' называются симметричными относительно точки О (рис. 188).<br> |
| | | | |
| - | <br> | + | [[Image:22-06-139.jpg|480px|Симметрия относительно точки]]<br> |
| | | | |
| - | [[Image:22-06-139.jpg]]<br>
| + | Если преобразование симметрии относительно точки О переводит фигуру F в себя, то она называется центрально-симметричной, а точка О называется центром симметрии.<br> |
| | | | |
| - | <br> | + | Например, параллелограмм является центрально-симметричной фигурой. Его центром симметрии является точка пересечения диагоналей (рис. 189).<br><br>[[Image:22-06-140.jpg|480px|Симметрия относительно точки]]<br> <br>'''Теорема 9.2. '''Преобразование симметрии относительно точки является движением.<br> |
| | | | |
| - | Если преобразование симметрии относительно точки О переводит фигуру F в себя, то она называется '''''центрально-симметричной''''', а точка О называется '''''центром симметрии.'''''<br>
| + | '''Доказательство'''. Пусть X и Y — две произвольные точки фигуры F (рис. 190). Преобразование симметрии относительно точки О переводит их в точки X' и У. <br> |
| | | | |
| - | Например, параллелограмм является центрально-симметричной фигурой. Его центром симметрии является точка пересечения диагоналей (рис. 189).<br><br>[[Image:22-06-140.jpg]]<br> <br>Теорема 9.2. '''''Преобразование симметрии относительно точки является движением.'''''<br>
| + | Рассмотрим треугольники XOY и X'OY'. Эти [[Треугольник. Полные уроки|треугольники]] равны по первому признаку равенства треугольников. У них углы при вершине О равны как вертикальные, а ОХ=ОХ', OY=OY' по определению симметрии относительно точки О. Из равенства треугольников следует равенство сторон: XY=X'Y'. А это значит, что симметрия относительно точки О есть движение. Теорема доказана. |
| | | | |
| - | Доказательство. Пусть X и Y — две произвольные точки фигуры F (рис. 190). Преобразование симметрии относительно точки О переводит их в точки X' и У. <br>
| + | <br> ''А. В. Погорелов, [http://xvatit.com/vuzi/ Геометрия] для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> |
| | | | |
| - | Рассмотрим треугольники XOY и X'OY'. Эти треугольники равны по первому признаку равенства треугольников. У них углы при вершине О равны как вертикальные, а ОХ=ОХ', OY=OY' по определению симметрии относительно точки О. Из равенства треугольников следует равенство сторон: XY=X'Y'. А это значит, что симметрия относительно точки О есть движение. Теорема доказана.<br><br>
| |
| | | | |
| - | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br>
| |
| | | | |
| | <sub>Математика [[Математика|скачать]], задача школьнику 8 класса, материалы по математике для 8 класса [[Гипермаркет знаний - первый в мире!|онлайн]]</sub> | | <sub>Математика [[Математика|скачать]], задача школьнику 8 класса, материалы по математике для 8 класса [[Гипермаркет знаний - первый в мире!|онлайн]]</sub> |
| Строка 34: |
Строка 32: |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | '''<u></u>''' | | '''<u></u>''' |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Преобразование фигуры F в фигуру F', при котором каждая ее точка X переходит в точку X', симметричную относительно данной точки О, называется преобразованием симметрии относительно точки О. При этом фигуры F и F' называются симметричными относительно точки О (рис. 188).
Если преобразование симметрии относительно точки О переводит фигуру F в себя, то она называется центрально-симметричной, а точка О называется центром симметрии.
Например, параллелограмм является центрально-симметричной фигурой. Его центром симметрии является точка пересечения диагоналей (рис. 189).
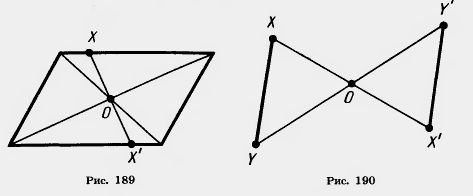
Теорема 9.2. Преобразование симметрии относительно точки является движением.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.