|
|
|
| Строка 1: |
Строка 1: |
| - | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Равенство фигур</metakeywords> | + | <metakeywords>Гипермаркет Знаний - первый в мире!, Гипермаркет Знаний, Математика, 8 класс, Алгебра, урок, на Тему, Равенство фигур, фигуры, треугольников, углы, симметрии, перпендикулярна</metakeywords> |
| | | | |
| | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика: Равенство фигур''' | | '''[[Гипермаркет знаний - первый в мире!|Гипермаркет знаний]]>>[[Математика|Математика]]>>[[Математика 8 класс|Математика 8 класс]]>>Математика: Равенство фигур''' |
| Строка 5: |
Строка 5: |
| | <br> | | <br> |
| | | | |
| - | ''' РАВЕНСТВО ФИГУР'''<br> | + | '''Равенство фигур'''<br> |
| | | | |
| - | <br>'''''Две фигуры называются равными, если они движением переводятся одна в другую.''''' | + | <br>Две [[Урок 39. Пересечение геометрических фигур|фигуры]] называются равными, если они движением переводятся одна в другую. |
| | | | |
| - | Для обозначения равенства фигур используется обычный знак равенства. Запись F=F' означает, что фигура F равна фигуре F'. В записи равенства треугольников: [[Image:21-06-11.jpg]]АВС= [[Image:21-06-11.jpg]]А<sub>1</sub>В<sub>1</sub>C<sub>1</sub> — предполагается, что совмещаемые при движении вершины стоят на соответствующих местах. При таком условии равенство треугольников, определяемое через их совмещение движением, и равенство, как мы его понимали до сих пор, выражают одно и то же.<br> | + | Для обозначения равенства фигур используется обычный знак равенства. Запись F=F' означает, что фигура F равна фигуре F'. В записи равенства треугольников: [[Image:21-06-11.jpg]]АВС= [[Image:21-06-11.jpg]]А<sub>1</sub>В<sub>1</sub>C<sub>1</sub> — предполагается, что совмещаемые при движении вершины стоят на соответствующих местах. При таком условии равенство [[Отрезок. Длина отрезка. Треугольник|треугольников]], определяемое через их совмещение движением, и равенство, как мы его понимали до сих пор, выражают одно и то же.<br> |
| | | | |
| - | <br> | + | [[Image:22-06-154.jpg|480px|Равенство фигур]]<br> |
| | | | |
| - | [[Image:22-06-154.jpg]]<br> | + | Это значит, что если у двух треугольников соответствующие стороны равны и соответствующие углы равны, то эти треугольники совмещаются движением. И обратно: если два треугольника совмещаются движением, то у них соответствующие стороны равны и соответствующие [[Внешние углы треугольника. Полные уроки|углы]] равны. Докажем оба эти утверждения.<br> |
| | | | |
| - | <br> | + | Пусть треугольник АBС совмещается движением с треугольником А<sub>1</sub>В<sub>1</sub>С<sub>1</sub>, причем вершина А переходит в вершину А<sub>1</sub>, B —В<sub>1</sub> и С — C<sub>1</sub>. Так как при движении сохраняются расстояния и углы, то для наших треугольников АВ=А<sub>1</sub>В<sub>1</sub>, BС=В<sub>1</sub>С<sub>1</sub>, АС=А<sub>1</sub>С<sub>1</sub> [[Image:20-06-61.jpg]]A=[[Image:20-06-61.jpg]]A<sub>1</sub> [[Image:20-06-61.jpg]]B= [[Image:20-06-61.jpg]]B<sub>1</sub> [[Image:20-06-61.jpg]]C= [[Image:20-06-61.jpg]]C<sub>1</sub>. |
| | | | |
| - | Это значит, что если у двух треугольников соответствующие стороны равны и соответствующие углы равны, то эти треугольники совмещаются движением. И обратно: если два треугольника совмещаются движением, то у них соответствующие стороны равны и соответствующие углы равны. Докажем оба эти утверждения.<br>
| + | Пусть теперь у треугольников АИС и А<sub>1</sub>В<sub>1</sub>C <sub>1</sub>, АБ=А<sub>1</sub>В<sub>1</sub>, ВС=В<sub>1</sub>С<sub>1 </sub>и АС=>АС=А<sub>1</sub>С<sub>1</sub>, [[Image:20-06-61.jpg]]A = [[Image:20-06-61.jpg]]A<sub>1</sub>,[[Image:20-06-61.jpg]]B= [[Image:20-06-61.jpg]]B<sub>1</sub>, [[Image:20-06-61.jpg]]C= [[Image:20-06-61.jpg]]C<sub>1</sub>. Докажем, что они совмещаются движением, причем вершина А переходит в вершину А<sub>1</sub>, B — в В<sub>1</sub>, С — в С<sub>1</sub>. Подвергнем треугольник АBС преобразованию [[Презентація уроку: Симетрія відносно точки. Симетрія відносно прямої|симметрии]] относительно прямой a, перпендикулярной к отрезку АА<sub>1</sub> и проходящей через его середину (рис. 206). Получим треугольник А<sub>1</sub>В<sub>2</sub>С<sub>2</sub>. Если точки B<sub>1</sub> и B<sub>2</sub> различны, то подвергнем его симметрии относительно прямой b, которая проходит через точку А<sub>1</sub> и [[Шпаргалки на тему «Паралельні та перпендикулярні прямі, їх властивості. Доведення від супротивного»|перпендикулярна]] |
| | + | к прямой В<sub>1</sub>В<sub>2</sub>. Получим треугольник А<sub>1</sub>В<sub>1</sub>C<sub>3</sub>. |
| | | | |
| - | Пусть треугольник АBС совмещается движением с треугольником А<sub>1</sub>В<sub>1</sub>С<sub>1</sub>, причем вершина А переходит в вершину А<sub>1</sub>, B —В<sub>1</sub> и С — C<sub>1</sub>. Так как при движении сохраняются расстояния и углы, то для наших треугольников АВ=А<sub>1</sub>В<sub>1</sub>, BС=В<sub>1</sub>С<sub>1</sub>, АС=А<sub>1</sub>С<sub>1</sub> [[Image:20-06-61.jpg]]A=[[Image:20-06-61.jpg]]A<sub>1</sub> [[Image:20-06-61.jpg]]B= [[Image:20-06-61.jpg]]B<sub>1</sub> [[Image:20-06-61.jpg]]C= [[Image:20-06-61.jpg]]C<sub>1</sub>.<br>
| + | Если точки С<sub>1</sub> и Сз лежат по одну сторону от прямой А<sub>1</sub>В<sub>1</sub>, то они совпадают. Действительно, так как углы В<sub>1</sub>А<sub>1</sub>С<sub>1</sub> и В<sub>1</sub>А<sub>1</sub>Сз, равны, то лучи А<sub>1</sub>С<sub>1</sub> и А<sub>1</sub>С<sub>3</sub> совпадают, а так как отрезки А<sub>1</sub>С<sub>1</sub> и А<sub>1</sub> С<sub>3</sub> равны, то совпадают точки С<sub>1</sub> и Сз. Таким образом, треугольник ABC движением переведен в треугольник А<sub>1</sub>В<sub>1</sub>С<sub>1</sub>. |
| | | | |
| - | <br>Пусть теперь у треугольников АИС и А<sub>1</sub>В<sub>1</sub>C <sub>1</sub>, АБ=А<sub>1</sub>В<sub>1</sub>, ВС=В<sub>1</sub>С<sub>1 </sub>и АС=>АС=А<sub>1</sub>С<sub>1</sub>, [[Image:20-06-61.jpg]]A = [[Image:20-06-61.jpg]]A<sub>1</sub>,[[Image:20-06-61.jpg]]B= [[Image:20-06-61.jpg]]B<sub>1</sub>, [[Image:20-06-61.jpg]]C= [[Image:20-06-61.jpg]]C<sub>1</sub>. Докажем, что они совмещаются движением, причем вершина А переходит в вершину А<sub>1</sub>, B — в В<sub>1</sub>, С — в С<sub>1</sub>. Подвергнем треугольник АBС преобразованию симметрии относительно прямой a, перпендикулярной к отрезку АА<sub>1</sub> и проходящей через его середину (рис. 206). Получим треугольник А<sub>1</sub>В<sub>2</sub>С<sub>2</sub><sub></sub>. Если точки B<sub>1</sub> и B<sub>2</sub> различны, то подвергнем его симметрии относительно прямой b, которая проходит через точку А<sub>1</sub> и перпендикулярна к прямой В<sub>1</sub>В<sub>2</sub>. Получим треугольник<br>А<sub>1</sub>В<sub>1</sub>C<sub>3</sub>.
| + | Если точки С<sub>1</sub> и Сз лежат по разные стороны от прямой А<sub>1</sub>В<sub>1</sub>, то для доказательства надо еще применить симметрию относительно прямой А<sub>1</sub>В<sub>1</sub>.<br> |
| | + | |
| | + | <br> ''А. В. Погорелов, [http://xvatit.com/vuzi/ Геометрия] для 7-11 классов, Учебник для общеобразовательных учреждений'' <br> |
| | | | |
| - | Если точки С<sub>1</sub> и Сз лежат по одну сторону от прямой А<sub>1</sub>В<sub>1</sub>, то они совпадают. Действительно, так как углы В<sub>1</sub>А<sub>1</sub>С<sub>1</sub> и В<sub>1</sub>А<sub>1</sub>Сз, равны, то лучи А<sub>1</sub>С<sub>1</sub> и А<sub>1</sub>С<sub>3</sub> совпадают, а так как отрезки А<sub>1</sub>С<sub>1</sub> и А<sub>1</sub> С<sub>3</sub> равны, то совпадают точки С<sub>1</sub> и Сз. Таким образом, треугольник ABC движением переведен в треугольник А<sub>1</sub>В<sub>1</sub>С<sub>1</sub>.<br>Если точки С<sub>1</sub> и Сз лежат по разные стороны от прямой А<sub>1</sub>В<sub>1</sub>, то для доказательства надо еще применить симметрию относительно прямой А<sub>1</sub>В<sub>1</sub>.<br><br>
| |
| | | | |
| - | <br> ''А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений'' <br>
| |
| | | | |
| | <sub>Планирование по математике , учебники и книги [[Гипермаркет знаний - первый в мире!|онлайн]], курсы и задачи по математике для 8 класса [[Математика|скачать]]</sub> | | <sub>Планирование по математике , учебники и книги [[Гипермаркет знаний - первый в мире!|онлайн]], курсы и задачи по математике для 8 класса [[Математика|скачать]]</sub> |
| Строка 32: |
Строка 33: |
| | | | |
| | '''<u>Содержание урока</u>''' | | '''<u>Содержание урока</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] конспект урока ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] конспект урока ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] опорный каркас | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] опорный каркас |
| - | [[Image:1236084776 kr.jpg|10x10px]] презентация урока | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] презентация урока |
| - | [[Image:1236084776 kr.jpg|10x10px]] акселеративные методы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] акселеративные методы |
| - | [[Image:1236084776 kr.jpg|10x10px]] интерактивные технологии | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] интерактивные технологии |
| | | | |
| | '''<u>Практика</u>''' | | '''<u>Практика</u>''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] задачи и упражнения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] задачи и упражнения |
| - | [[Image:1236084776 kr.jpg|10x10px]] самопроверка | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] самопроверка |
| - | [[Image:1236084776 kr.jpg|10x10px]] практикумы, тренинги, кейсы, квесты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] практикумы, тренинги, кейсы, квесты |
| - | [[Image:1236084776 kr.jpg|10x10px]] домашние задания | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] домашние задания |
| - | [[Image:1236084776 kr.jpg|10x10px]] дискуссионные вопросы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] дискуссионные вопросы |
| - | [[Image:1236084776 kr.jpg|10x10px]] риторические вопросы от учеников | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] риторические вопросы от учеников |
| - |
| + | |
| | '''<u>Иллюстрации</u>''' | | '''<u>Иллюстрации</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] аудио-, видеоклипы и мультимедиа ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] аудио-, видеоклипы и мультимедиа ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] фотографии, картинки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фотографии, картинки |
| - | [[Image:1236084776 kr.jpg|10x10px]] графики, таблицы, схемы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] графики, таблицы, схемы |
| - | [[Image:1236084776 kr.jpg|10x10px]] юмор, анекдоты, приколы, комиксы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] юмор, анекдоты, приколы, комиксы |
| - | [[Image:1236084776 kr.jpg|10x10px]] притчи, поговорки, кроссворды, цитаты | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] притчи, поговорки, кроссворды, цитаты |
| | | | |
| | '''<u>Дополнения</u>''' | | '''<u>Дополнения</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] рефераты''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] рефераты''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] статьи | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] статьи |
| - | [[Image:1236084776 kr.jpg|10x10px]] фишки для любознательных | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] фишки для любознательных |
| - | [[Image:1236084776 kr.jpg|10x10px]] шпаргалки | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] шпаргалки |
| - | [[Image:1236084776 kr.jpg|10x10px]] учебники основные и дополнительные | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] учебники основные и дополнительные |
| - | [[Image:1236084776 kr.jpg|10x10px]] словарь терминов | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] словарь терминов |
| - | [[Image:1236084776 kr.jpg|10x10px]] прочие | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] прочие |
| | '''<u></u>''' | | '''<u></u>''' |
| | <u>Совершенствование учебников и уроков | | <u>Совершенствование учебников и уроков |
| - | </u>'''[[Image:1236084776 kr.jpg|10x10px]] исправление ошибок в учебнике''' | + | </u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] исправление ошибок в учебнике''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] обновление фрагмента в учебнике | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обновление фрагмента в учебнике |
| - | [[Image:1236084776 kr.jpg|10x10px]] элементы новаторства на уроке | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] элементы новаторства на уроке |
| - | [[Image:1236084776 kr.jpg|10x10px]] замена устаревших знаний новыми | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] замена устаревших знаний новыми |
| - |
| + | |
| | '''<u>Только для учителей</u>''' | | '''<u>Только для учителей</u>''' |
| - | <u></u>'''[[Image:1236084776 kr.jpg|10x10px]] идеальные уроки ''' | + | <u></u>'''[[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] идеальные уроки ''' |
| - | [[Image:1236084776 kr.jpg|10x10px]] календарный план на год | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] календарный план на год |
| - | [[Image:1236084776 kr.jpg|10x10px]] методические рекомендации | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] методические рекомендации |
| - | [[Image:1236084776 kr.jpg|10x10px]] программы | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] программы |
| - | [[Image:1236084776 kr.jpg|10x10px]] обсуждения | + | [[Image:1236084776 kr.jpg|10x10px|1236084776 kr.jpg]] обсуждения |
| | | | |
| | | | |
Текущая версия на 14:41, 9 октября 2012
Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика: Равенство фигур
Равенство фигур
Две фигуры называются равными, если они движением переводятся одна в другую.
Для обозначения равенства фигур используется обычный знак равенства. Запись F=F' означает, что фигура F равна фигуре F'. В записи равенства треугольников:  АВС= АВС=  А1В1C1 — предполагается, что совмещаемые при движении вершины стоят на соответствующих местах. При таком условии равенство треугольников, определяемое через их совмещение движением, и равенство, как мы его понимали до сих пор, выражают одно и то же. А1В1C1 — предполагается, что совмещаемые при движении вершины стоят на соответствующих местах. При таком условии равенство треугольников, определяемое через их совмещение движением, и равенство, как мы его понимали до сих пор, выражают одно и то же.
Это значит, что если у двух треугольников соответствующие стороны равны и соответствующие углы равны, то эти треугольники совмещаются движением. И обратно: если два треугольника совмещаются движением, то у них соответствующие стороны равны и соответствующие углы равны. Докажем оба эти утверждения.
Пусть треугольник АBС совмещается движением с треугольником А1В1С1, причем вершина А переходит в вершину А1, B —В1 и С — C1. Так как при движении сохраняются расстояния и углы, то для наших треугольников АВ=А1В1, BС=В1С1, АС=А1С1  A= A= A1 A1  B= B=  B1 B1  C= C=  C1. C1.
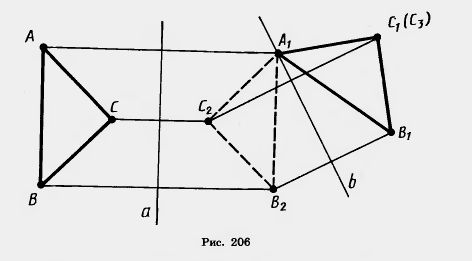
Пусть теперь у треугольников АИС и А1В1C 1, АБ=А1В1, ВС=В1С1 и АС=>АС=А1С1,  A = A =  A1, A1, B= B=  B1, B1,  C= C=  C1. Докажем, что они совмещаются движением, причем вершина А переходит в вершину А1, B — в В1, С — в С1. Подвергнем треугольник АBС преобразованию симметрии относительно прямой a, перпендикулярной к отрезку АА1 и проходящей через его середину (рис. 206). Получим треугольник А1В2С2. Если точки B1 и B2 различны, то подвергнем его симметрии относительно прямой b, которая проходит через точку А1 и перпендикулярна
к прямой В1В2. Получим треугольник А1В1C3. C1. Докажем, что они совмещаются движением, причем вершина А переходит в вершину А1, B — в В1, С — в С1. Подвергнем треугольник АBС преобразованию симметрии относительно прямой a, перпендикулярной к отрезку АА1 и проходящей через его середину (рис. 206). Получим треугольник А1В2С2. Если точки B1 и B2 различны, то подвергнем его симметрии относительно прямой b, которая проходит через точку А1 и перпендикулярна
к прямой В1В2. Получим треугольник А1В1C3.
Если точки С1 и Сз лежат по одну сторону от прямой А1В1, то они совпадают. Действительно, так как углы В1А1С1 и В1А1Сз, равны, то лучи А1С1 и А1С3 совпадают, а так как отрезки А1С1 и А1 С3 равны, то совпадают точки С1 и Сз. Таким образом, треугольник ABC движением переведен в треугольник А1В1С1.
Если точки С1 и Сз лежат по разные стороны от прямой А1В1, то для доказательства надо еще применить симметрию относительно прямой А1В1.
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Планирование по математике , учебники и книги онлайн, курсы и задачи по математике для 8 класса скачать
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|











